Анализ строения конечных групп

Рассмотрим группы вращений правильных многоугольников. Если Р_m-правильный m-многоугольник, то рассматривается совокупность всех вращений и всех осевых симметрий, переводящих многоугольник P_m в себя.

Указанные преобразования можно рассматривать как подстановки множества вершин многоугольника Р_m.

Группа диэдра правильного треугольника. Имеется три вращения на углы

1, 2, 3 (рис.1.а) и три симметрии относительно трёх осей симметрий правильного треугольника (рис.1.б), переводящих правильный треугольник в себя.

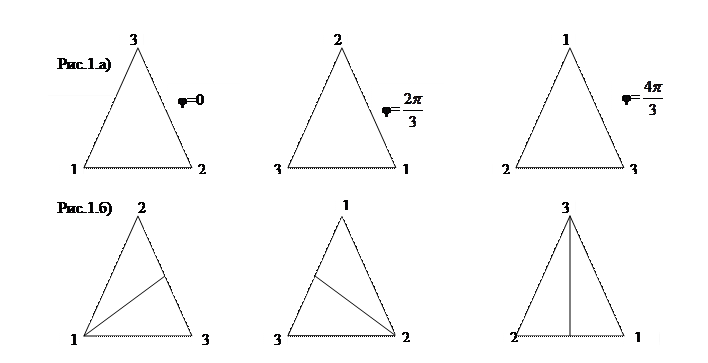
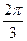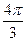Вращение на угол 1 определяет тождественную подстановку вершин, вращения на и определяют подстановки (1 2 3) и (1 3 2) соответственно. Далее, три возможные симметрии определяют три транспозиции (2 3), (1 3),(1 2).Указанными шестью подстановками исчерпываются всевозможные подстановки множества вершин треугольника. Пусть для определённости, а₁=Е=е, а₂=(1 2 3), а₃=(1 3 2),

а₄=(2 3),а₅=(1 3),а₆=(1 2).

Обозначим а₁=е=1, а₂=(123)=а, а₃=( 132)=а², а₆=(12)=в. Тогда ав=а₄=(23), а²в=а₅=(13), ва=а₅=(13), в²=а³=е. Таким образом, элементами 1, а, а², в, аb, а²b исчерпываются элементы рассматриваемой группы. Все они записываются как произведение степеней элементов а, b, они называются образующими элементами. И в данном случае образуют симметрическую группу шестого порядка.

Симметрическая группа третьей степени

S₃= {е, а, а², в, аb, а²b};

Генетический код группы: а³=b²=е, bа=а²b.

Таблица 1 - Таблица Кэли элементов группы S₃

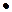	е	a2	a	b	ab	a2b
е	е	a2	a	b	ab	a2b
a	a	е	a2	ab	a2b	b
a2	a2	a	е	a2b	b	ab
b	b	a2b	ab	е	a	a2
a2b	a2b	ab	b	a2	е	a
ab	ab	b	a2b	a	a2	е

Таблица 2 - Таблица сопряжения элементов группы S_3.

*	е	a2	a	b	ab	a2b
е	е	е	е	е	е	е
a	a	a	a	a2	a2	a2
a2	a2	a2	a2	a	a	a
b	b	a2b	ab	b	a2b	a2
ab	ab	b	a2b	a2b	ab	b
a2b	a2b	ab	b	ab	b	a2b

Классы сопряженных элементов группы S₃.

{е}; {a, a²}; {b, ab, a²b}.

Пример заполнения таблицы 1: а 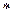а=а², bа²=bаа=а²bа=а² а² b= а³аb= еаb=аb

Докажем, что это группа:

1. Замкнутость, аа=а²; аb²b=а² и т.д.

2. Ассоциотивность, (аbb) а=а², аb(bа)=аbа²b=а².

3. Наличие нейтрального элемента-е

4. Наличие для каждого обратного элемента (симметричного) элемента ,аа²=е, а²bа²b=е.

1. Подгруппы группы S₃ .

H₀={е}; H₁={е, a, a²}; H₂₌{е, b}; H₃={е, ab}; H₄={е, a²b}; H₅=S₃

2.Смежные классы и индекс подгруппы H группы S₃ .

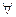а 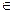S₃ aH_i i=0, е,…5.

H₁-S₃= {е, a, a²} {b, ab, a²b}, 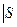₃ : H₁ 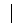=2

H₂-S₃={е, b} {a, a²b} {a², ab}, 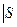_{3 :} H₂ 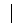=3

H₃-S₃={е, ab} {b, a²} {a, a²b}, 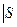₃ : H₃ =3

H₄-S₃= {е, a²b} {a, b} {a², ab}, 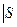₄ : H =3

Классы сопряженных элементов.

a^G={a, a²}; b^G={b, ab, a²b}, е^G={е}

Коммутатор.

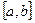= а^-1 b^-1 ab = а¹ a^b

Коммутатор а-{е, a}; a²-{е, a²}; b-{е, a, a²}; ab-{е, a, a²}; a²b-{е, a, _a2}.Таким образом, получаем, что 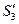={е, a, a²} – коммутант группы S₃.

Таблица 3 - Таблица коммутаторирования элементов группы S_3.