Прямоугольная декартова система координат в пространстве
КРАТКИЙ СПРАВОЧНИК ПО МАТЕМАТИКЕ
ФОРМУЛЫ И ТЕОРЕМЫ АЛГЕБРЫ И НАЧАЛА АНАЛИЗА
Степени и корни
Свойства степеней
Для любых 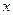 ,
, 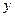 и
и 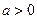 и
и 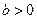 верны равенства:
верны равенства: 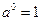 ;
; 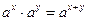 ;
; 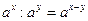 ;
;  ;
; 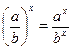 ;
; 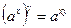 ;
; 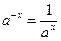 .
.
Формулы сокращённого умножения
Для любых 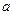 ,
, 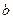 и
и 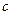 верны равенства:
верны равенства:
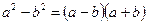 ;
; 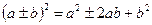 ;
; 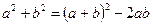 ;
; 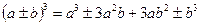 ;
; 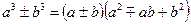 ;
; 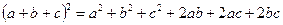 ;
;
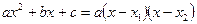 , где
, где 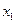 и
и 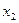 – корни уравнения
– корни уравнения 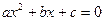 .
.
Свойства арифметических корней
Для любых натуральных 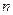 и
и 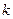 , больших 1, и любых неотрицательных
, больших 1, и любых неотрицательных 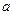 и
и 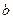 верны равенства:
верны равенства: 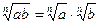 ;
; 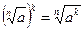 ;
; 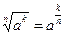 ;
; 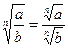 ,
, 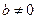 ;
; 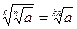 ;
; 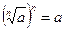 ;
; 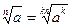 ;
; 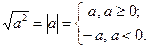
Неравенства
Свойства числовых неравенств
-
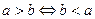 .
. -
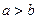 и
и 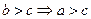 .
. -
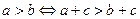 для любого числа
для любого числа 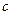 .
. -
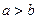 и
и 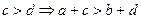 .
. -
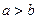 и
и 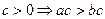 .
. -
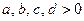 , причём
, причём 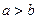 и
и 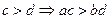 .
. -
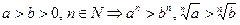 .
. -
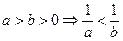 .
. -
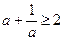 ;
; 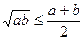 .
.
Свойства модулей
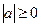 ;
; 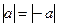 ;
; 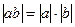 ;
; 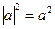 ;
; 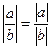 .
.
Решение уравнений
Линейное уравнение 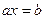 . Решение:
. Решение: 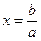
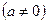 .
.
Квадратное уравнение 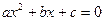 . Решение:
. Решение: 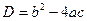 ;
; 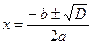 .
.
Теорема Виета: если 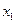 ,
, 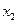 – корни квадратного уравнения
– корни квадратного уравнения 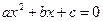 , то
, то 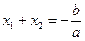 ;
; 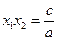 .
.
Прогрессии
Арифметическая прогрессия 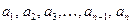 .
.
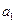 – первый член прогрессии;
– первый член прогрессии; 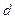 – разность;
– разность; 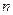 – число членов;
– число членов; 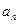 –
– 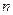 -й член прогрессии;
-й член прогрессии; 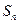 – сумма
– сумма 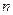 первых членов прогрессии;
первых членов прогрессии; 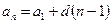 ;
; 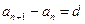 ;
; 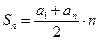 ;
; 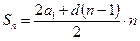 ;
; 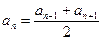 .
.
Геометрическая прогрессия 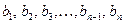 .
.
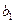 – первый член прогрессии;
– первый член прогрессии; 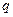 – знаменатель
– знаменатель 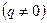 ;
; 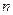 – число членов;
– число членов; 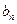 –
– 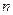 -й член прогрессии;
-й член прогрессии; 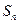 – сумма
– сумма 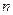 первых членов прогрессии;
первых членов прогрессии; 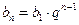 ;
; 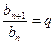 ;
; 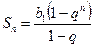 ,
, 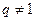 ;
; 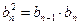 . Если
. Если 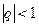 , то
, то 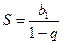 – сумма бесконечной геометрической прогрессии.
– сумма бесконечной геометрической прогрессии.
Тригонометрия
Зависимость между тригонометрическими функциями одного аргумента
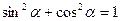 ;
; 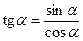 ,
, 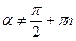 ;
; 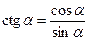 ,
, 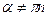 ;
; 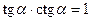 ,
, 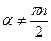 ;
; 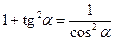 ;
; 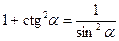 .
.
Формулы сложения (сумма и разность аргументов)
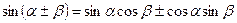 ;
; 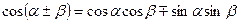 ;
; 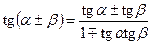 ;
; 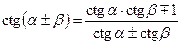 ;
;
Тригонометрические функции двойного аргумента
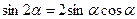 ;
; 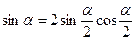 ;
; 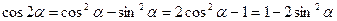 ;
; 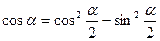 ;
; 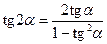 .
.
Тригонометрические функции половинного аргумента

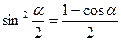 ;
; 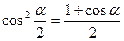 ;
; 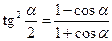 ;
; 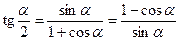 .
.
Преобразование суммы тригонометрических функций
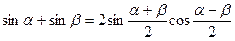 ;
; 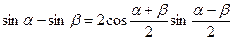 ;
; 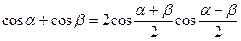 ;
; 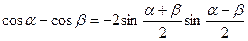 ;
; 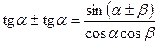 .
.
Преобразование произведения тригонометрических функций в сумму
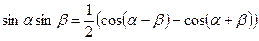 ;
; 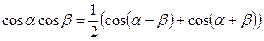 ;
; 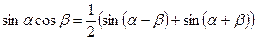 ;
; 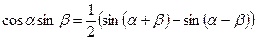 .
.
Выражение тригонометрических функций через тангенс половинного аргумента
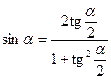 ;
; 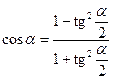 ;
; 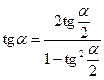 ;
; 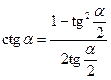 .
.
Формулы приведения
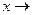 | 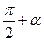 | 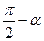 | 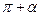 | 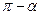 | 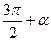 | 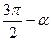 | 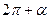 | 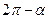 |
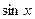 | 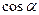 | 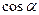 | 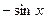 | 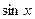 | 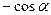 | 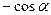 | 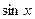 | 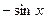 |
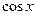 | 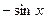 | 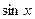 | 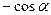 | 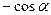 | 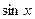 | 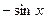 | 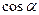 | 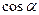 |
tg 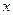 | 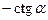 | 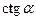 | 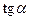 | 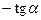 | 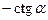 | 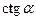 | 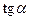 | 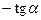 |
ctg 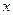 | 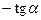 | 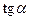 | 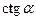 | 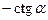 | 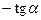 | 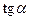 | 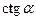 | 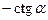 |
Связь между градусной и радианной мерами измерения угла: 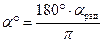 ;
; 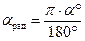
Простейшие тригонометрические уравнения
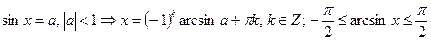 ;
; 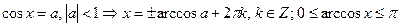 ;
; 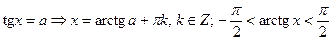 ;
; 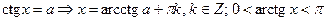 .
.
Частные случаи решения тригонометрических уравнений
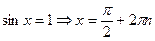 ;
; 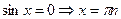 ;
; 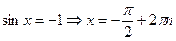 .
.
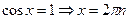 ;
; 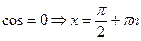 ;
; 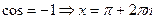 .
.
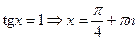 ;
; 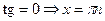 ;
; 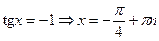 .
.
Обратные тригонометрические функции
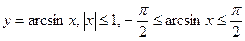 ;
; 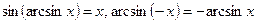 .
.
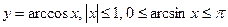 ;
; 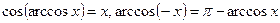 .
.
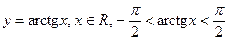 ;
; 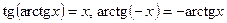 .
.
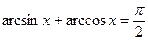 ;
; 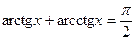 .
.
Логарифмы
Если 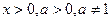 , то
, то 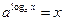 ;
; 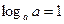 ;
; 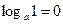 ;
; 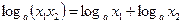 ;
; 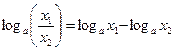 ;
; 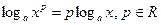 ;
; 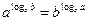 ;
; 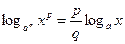 ;
; 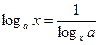 ;
; 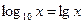 ;
; 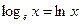 ; модуль перехода к новому основанию:
; модуль перехода к новому основанию: 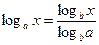 .
.
Производная
Правила дифференцирования
Пусть 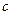 – постоянная, а
– постоянная, а 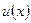 и
и 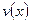 – дифференцируемые функции.
– дифференцируемые функции.
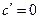 ;
; 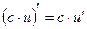 ;
; 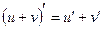 ;
; 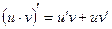 ;
; 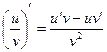 ;
; 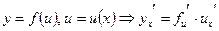 (производная сложной функции).
(производная сложной функции).
Таблица производных
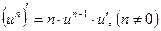 ;
; 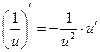 ;
; 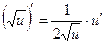 ;
; 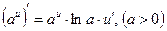 ;
; 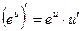 ;
; 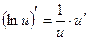 ;
; 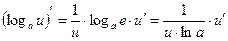 ;
; 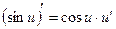 ;
; 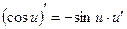 ;
; 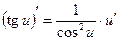 ;
; 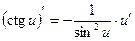 ;
; 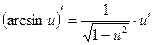 ;
; 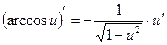 ;
; 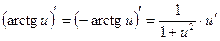 .
.
Уравнение касательной к графику функции 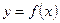 :
: 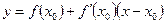 , где
, где 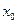 – абсцисса точки касания.
– абсцисса точки касания.
Векторы
Прямоугольная декартова система координат на плоскости
Расстояние между точками 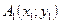 и
и 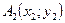 (длина вектора
(длина вектора 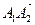 ):
): 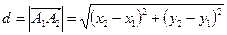 .
.
Координаты 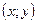 середины отрезка с концами
середины отрезка с концами 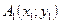 и
и 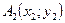 :
: 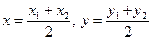 .
.
Общее уравнение прямой 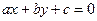 . Уравнение прямой с угловым коэффициентом и начальной ординатой имеет вид
. Уравнение прямой с угловым коэффициентом и начальной ординатой имеет вид 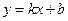 . Угловой коэффициент
. Угловой коэффициент 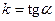 , где
, где 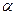 – угол, образованный прямой с положительным направлением оси Ох, а
– угол, образованный прямой с положительным направлением оси Ох, а 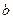 – значение ординаты точки пересечения прямой с осью Оу. Взаимное расположение прямых
– значение ординаты точки пересечения прямой с осью Оу. Взаимное расположение прямых 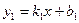 и
и 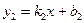 :
: 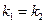 – условие параллельности прямых;
– условие параллельности прямых; 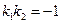 – условие перпендикулярности прямых.
– условие перпендикулярности прямых.
Уравнение окружности с радиусом 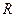 и с центром в точке
и с центром в точке 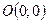
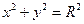 . Уравнение окружности с радиусом
. Уравнение окружности с радиусом 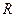 и с центром в точке
и с центром в точке 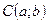
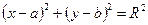 .
.
Прямоугольная декартова система координат в пространстве
Расстояние между точками 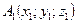 и
и 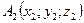 (длина вектора
(длина вектора 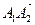 ):
): 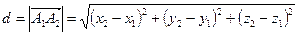 .
.
Модуль вектора 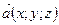 :
: 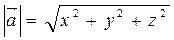 . Сложение векторов
. Сложение векторов 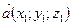 и
и 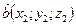 :
: 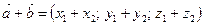 . Умножение вектора
. Умножение вектора 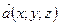 на число
на число 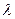 :
: 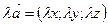 . Скалярное произведение векторов
. Скалярное произведение векторов 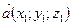 и
и 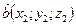 выражается формулой:
выражается формулой: 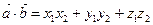 . Косинус угла между векторами
. Косинус угла между векторами 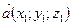 и
и 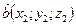 :
: 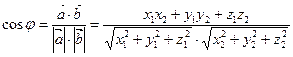 .
.
ФОРМУЛЫ И ТЕОРЕМЫ ПЛАНИМЕТРИИ
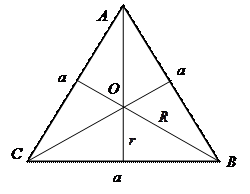
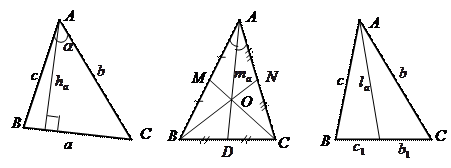 Произвольный треугольник
Произвольный треугольник
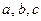 – стороны;
– стороны; 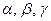 – противолежащие им углы;
– противолежащие им углы; 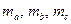 – медианы;
– медианы; 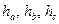 – высоты;
– высоты; 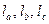 – биссектрисы;
– биссектрисы; 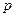 – полупериметр;
– полупериметр; 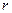 – радиус вписанной окружности;
– радиус вписанной окружности; 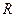 – радиус описанной окружности;
– радиус описанной окружности; 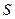 – площадь треугольника.
– площадь треугольника.
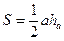 ;
; 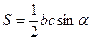 ;
; 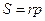 ;
; 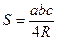 ;
; 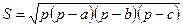 (формула Герона);
(формула Герона); 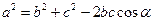 (теорема косинусов);
(теорема косинусов); 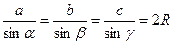 (теорема синусов);
(теорема синусов); 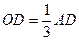 ,
, 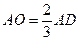 (свойство медиан треугольника);
(свойство медиан треугольника); 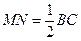 (средняя линия треугольника);
(средняя линия треугольника); 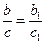 , где
, где 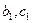 – отрезки, на которые биссектриса
– отрезки, на которые биссектриса 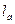 делит сторону
делит сторону 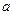 (свойство биссектрисы треугольника);
(свойство биссектрисы треугольника); 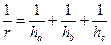 .
.
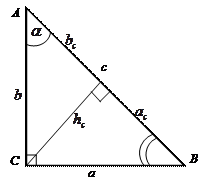 Прямоугольный треугольник
Прямоугольный треугольник
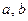 – катеты;
– катеты; 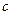 – гипотенуза;
– гипотенуза; 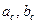 – проекции катетов на гипотенузу;
– проекции катетов на гипотенузу; 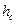 – высота;
– высота; 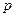 – полупериметр;
– полупериметр; 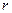 – радиус вписанной окружности;
– радиус вписанной окружности; 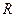 – радиус описанной окружности;
– радиус описанной окружности; 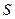 – площадь прямоугольного треугольника.
– площадь прямоугольного треугольника.
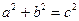 (теорема Пифагора);
(теорема Пифагора); 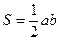 ;
; 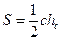 ;
; 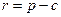 ;
; 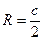 ;
; 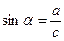 ;
; 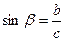 ;
; 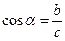 ;
; 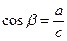 ;
; 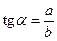 ;
; 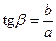 ,
, 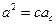 ;
; 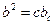 ;
; 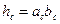 .
.
