Собственные значения и собственные векторы неотрицательных матриц.
Определение: Пусть L – заданное n- мерное линейное пространство. Ненулевой вектор 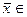 L называется собственным вектором линейного преобразования А, если существует такое число l, что выполняется равенство: A
L называется собственным вектором линейного преобразования А, если существует такое число l, что выполняется равенство: A 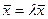 .
.
При этом число l называется собственным значением (характеристическим числом) линейного преобразования А, соответствующего вектору 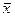 .
.
Определение: Если линейное преобразование А в некотором базисе 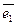 ,
, 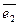 ,…,
,…, 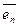 имеет матрицу А =
имеет матрицу А = 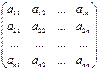 , то собственные значения линейного преобразования А можно найти как корни l1, l2, … ,ln уравнения:
, то собственные значения линейного преобразования А можно найти как корни l1, l2, … ,ln уравнения:
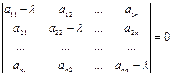
Это уравнение называется характеристическим уравнением, а его левая часть- характеристическим многочленом линейного преобразования А.
Следует отметить, что характеристический многочлен линейного преобразования не зависит от выбора базиса.
Рассмотрим частный случай. Пусть А – некоторое линейное преобразование плоскости, матрица которого равна 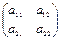 . Тогда преобразование А может быть задано формулами:
. Тогда преобразование А может быть задано формулами:
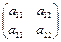
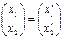 ;
; 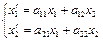 в некотором базисе
в некотором базисе 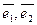 .
.
Если преобразование А имеет собственный вектор с собственным значением l, то А 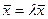 .
.
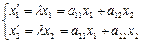 или
или 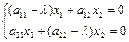
Т.к. собственный вектор 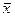 ненулевой, то х1 и х2 не равны нулю одновременно. Т.к. данная система однородна, то для того, чтобы она имела нетривиальное решение, определитель системы должен быть равен нулю. В противном случае по правилу Крамера система имеет единственное решение – нулевое, что невозможно.
ненулевой, то х1 и х2 не равны нулю одновременно. Т.к. данная система однородна, то для того, чтобы она имела нетривиальное решение, определитель системы должен быть равен нулю. В противном случае по правилу Крамера система имеет единственное решение – нулевое, что невозможно.
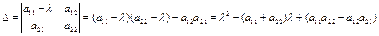
Полученное уравнение является характеристическим уравнением линейного преобразования А.
Таким образом, можно найти собственный вектор 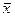 (х1, х2) линейного преобразования А с собственным значением l, где l - корень характеристического уравнения, а х1 и х2 – корни системы уравнений при подстановке в нее значения l.
(х1, х2) линейного преобразования А с собственным значением l, где l - корень характеристического уравнения, а х1 и х2 – корни системы уравнений при подстановке в нее значения l.
Понятно, что если характеристическое уравнение не имеет действительных корней, то линейное преобразование А не имеет собственных векторов.
Следует отметить, что если 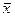 - собственный вектор преобразования А, то и любой вектор ему коллинеарный – тоже собственный с тем же самым собственным значением l.
- собственный вектор преобразования А, то и любой вектор ему коллинеарный – тоже собственный с тем же самым собственным значением l.
Действительно, 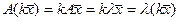 . Если учесть, что векторы имеют одно начало, то эти векторы образуют так называемое собственное направлениеили собственную прямую.
. Если учесть, что векторы имеют одно начало, то эти векторы образуют так называемое собственное направлениеили собственную прямую.
Т.к. характеристическое уравнение может иметь два различных действительных корня l1 и l2, то в этом случае при подстановке их в систему уравнений получим бесконечное количество решений. (Т.к. уравнения линейно зависимы). Это множество решений определяет две собственные прямые.
Если характеристическое уравнение имеет два равных корня l1 = l2 = l, то либо имеется лишь одна собственная прямая, либо, если при подстановке в систему она превращается в систему вида: 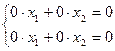 . Эта система удовлетворяет любым значениям х1 и х2. Тогда все векторы будут собственными, и такое преобразование называется преобразованием подобия.
. Эта система удовлетворяет любым значениям х1 и х2. Тогда все векторы будут собственными, и такое преобразование называется преобразованием подобия.
Рассмотрим другой частный случай. Если 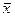 - собственный вектор линейного преобразования А, заданного в трехмерном линейном пространстве, а х1, х2, х3 – компоненты этого вектора в некотором базисе
- собственный вектор линейного преобразования А, заданного в трехмерном линейном пространстве, а х1, х2, х3 – компоненты этого вектора в некотором базисе 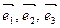 , то
, то 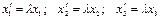 , где l - собственное значение (характеристическое число) преобразования А.
, где l - собственное значение (характеристическое число) преобразования А.
Если матрица линейного преобразования А имеет вид:
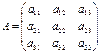 , то
, то 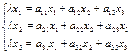
Характеристическое уравнение: 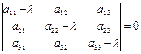
Раскрыв определитель, получим кубическое уравнение относительно l. Любое кубическое уравнение с действительными коэффициентами имеет либо один, либо три действительных корня.
