Построение диаграммы и полигона частот

Следующий этап первичной обработки – группирование и ее графическое представление. Группировка выборки объема n заключается в следующем: Промежуток [x_min, x_max] разбивают на m интервалов группирования (чаще всего одинаковой длины) и подсчитывают число n_j выборочных значений, которые попали в j-й интервал. Обычно выбирают m = 7 – 20, или рассчитывают по формуле

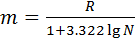. (8)

Kаждый интервал группировки Δ_j=(a_j, b_j) представлен своими левой a_j, и правой b_j границами и числом элементов выборки, которые принадлежат ему. Каждый интервал удобно представлять не двумя границами, а одним числом – средним значением.

Наиболее наглядная форма графического представления группирования – гистограмма. Если δ₁, δ₂,… δ_m – длины интервалов группирования, а 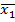, , 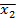,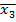.. 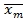– их середины и 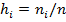– относительные частоты попадания наблюдений в j-й интервал группировки, то можно построить график ступенчатой функции: 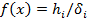, , 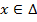j=l, 2,3.., m.

Этот график называется гистограммой. В Mathcad для построения гистограмм функции hist(Δ,ξ) hist(M,N,n) и histоgram(intvis,data).Для нашей задачи приемлемы функции hist(Δ,ξ) и histоgram(intvis,data).

Другая форма графического представления группируемых данных – полигон частот. Полигон частот – это ломаная линия, которая соединяет точки с координатами ( 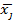, h_i) то есть с абсциссами, равными серединам интервалов группировки, и ординатами, равными соответствующим частотам.

Можно также построить полигон накопленных частот – график ломаной, соединяющей точки с координатами 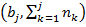, то есть с абсциссами, равными правым границам интервалов группирования и ординатами, равными соответствующим накопленным частотам или относительным накопленным частотам.

Ниже приведен фрагмент рабочего документа Mathcad с вычислением x_max, x_min и R=x_max–x_min для исследуемой выборки, а также с гистограммами и полигонами частот для разных интервалов группировки.

В Excel выборка разбивается на частоты с помощью встроенной функции ЧАСТОТА.

Она вычисляет частоту появления значений в определенном интервале и возвращает массив чисел. Поскольку данная функция возвращает массив, она должна задаваться как функция массива.

Синтаксис: ЧАСТОТА (массив данных; массив карманов (ячеек)), здесь: массив данных – это ссылка на массив данных, для которых вычисляются частоты. Если массив данных не содержит значений, то функция ЧАСТОТА возвращает массив нулей.

Массив карманов (ячеек) – это ссылка на массив интервалов, в которые группируются значения аргумента массива данных. Если массив карманов (ячеек) не содержит значений, то функция ЧАСТОТА возвращает количество элементов в аргументе массив данных. Гистограмма строится по массиву карманов (ячеек).

Из анализа выборочных характеристик, вида гистограммы (или полигона частот) высказывается нулевая гипотеза о виде закона распределения. Данная гипотеза требует проверки.