Теоретические сведения и примеры
Абсолютной величиной (модулем) 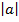 действительного числа а называется число а, если а положительно или равно нулю, и число –а, если а отрицательно.
действительного числа а называется число а, если а положительно или равно нулю, и число –а, если а отрицательно.
Иначе говоря, 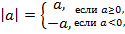 откуда
откуда 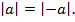
Абсолютную величину числа также можно определить как арифметический квадратный корень (т. е. положительное значение корня) из квадрата действительного числа 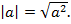 Удобно также вводить понятие абсолютной величины, рассматривая точки действительной числовой оси. Как известно, между всеми точками числовой оси и действительными числами существует взаимно-однозначное соответствие, т. е. каждому действительному числу соответствует ровно одна точка числовой оси, а каждой точке числовой оси соответствует ровно одно действительное число. Исходя из этого, можно определить абсолютную величину числа а как расстояние от начала отсчета (от точки ноль) до числа а на действительной оси.
Удобно также вводить понятие абсолютной величины, рассматривая точки действительной числовой оси. Как известно, между всеми точками числовой оси и действительными числами существует взаимно-однозначное соответствие, т. е. каждому действительному числу соответствует ровно одна точка числовой оси, а каждой точке числовой оси соответствует ровно одно действительное число. Исходя из этого, можно определить абсолютную величину числа а как расстояние от начала отсчета (от точки ноль) до числа а на действительной оси.
Решая уравнения, содержащие знак абсолютной величины, нужно учитывать все три определения и выбирать то, которое в данной ситуации приведет к ответу быстрее.
Пример 1. Решить уравнение 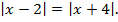
Решение. Воспользуемся определением абсолютной величины как арифметическим значением корня, тогда заданное уравнение можно переписать в виде :
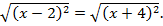
Возведем обе части в квадрат 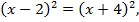 раскроем скобки и приведем подобные:
раскроем скобки и приведем подобные:
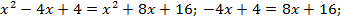
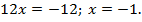
Поскольку возведение в квадрат обеих частей равенства может привести к появлению посторонних корней, то следует проверить, является ли найденное значение 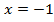 корнем исходного уравнения. Проверка показывает, что найденное значение удовлетворяет уравнению.
корнем исходного уравнения. Проверка показывает, что найденное значение удовлетворяет уравнению.
Ответ: 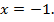
Замечание. При решении уравнения примера 1 можно было использовать геометрическое определение модуля.
Действительно, величина 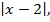 в силу определения, представляет собой расстояние между точками (х) и (2), а величина
в силу определения, представляет собой расстояние между точками (х) и (2), а величина 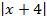 – расстояние между точками (х) и (–4). Таким образом, исходное уравнение имеет решением точку, находящуюся на действительной оси на одинаковом расстоянии от точек (–4) и (2). Иначе говоря, надо найти середину отрезка с конечными точками (–4) и (2). Следовательно,
– расстояние между точками (х) и (–4). Таким образом, исходное уравнение имеет решением точку, находящуюся на действительной оси на одинаковом расстоянии от точек (–4) и (2). Иначе говоря, надо найти середину отрезка с конечными точками (–4) и (2). Следовательно, 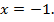
Пример 2. Решить уравнение 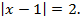
Решение. Поскольку модуль некоторого числа есть величина неотрицательная, то, по определению, либо 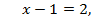 тогда
тогда 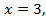 либо
либо 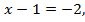 тогда
тогда 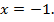
Ответ: данное уравнение имеет два корня 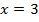 и
и 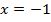 .
.
Пример 3. Решить уравнение 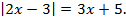
Решение. По определению, либо 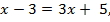 тогда
тогда 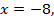 либо
либо 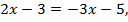 тогда
тогда 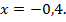
Проверка показывает, что при 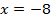 левая часть уравнения равна 19, а правая часть уравнения равна (–19). Поскольку
левая часть уравнения равна 19, а правая часть уравнения равна (–19). Поскольку 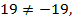 то значение
то значение 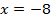 не является корнем уравнения. Подстановка значения
не является корнем уравнения. Подстановка значения 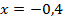 обращает исходное уравнение в тождество.
обращает исходное уравнение в тождество.
Ответ: х = – 0,4.
В более сложных случаях, когда уравнение не является линейным или содержит несколько знаков абсолютной величины, следует отдельно рассматривать каждый модуль, определяя, каким образом он будет раскрыт на том или ином множестве. Рекомендуется при решении уравнения, содержащего знак абсолютной величины, разбить область допустимых значений уравнения (ОДЗ) на множества, в каждом из которых выражения, стоящие под знаком модуля, сохраняют знак. На каждом таком множестве записать уравнение, раскрыв знак модуля, и решить на этом множестве. Объединение решений, найденных на всех частях ОДЗ уравнения, составляет множество всех решений уравнения.
В последующих примерах рассмотрим некоторые виды уравнений, содержащих знак модуля.
Уравнение вида 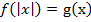 равносильно совокупности систем
равносильно совокупности систем 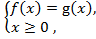 и
и 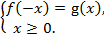
Пример 4. Решить уравнение 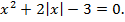
Решение. Исходное уравнение равносильно совокупности систем:
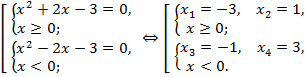
Для первой системы посторонним является значение 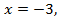 а для второй – значение
а для второй – значение 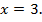 Таким образом, данное уравнение имеет два корня
Таким образом, данное уравнение имеет два корня 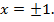
Ответ: 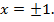
Замечание. В данном примере можно было воспользоваться свойством четности функции. Обозначим 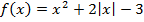 и примем во внимание, что
и примем во внимание, что 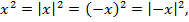 поэтому
поэтому 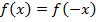 . Левая часть уравнения представляет собой четную функцию. Это означает, что если мы найдем корни при
. Левая часть уравнения представляет собой четную функцию. Это означает, что если мы найдем корни при 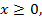 то решениями будут также числа, равные найденным корням по модулю, но с противоположным знаком.
то решениями будут также числа, равные найденным корням по модулю, но с противоположным знаком.
Если 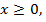 то уравнение принимает вид
то уравнение принимает вид 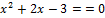 и
и 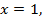 поскольку значение
поскольку значение 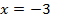 не удовлетворяет неравенству
не удовлетворяет неравенству 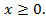
В силу четности функции 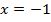 также будет решением равнения.
также будет решением равнения.
Ответ: 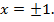
Уравнение вида 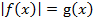 можно решить, исходя из условия, что либо
можно решить, исходя из условия, что либо 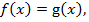 либо
либо 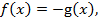 т. е., рассматривая совокупности систем:
т. е., рассматривая совокупности систем:
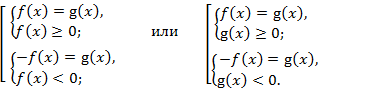
В примерах 2 и 3 приведены наиболее простые из уравнений подобного типа.
Заметим, что равенство 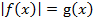 означает, что
означает, что 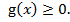
Пример 5. Найти все корни уравнения:
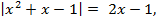 удовлетворяющие неравенству
удовлетворяющие неравенству 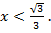
Решение. Данное уравнение равносильно совокупности систем:
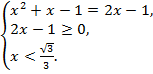 и
и 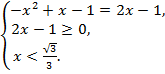
Решая каждую из систем в отдельности, получим:
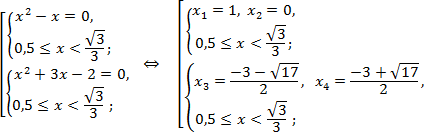 Только один корень
Только один корень 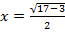 принадлежит промежутку
принадлежит промежутку 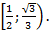
Ответ: 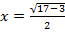 .
.
При решении уравнения, в котором под знаком модуля находится выражение, также содержащее модуль, следует сначала освободиться от внутренних модулей, а затем в полученных уравнениях раскрыть оставшиеся модули.
Пример 6. Решить уравнение:
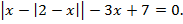
Решение. Исходное уравнение равносильно совокупности систем:
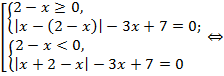
⇔ 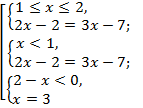 ⇔
⇔ 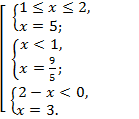
Единственным решением совокупности систем является значение х = 3.
Ответ: х = 3.
Уравнение вида 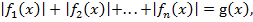 где
где 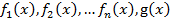 – некоторые функции, удобно решать методом интервалов. Для этого необходимо найти все точки, в которых хотя бы одна из функций меняет знак. Эти точки делят ОДЗ на промежутки, на каждом из которых все функции
– некоторые функции, удобно решать методом интервалов. Для этого необходимо найти все точки, в которых хотя бы одна из функций меняет знак. Эти точки делят ОДЗ на промежутки, на каждом из которых все функции 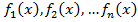 сохраняют знак. Затем, используя определение абсолютной величины, перейти от уравнения к совокупности систем, не содержащих знаков модуля.
сохраняют знак. Затем, используя определение абсолютной величины, перейти от уравнения к совокупности систем, не содержащих знаков модуля.
Пример 7.
Решить уравнение: 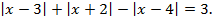
Решение. Находим интервалы знакопостоянства выражений 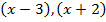 и
и 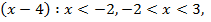
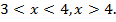 Таким образом, уравнение равносильно совокупности четырех систем:
Таким образом, уравнение равносильно совокупности четырех систем:
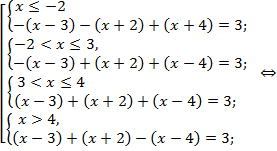
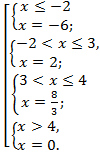
Вторая и третья системы не имеют решения. Решениями исходного уравнения являются числа 2 и –6.
Ответ: x = 2 и x = –6.
Замечание. Можно, решая пример 7, для наглядности рассмотреть числовую ось и соответствующие промежутки.
Согласно определению,
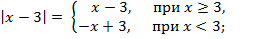
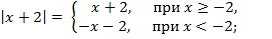
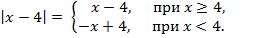
Получается, что на действительной оси следует выделить четыре промежутка: 
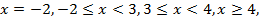
на каждом из которых знаки модулей раскрываются различным образом. Начертим числовую ось и укажем знаки раскрытия модулей на промежутках (рис. 3.1).
|
| |
| |
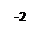

Рис. 3.1. Числовая ось, знаки раскрытия модулей на промежутках.
Найдем решение на каждом из промежутков.
Если 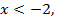 то все три модуля раскрываются с противоположным знаком:
то все три модуля раскрываются с противоположным знаком:
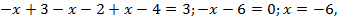 что удовлетворяет неравенству
что удовлетворяет неравенству 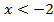 .
.
Если 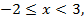 то
то 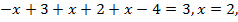 что соответствует неравенству
что соответствует неравенству 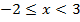 .
.
Если 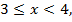 то
то 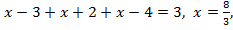 что не удовлетворяет неравенству
что не удовлетворяет неравенству 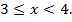
Если 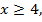 то
то 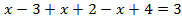 ,
, 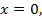 что не входит в область
что не входит в область 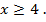 Следовательно, как и было указано ранее, решениями являются
Следовательно, как и было указано ранее, решениями являются 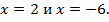 В сущности, мы повторили рассуждения, которые проводились в примере 7, но только добавили наглядности. Читатель может выбирать тот подход к решению, который ему удобнее.
В сущности, мы повторили рассуждения, которые проводились в примере 7, но только добавили наглядности. Читатель может выбирать тот подход к решению, который ему удобнее.
При решении неравенств, содержащих знак абсолютной величины, следует разбить область допустимых значений неравенства на множества, на каждом из которых выражения, стоящие под знаком модуля, сохраняют знак. На каждом таком множестве нужно решать неравенство и полученные решения объединять в множество решений исходного неравенства. Этот подход уже был продемонстрирован в примере 7.
Пример 8. Решить неравенство 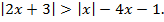
Решение. Точки х = –1,5и х = 0 делят числовую ось на три промежутка: 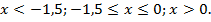 Решим данное неравенство на каждом из этих промежутков.
Решим данное неравенство на каждом из этих промежутков.
Если 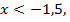 то неравенство имеет вид
то неравенство имеет вид
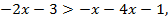 или 3х < 2, т. е.
или 3х < 2, т. е. 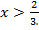 Следовательно, на данном промежутке неравенство решения не имеет.
Следовательно, на данном промежутке неравенство решения не имеет.
Если 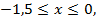 то
то 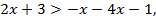 или
или 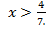 Таким образом,
Таким образом, 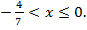
Если 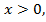 то
то 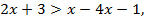 или
или 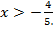 В этом случае решениями неравенства являются все положительные числа.
В этом случае решениями неравенства являются все положительные числа.
Объединяя найденные решения неравенства на всех частях ОДЗ, получаем 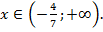
Ответ: 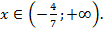
Пример 9. Решить неравенство:
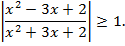
Решение. Данное неравенство равносильно объединению решений двух неравенств:
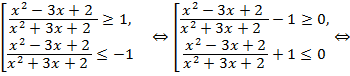
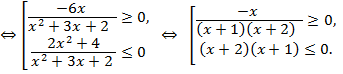
Методом интервалов находим решение первого неравенства, состоящее из объединения двух промежутков 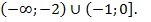 Решением второго неравенства является промежуток (–2; –1). Объединение этих множеств составляет решение исходного неравенства, т. е.
Решением второго неравенства является промежуток (–2; –1). Объединение этих множеств составляет решение исходного неравенства, т. е. 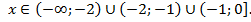
Ответ: 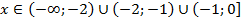 .
.
