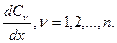Линейные неоднородные дифференциальные уравнения порядка выше 1-го с постоянными коэффициентами. Метод вариации постоянных

Доказано, что для линейного неоднородного дифференциального уравнения
y⁽ⁿ⁾ + a₁ y^(n-1) + ... + a_n-1 y' + a_n y = f(x)
при непрерывной правой части f(x), для любых начальных значений
x₀, y₀, y_0,1, ..., y_0,n-1
существует и единственно решение задачи Коши
y(x₀)=y₀, (y)'(x₀)=y_0,1 , ...,(y)^(n-1)(x₀)=y_0,n-1.

Решение задачи Коши для неоднородного дифференциального уравнения с постоянными коэффициентами можно найти методом вариации произвольных постоянных (методом Лагранжа), который состоит в следующем:
Записываем искомое решение задачи Коши для неоднородного уравнения в виде
y(x)= c₁(x) y₁(x) + c₂(x) y₂(x) + ... + c_n(x) y_n(x),
где y₁(x), y₂(x), ..., y_n(x) — линейно независимые решения соответствующего однородного уравнения, и находим неизвестные функции
c₁(x) , c₂(x), ..., c_n(x),
такие, чтобы функция y = y(x) удовлетворяла неоднородному уравнению и заданным начальным условиям.

Опишем алгоритм решения задачи Коши для уравнения второго порядка
y'' + a₁ y' + a₂ y = f(x), y(x₀)=y₀, (y)'(x₀)=y_0,1.
Будем искать решение задачи в виде
y(x)= c₁(x) y₁(x) + c₂(x) y₂(x),
где y₁(x), y₂(x) — линейно независимые решения однородного уравнения
y'' + a₁ y' + a₂ y = 0.
Вычислим y'(x), y''(x) и подставим полученные выражения в уравнение.
Вычислим первую производную
y'(x)= (c₁'(x) y₁(x) + c₂(x)' y₂(x)) + (c₁(x) y₁'(x) + c₂(x) y₂'(x)),
положим
c₁'(x) y₁(x) + c₂(x)' y₂(x) = 0
и тогда
y'(x)= c₁(x) y₁'(x) + c₂(x) y₂'(x),
y''(x)= (y'(x))'= (c₁(x) y₁'(x) + c₂(x) y₂'(x))'=
=c₁'(x) y₁'(x) + c₂(x)' y₂'(x) + c₁(x) y₁''(x) + c₂(x) y₂''(x).

Подставив y(x) и ее производные в уравнение, получим:
y'' + a₁ y' + a₂ y =
= c₁'(x) y₁'(x) + c₂(x)' y₂'(x) + c₁(x) y₁''(x) + c₂(x) y₂''(x) +
+ a₁(c₁(x) y₁'(x)+c₂(x) y₂'(x)) + a₂(c₁(x) y₁(x)+c₂(x) y₂(x)) =
= c₁(x)( y₁''(x)+a₁ y₁'(x)+a₂ y₁(x)) + c₂(x)( y₂''(x)+a₁ y₂'(x)+a₂ y₂(x)) +
+ c₁'(x) y₁'(x) + c₂(x)' y₂'(x) = 0 + 0 + c₁'(x) y₁'(x) + c₂(x)' y₂'(x) = f(x),
при условии c₁'(x) y₁(x) + c₂(x)' y₂(x) = 0.

Тогда неизвестные функции c₁(x) и c₂(x) являются решениями системы линейных дифференциальных уравнений
c₁'(x) y₁'(x) + c₂(x)' y₂'(x) = f(x),
c₁'(x) y₁(x) + c₂(x)' y₂(x) = 0
с известными y₁(x) и y₂(x).
Эта система легко разрешима относительно c₁(x) и c₂(x):
c₁'(x) = f(x)y₂(x)/(y₁'(x)y₂(x)-y₁(x)y₂'(x)),
c₁'(x)= f(x)y₁(x)/(y₁(x)y₂'(x)-y₁'(x)y₂(x)).
Вычислив интегралы в правой части системы, получим

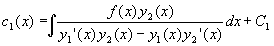
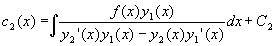
Произвольные константы C₁ и C₂ определяются из начальных условий.

Заметим, что разрешимость системы дифференциальных уравнений для
c₁'(x) и c₂'(x) и однозначная разрешимость системы начальных условий для произвольных констант C₁ и C₂ гарантированы линейной независимостью y₁(x) и y₂(x),
(y₁'(x)y₂(x)-y₁(x)y₂'(x))№0 для линейно независимых y₁(x) и y₂(x).

Для того чтобы решить задачу Коши для уравнения более высокого порядка действуем аналогично.
Решение задачи Коши ищем в виде
y(x)= c₁(x) y₁(x) + c₂(x) y₂(x) + ... + c_n(x) y_n(x),
где y₁(x), y₂(x), ..., y_n(x) — линейно независимые решения соответствующего однородного уравнения.
Неизвестные функции c₁(x) , c₂(x), ..., c_n(x)
находим как решения линейной системы дифференциальных уравнений
c₁'(x) y₁(x) + c₂(x)' y₂(x) + ... + c_n'(x) y_n(x) = 0
c₁'(x) y₁'(x) + c₂'(x) y₂'(x) + ... + c_n'(x) y_n'(x) = 0,
c₁'(x) y₁''(x) + c₂'(x) y₂''(x) + ... + c_n'(x) y_n''(x) = 0,
.................
c₁'(x) y₁^(n-1)(x) + c₂'(x) y₂^(n-1)(x) + ... + c_n'(x) y_n^(n-1)(x) = f(x),
которая в силу линейной независимости y₁(x), y₂(x), ..., y_n(x) разрешима относительно c_i'(x).
Вычислив c_i(x) = F_i(x) + C_i находим произвольные постоянные C_i из начальных условий и тогда искомое решение уравнения имеет вид
y(x)= F₁(x) y₁(x) + F₂(x) y₂(x) + ...+ F_n(x) y_n(x) + C₁y₁(x) + C₂ y₂(x) +...+ C_ny_n(x).

Таким образом, для того чтобы решить методом вариации произвольных постоянных решение задачи Коши для линейного неоднородного дифференциального уравнения с постоянными коэффициентами следует:
записать характеристическое уравнение;
найти все корни характеристического уравнения λ₁,λ ₂, ... , λ_n;
найти фундаментальную систему решений y₁(x), y₂(x), ..., y_n(x));
представить искомое решение задачи Коши в виде линейной комбинации
y(x)= c₁(x)y₁(x) + c₂(x)y₂(x) + ... + c_n(x)y_n(x),
с неизвестными функциями c₁(x), c₂(x), ..., c_n(x);
составить и решить систему для c₁ (x), c₂(x), ..., c_n(x);
подставить вычисленные c_i(x) = F_i(x) + C_i в выражение для решения и записать для него начальные условия;
найти из начальных условий значения констант C_i и записать искомое решение.

Для отыскания общего решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами следует
найти общее решение соответствующего однородного уравнения (записать характеристическое уравнение, найти все корни характеристического уравнения λ₁,λ₂, ... , λ_n, записать фундаментальную систему решений y₁(x), y₂(x), ..., y_n(x));
найти методом вариации произвольных постоянных любое частное решение неоднородного уравнения y_ч(x);
записать выражение для общего решения
y(x)= c₁ y₁(x) + c₂ y₂(x) + ... + c_n y_n(x) + y_ч(x).

Если известно общее решение 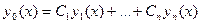, соответствующего уравнению (1) однородного уравнения , то для определения частного решения 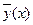уравнения (1) используют метод Лагранжа вариации произвольных постоянных.Именно , ищут частное решение неоднородного уравнения (1) в виде 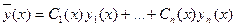, где от функций 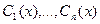дополнительно требуется,чтобы они удовлетворяли условиям 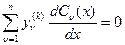для всех 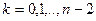(где 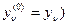.Тогда дляфункций 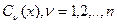,получимсистемууравнений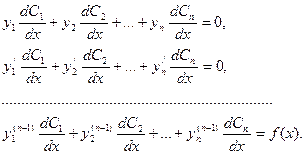

Определитель этой системы есть отличный от нуля вронскиан фундаментальной системы решений 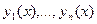,поэтому система имеет единственное решение относительно