Раздел 2. Аналитическая геометрия
ФИЛИАЛ В Г. РОСТОВЕ-НА-ДОНУ
ЛИНЕЙНАЯ АЛГЕБРА
Направление подготовки:
080100.62 «ЭКОНОМИКА»
Профили:
«ФИНАНСЫ И КРЕДИТ»
«БУХГАЛТЕРСКИЙ УЧЁТ, АНАЛИЗ И АУДИТ»
Квалификация (степень) выпускника:
«БАКАЛАВР»
Ростов-на-Дону – 2014 г.
Раздел 1. Линейная и векторная алгебра
I. Задания для самостоятельной работы
1. Изучить теоретический материал по теме «матрицы и определители»:
1.1. Матрицы, действия с ними.
1.2. Понятие обратной матрицы.
1.3. Матричная запись системы линейных уравнений.
1.4. Определители второго и третьего порядков, их свойства.
1.5. Алгебраические дополнения и миноры.
1.6. Определители n-го порядка. Вычисление определителя разложением по строке (столбцу).
1.7. Свойства определителей.
1.8. Вычисление обратной матрицы.
2. Изучить теоретический материал по теме «системы линейных алгебраических уравнений:
2.1. Системы трех линейных уравнений.
2.2. Правило Крамера.
2.3. Система n линейных уравнений с n неизвестными.
2.4. Метод Гаусса.
2.5. Метод обратной матрицы.
3. Изучить теоретический материал по теме «Пространство Rn»
3.1. Пространство Rn.
3.2. Линейные операции над векторами.
3.3. Норма в Rn.
3.4. Скалярное произведение в Rn.
3.5. Линейно зависимая и линейно независимая система векторов.
3.6. Условие компланарности трёх векторов в R3.
3.7. Угол между векторами
3.8. Базис.
4. Выполнить задания:
Задача 1
Даны матрицы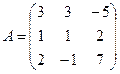 
, 
, 
.
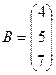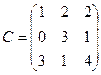1. Вычислить матрицу 4A+5C+7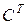 
.
2. Выполняется ли равенство AC=CA?
3. Вычислить определители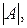 
, 
, 
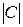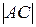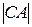и проверить равенство: = = 
.
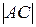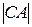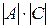4. Используя свойства определителей, вычислить определитель
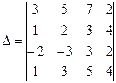
Задача 2
1. Решить систему AX=B матричным методом.
2. Решить системы уравнений по формулам Крамера:
, 
, 
.
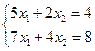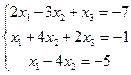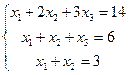3. Решить систему уравнений методом Гаусса: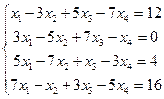 
.
Задача 3.Даны векторы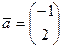 
, 
= 
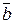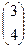. Вычислить и изобразить в системе координат следующие линейные комбинации векторов 
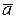и :
, 
, 
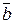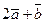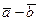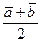
Задача 4
Найти линейную комбинацию векторов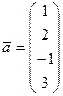 
, = 
, 
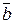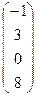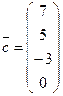с коэффициентами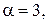 
.
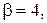
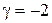Задача 5
Будут ли векторы линейно зависимы или линейно независимы в случаях:
а) =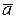 
= 
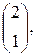
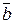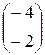; б) = 
= 
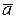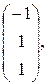
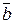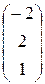; в) = = ,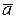 
?
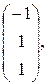
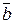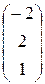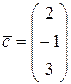Задача 6
Даны три вектора 
= 
= 
, 
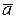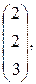
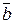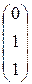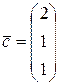. Доказать, что система 
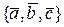образует базис в 
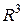. Найти разложение вектора 
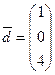по этому базису.
Задача 7.Даны два вектора = 
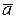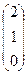и =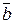 
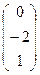. Найти 
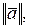угол 
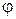между векторам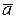и и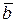 
, а также 
.
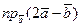Задача 8.При каком значении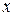 
вектор = 
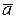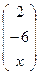ортогонален вектору = 
?
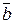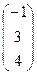При каких значениях x и y векторы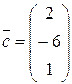 
и 
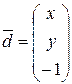параллельны?
Задача 9
Вычислить площадь и высоту треугольника с вершинами A(7;3;4), B(1;0;6) и C(4;5;7).
Задача 10
Вершины треугольной пирамиды находятся в точках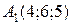 
, 
, 
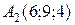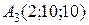и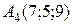 
. Вычислить: а) объем пирамиды; б) высоту, опущенную из вершины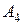 
Задача 11
Выяснить, лежат ли точки D(1;0;1), E(0;1;–3)в плоскости ABC, где A(5;–3;0), B(–4;3;3), C(–4;2;4).
II. Контрольные вопросы для самопроверки
1. Что называют матрицей?
2. Как определяются сумма матриц, умножение матрицы на действительное число?
3. Какие матрицы можно перемножать и каким образом?
4. Что такое невырожденная матрица?
5. Как вычислить определитель второго, третьего порядков?
6. Как найти обратную матрицу для данной вырожденной квадратной матрицы?
7. Что такое ранг матрицы?
8. В чем заключается правило Крамера для решения линейных систем?
9. Как с помощью обратной матрицы решить систему линейных уравнений?
10. Для решения каких систем применим метод обратной матрицы?
11. Для решения каких систем применяют метод Гаусса?
12. Что такое прямой и обратный ход метода Гаусса?
13. Как определяется скалярное произведение в пространстве Rn?
14. Как определяется норма в Rn?
15. Какие векторы называются линейно зависимыми?
16. Какие векторы в Rn образуют базис?
17. В чем состоит критерий базисности?
18. Как определить угол между векторами в Rn?
Раздел 2. Аналитическая геометрия
I. Задания для самостоятельной работы
1. Изучить теоретический материал по теме«Прямая в R2 и R3. Плоскость в R3» по вопросам:
1.1. Уравнения плоскости и прямой в пространстве.
1.2. Угол между плоскостями.
1.3. Угол между прямыми.
1.4. Угол между прямой и плоскостью.
1.5. Уравнение линии на плоскости.
1.6. Различные формы уравнения прямой на плоскости.
1.7. Угол между прямыми.
1.8. Расстояние от точки до прямой.
1.9. Взаимное расположение прямой и плоскости.
1.10. Расстояние от точки до плоскости.
2. Изучить теоретический материал по теме «Кривые и поверхности 2-го порядка» по вопросам:
2.1. Кривые второго порядка: окружность, эллипс, гипербола, парабола, их геометрические свойства и уравнения.
2.2. Полярная система координат.
2.3. Поверхности второго порядка: сфера, эллипсоид, гиперболоиды, конусы, цилиндры, параболоиды.
3. Выполнить задания:
Задача 1
а) Найти параметрические уравнения прямой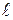 
, проходящей через точку 
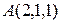параллельно вектору 
.
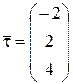б) При каком значении параметра t точка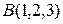 
принадлежит этой прямой?
в) Принадлежит ли точка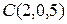 
этой прямой?
г) Построить данную прямую.
Задача 2
а) Составить параметрические уравнения прямой 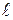, проходящей через точк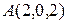и 
и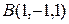 
.
б) Используя параметр, найти координаты точек C и D, делящих отрезок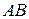 
на три равные части.
Задача 3
Построить плоскости и указать особенности их расположения:
а)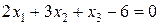 
;
б)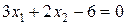 
;
в)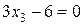 
;
г)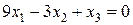 
;
д)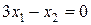 
.
Задача 4
а) Составить уравнение плоскости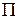 
, которая проходит через точку 
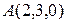и имеет нормальный вектор 
.
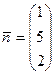б) Принадлежит ли этой плоскости точка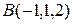 
?
Задача 5
Cоставить уравнение плоскости 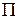, проходящей через три точки 
, 
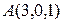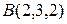и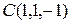 
.
Задача 6
Составить уравнение плоскости 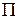, проходящей через точку 
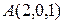и прямую 
.
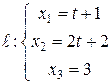Задача 7
Составить уравнение плоскости 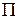, проходящей через две параллельные прямые 
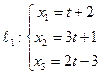и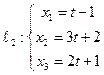 
.
Задача 8
Составить уравнение плоскости 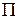, проходящей через точк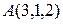и 
и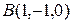 
параллельно вектору 
.
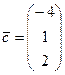Задача 9
Составить уравнение плоскости 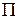, проходящей через две точк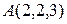и 
и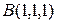 
перпендикулярно плоскости 
.
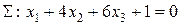Задача 10
Составить уравнение плоскости 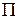, проходящей через точку 
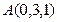параллельно плоскости 
.
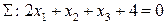Задача 11
При каком значении параметра a плоскост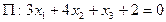и 
и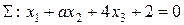 
будут перпендикулярны?
Задача 12
При каких значениях параметров a и b плоскост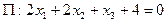и 
и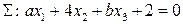 
будут параллельны?
Задача 13
Найти точку пересечения прямой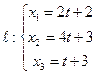 
и плоскости 
.
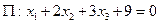Задача 14
Найти угол между прямой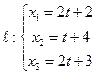 
и плоскостью 
.
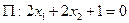Задача 15
Найти проекцию точки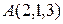 
на плоскость 
.
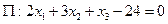Задача 16
Найти проекцию точки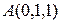 
на прямую 
.
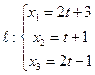Задача 17
Дана прямая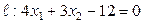 
. Найти угловой коэффициент этой прямой и отрезок, отсекаемый ею на оси ординат. Построить эту прямую.
Задача 18
Дана прямая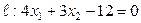 
и точка 
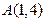. Составить уравнение:
а) прямой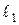 
,проходящей через точку A параллельно прямой ;
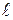б) прямой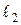 
, проходящей через точку A перпендикулярно прямой .
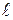Задача 19
Даны вершины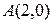 
, 
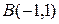и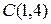 
треугольника ABC. Составить:
а) уравнение стороны BC;
б) уравнение высоты AH;
в) уравнение медианы AD.
Задача 20
Найти точку, симметричную точке А(1,2) относительно прямой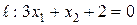 
.
Задача 21
Найти координаты какой-либо точки, принадлежащей данной кривой:
.
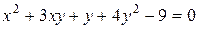Задача 22.Определить тип кривой и построить ее: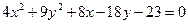 
.
Задача 23.Найти область, ограниченную линиям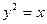и: 
и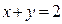 
.
Задача 24.Найти полярное уравнение и построить кривую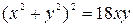 
.
Задача 25.Лежит ли точка А(-1,1,2) на поверхности, полученной вращением параболы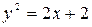 
вокруг оси Ох? Если нет, найдите, по крайней мере одну точку на этой поверхности.
Задача 26.Опишите область, которая получается в сечении фигуры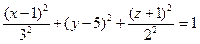 
плоскостью хОу.
Задача 27.Найдите точки пересечения прямой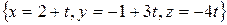 
с гиперболическим параболоидом 
.
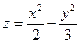II. Контрольные вопросы для самопроверки
1. Какой вид имеет уравнение плоскости в пространстве?
2. Как записать уравнение прямой в R3, проходящее через две заданные точки?
3. Как найти уравнение плоскости, проходящее через три заданные точки?
4. Как определить угол между прямой и плоскостью?
5. Каково условие параллельности прямой и плоскости?
6. Как найти угол между двумя прямыми в R2?
7. Как записывается условие ортогональности двух прямых в R2 с помощью угловых коэффициентов?
8. Какой вид имеет каноническое уравнение эллипса?
9. Что такое эксцентриситет эллипса?
10. Какой вид имеет каноническое уравнение гиперболы?
11. Как найти асимптоты гиперболы, зная ее каноническое управление?
12. Какое геометрическое место точек плоскости называется параболой?
13. Что такое фокусы эллипса?
14. Что представляет собой полярная система координат?
15. Написать канонические уравнения поверхностей второго порядка: эллиптического цилиндра, гиперболического цилиндра, сферы, эллипсоида вращения, однополостного и двуполостного гиперболоидов.