Контрольной работы по теме

«Ряды Фурье»

Задача 1. Разложить в ряд Фурье функцию 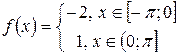, имеющую период .

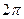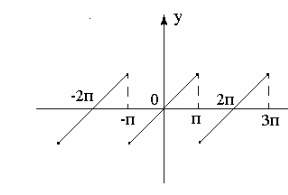
Решение. Построим график функции

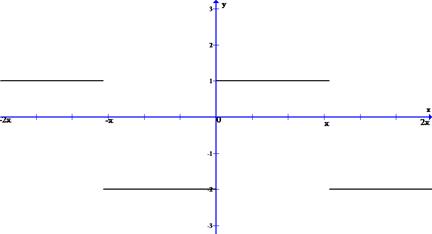
Эта функция f(x) имеет период 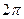, одну точку разрыва первого рода x=0 на отрезке 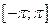, отрезок 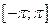можно разбить на два отрезка так, что внутри каждого из них функция f(x) монотонна.

По формуле (2) найдем коэффициент 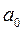этого ряда.

.

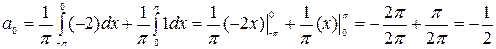Найдем 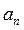по формуле (3)

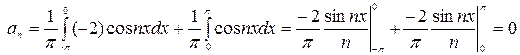
По формуле (4) 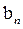найдем аналогичным образом

.

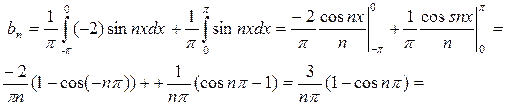
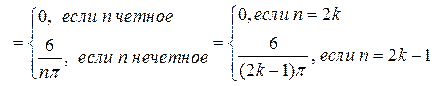Подставляя коэффициенты в формулу (1), получаем 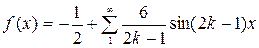или .

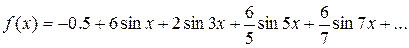Это равенство справедливо во всех точках, кроме точек разрыва. В каждой точке разрыва сумма ряда равна среднему арифметическому ее предельных значений изнутри отрезка, то есть в точке x=0.

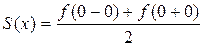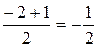= , а на концах отрезка в точках 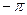и = .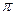

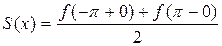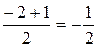
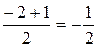Ответ.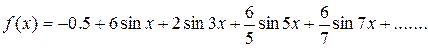

Построим график S₄(x)

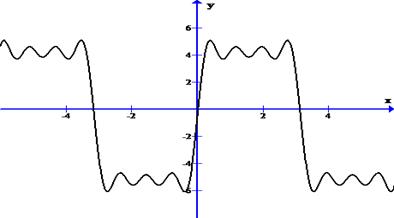
Задача 2. Разложить в ряд Фурье функцию 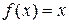, заданную на отрезке 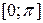сначала по синусам, затем по косинусам.

Решение.Построим график

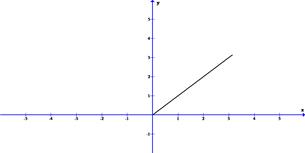
1. Продолжая эту функцию на промежуток 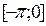нечетным образом, получим функцию, ряд Фурье для которой составлен в §2, пример 2.

Ряд для такого разложения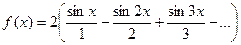

Построим S₅(x)

2. Продолжая эту функцию на промежуток 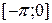четным образом. Построим график

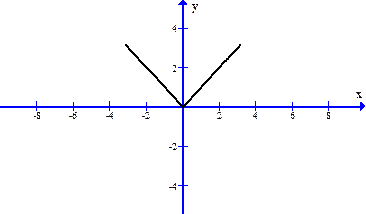
Эта функция f(x) имеет период 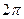, четная, продолжена непрерывно.

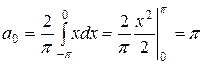. Найдем =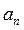

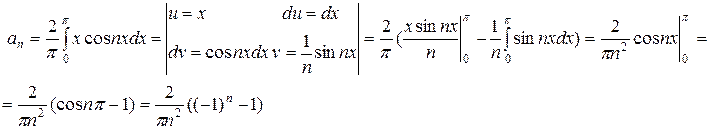
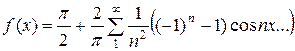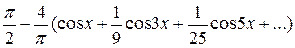
Это равенство справедливо во всех точках числовой прямой.

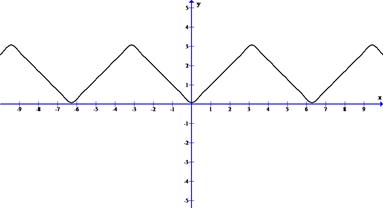
Построим график S₄(x)

Задача3.Разложить в ряд Фурье периодическую функцию 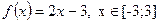, с периодом Т=6.

Решение. Построим эскиз графика функции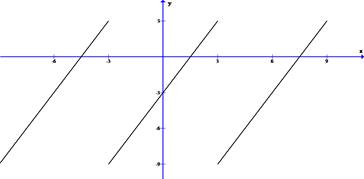

Проверив выполнение условий Дирихле для функции, переходим к вычислению коэффициентов Фурье. Заданная функция общего вида с периодом Т=6, l=3, поэтому в разложении ее ряд Фурье имеет вид: .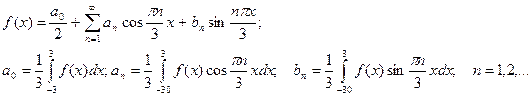

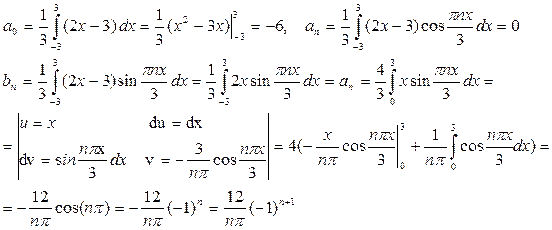
Подставляя коэффициенты в формулу ряда, получаем 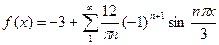или 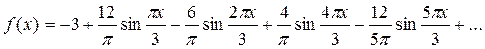. Это равенство имеет место во всех точках, кроме точек -3 и 3. В каждой из этих точек сумма ряда равна среднему арифметическому ее предельных значений справа и слева, то есть .

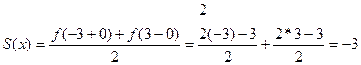Построим график S₅ (x)

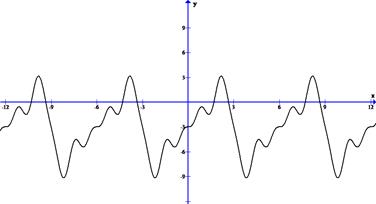
Можно совместить оба графика на одном чертеже

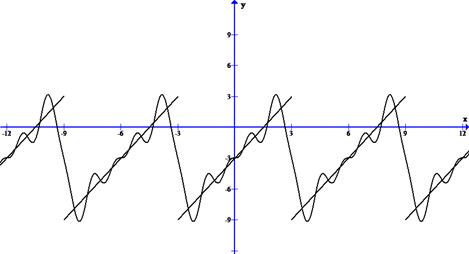
Отметим близость этих графиков.

Задача4. Разложить в ряд Фурье функцию 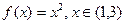. Построить график S₅(x).

Решение. Будем считать функцию периодической с периодом T=3-1=2, l=1 т.е. 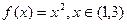, T=2, l=1. Построим эскиз графика этой функции

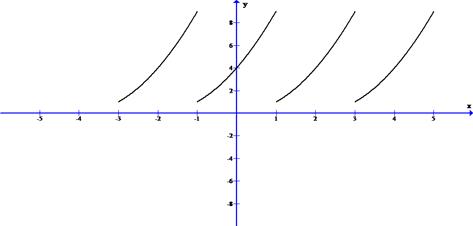
Ряд Фурье для этой функции будет иметь следующий вид: .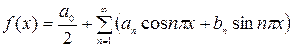

Проверив выполнение условий Дирихле для функции, переходим к вычислению коэффициентов Фурье. .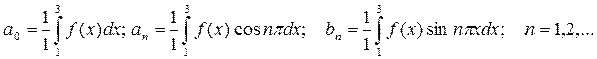

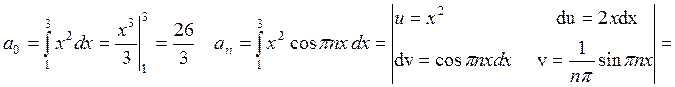
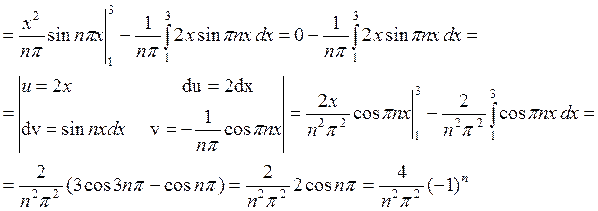
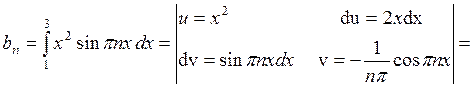
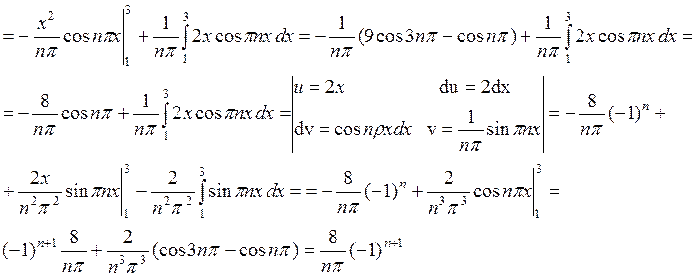Подставляя коэффициенты в формулу ряда, получаем 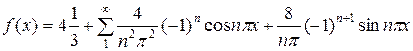или 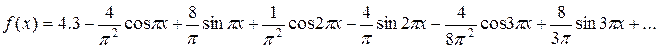Это равенство имеет место во всех точках, кроме точек 1 и 3. В каждой из этих точек сумма ряда равна среднему арифметическому ее предельных значений справа и слева, то есть .

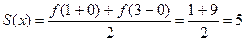Построим график S₅ (x)

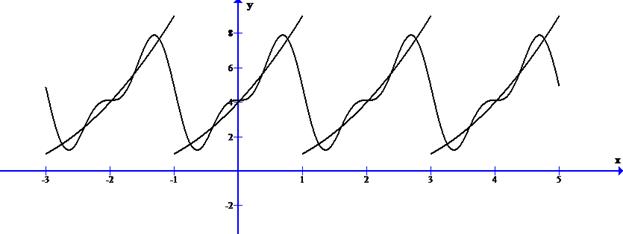
Задача 5. Разложить в комплексный ряд Фурье периодическую функцию с периодом 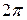, определенную следующим образом: 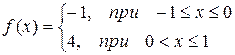. Построить амплитудно-частотный спектр.

Решение. Будем считать функцию периодической с периодом Т =2. Построим график.

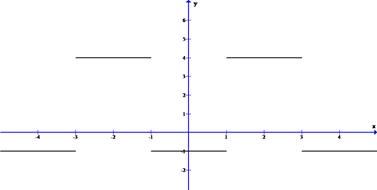
Проверив выполнение условий Дирихле для функции 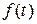, переходим к вычислению коэффи­циентов Фурье по формуле .

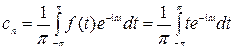Интеграл, стоящий в правой части последнего равенства, опре­деляется по частям:

;

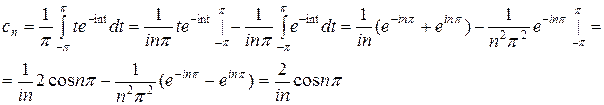
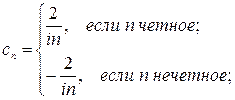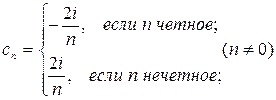
Если 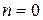, то полученные формулы не дают результата. Поэтому коэффициент 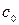надо вычислить иначе׃ 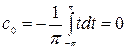, так как интеграл от нечетной функции по симметричному промежутку равен нулю. Окончательно получим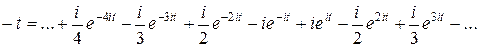

Это равенство имеет место лишь в точках непрерывности функции 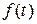. В точках разрыва 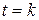, где k- любое нечетное число, сумма ряда равна нулю. Построим амплитудно-частотный спектр

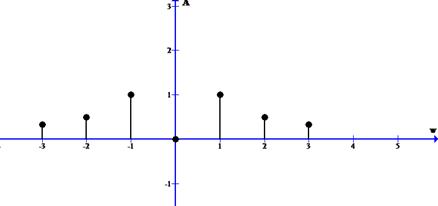
Задача 6. Разложить в ряд Фурье по косинусам функцию f(x), графически заданную на промежутке [0; 2] (получить первые 4 гармоники разложения).

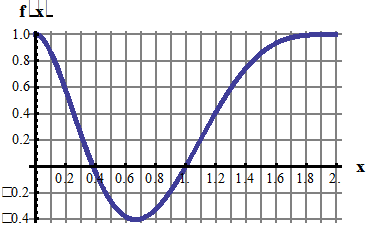
Решение. По условию функция – четная, задана на отрезке [0; 2] = [0; l], следовательно, ее график на промежутке [–2; 0] симметричен заданному графику относительно оси ординат и период функции T = 2l =4 (длина промежутка [–2; 2]).

Ряд Фурье для четной периодической функции 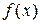с периодом 2l имеет вид:

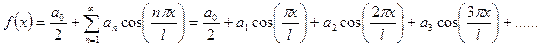, (1)

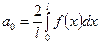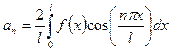где , . (2)

Поскольку вид функции 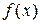) неизвестен, для вычисления интегралов используем одну из квадратурных формул – формулу средних прямоугольников:

,

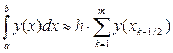где 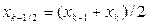– середина k-го отрезка разбиения промежутка интегрирования [a; b], k = 1, 2, …, m, h – длина шага разбиения промежутка интегрирования: .

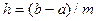Возьмем m = 10, 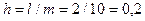, т.е. разобъем отрезок [0; 2] на 10 равных частей точками 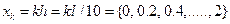и считаем с графика значения функции в серединах полученных отрезков. Чтобы вычислить коэффициенты a₀, a₁, a₂, a₄ для первых 4 гармоник разложения функции в ряд Фурье по формулам (2), построим таблицу значений функции f(x) и 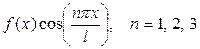в полученных точках:

k	xk-1/2	f(xk-1/2)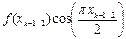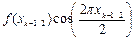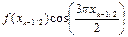
	0,1	0,9	0,89	0,86	0,80
	0,3	0,25	0,22	0,15	0,04
	0,5	– 0,25	– 0,18		0,18
	0,7	– 0,4	– 0,18	0,24	0,40
	0,9	– 0,2	– 0,03	0,19	0,09
	1,1	0,2	– 0,03	– 0,19	0,09
	1,3	0,6	– 0,27	– 0,35	0,59
	1,5	0,85	– 0,60		0,60
	1,7	0,9	– 0,80	0,53	– 0,14
	1,9		– 0,99	0,95	– 0,89
	3,85	– 1,97	2,38	1,76

Вычислим коэффициенты ряда a₀, a₁, a₂, a₄.

;

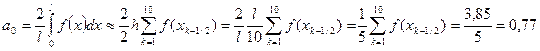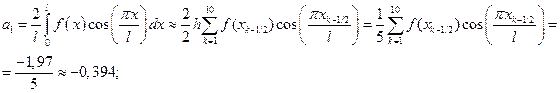
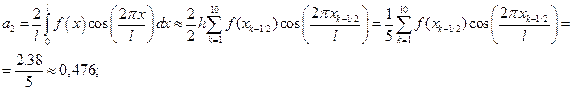
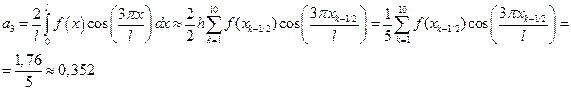
Подставляем найденные коэффициенты в формулу (1) и получаем аппроксимацию функции частичной суммой ряда s₃(x):

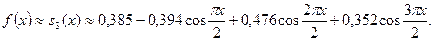
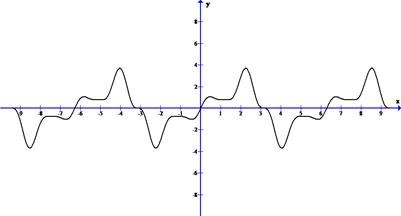
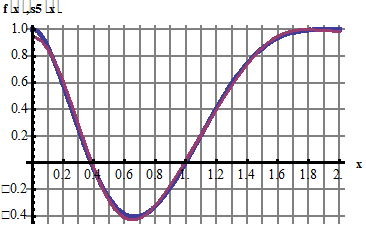
Для сравнения с функцией f(x) построим на промежутке [0; 2] график заданной функции f(x) и график полученной аппроксимации :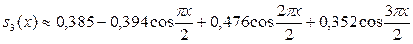

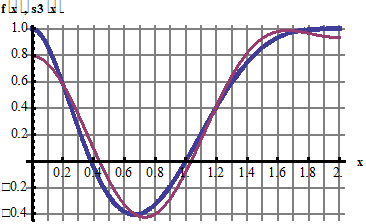
Если в аппроксимацию s_n(x) включить сумму большего числа гармоник, например, 5, то графики s₅(x) и функции f(x) практически совпадают:

Ответ: , .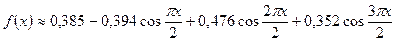

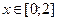Варианты контрольной работы по теме «Ряды Фурье»

Задача 1.

Построить эскиз графика, разложить в ряд Фурье следующие функции, периодические с периодом 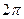, определить сумму в точках разрыва. Построить график частичной суммы Фурье для n=4.

№	Функция	№	Функция

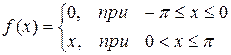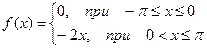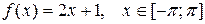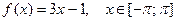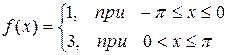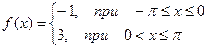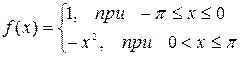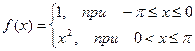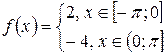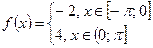Задача 2. Разложить в ряд Фурье функцию 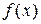, заданную формулой на отрезке 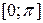, сначала по синусам, затем по косинусам. Построить график 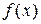и частичных сумм для n=4.

№	Функция	№	Функция
	f(x)=2x-1		f(x)=x-4
	f(x)=x2-1		f(x)=x2+2
	f(x)=-x-1		f(x)=-x-3
	f(x)=x2+1		f(x)=x2-3
	f(x)=3x-2		f(x)=0.5x-1

Задача3.Разложить в ряд Фурье периодическую функцию 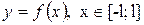, с периодом Т=2l. Построить график частичной суммы при n=5.

№	Функция	T	№	Функция	T
	f(x)=x+4			f(x)=2x+1
	f(x)=-x+4			f(x)=2x-1
	f(x)=2x+4			f(x)=3x+4
	f(x)=x+1			f(x)=3x-2
	f(x)=-x+2			f(x)=-3x-1

Задача4Разложить в ряд Фурье функцию 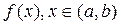. Построить график частичной суммы S₄(x).

№	Функция	№	Функция

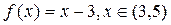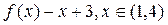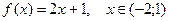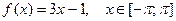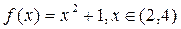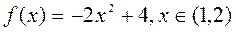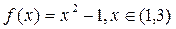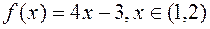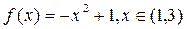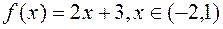Задача 5. Разложить в комплексный ряд Фурье периодическую функцию с периодом 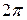, определенную следующим образом: 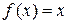, 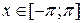. Построить амплитудно-частотный спектр.

№	Функция	№	Функция

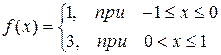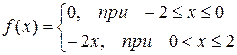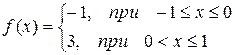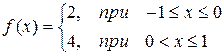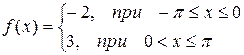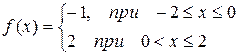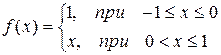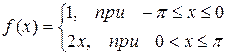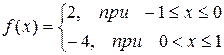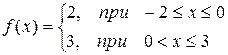Задача 6. Разложить в ряд Фурье функцию f(x), графически заданную на промежутке [0; l] (получить первые гармоники разложения).

Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; π] (получить первые 4 гармоники разложения).

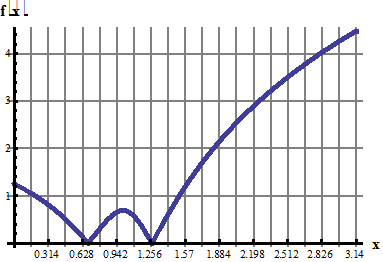
1. Разложить в ряд Фурье по косинусам функцию f(x), графически заданную на промежутке [0; 1] (получить первые 4 гармоники разложения).

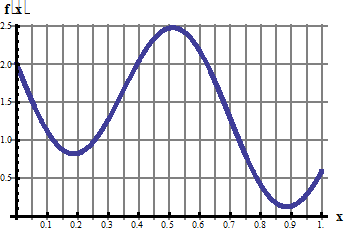
2. Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; 2] (получить первые 4 гармоники разложения).

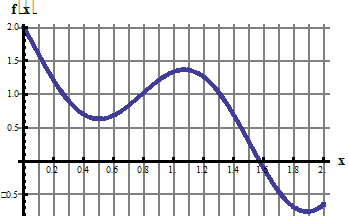
3. Разложить в ряд Фурье по косинусам функцию f(x), графически заданную на промежутке [0; 2,5] (получить первые 4 гармоники разложения).

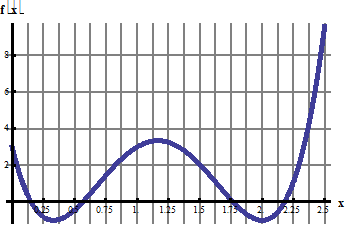
4. Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; 3] (получить первые 4 гармоники разложения).

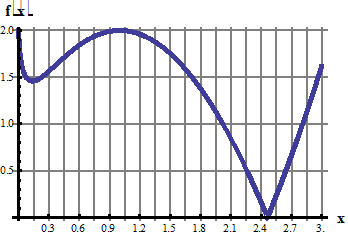
5. Разложить в ряд Фурье по косинусам функцию f(x), графически заданную на промежутке [0; π] (получить первые 4 гармоники разложения).

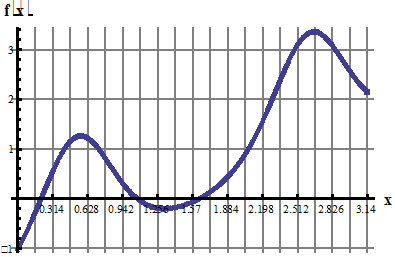
6. Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; 4] (получить первые 4 гармоники разложения).

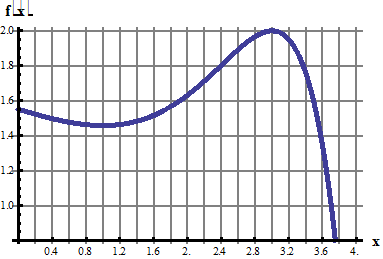
7. Разложить в ряд Фурье по косинусам функцию f(x), графически заданную на промежутке [0; 5] (получить первые 4 гармоники разложения).

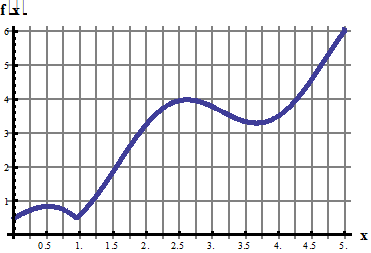
8. Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; π] (получить первые 4 гармоники разложения).

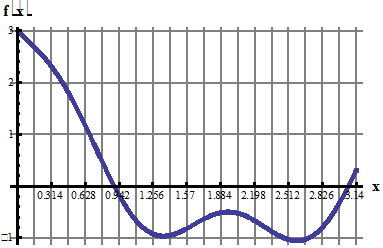
9. Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; 1] (получить первые 4 гармоники разложения).

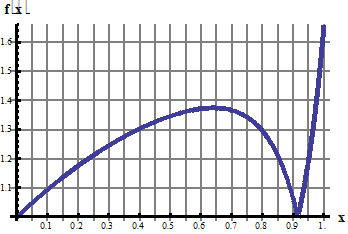
Рекомендуемая литература

1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. –М.: Айрис-пресс, 2003. – 288 с.

2. Щипачев, В.С. Высшая математика: учебник для вузов / В.С. Щипачев.– М.: Высш. шк., 1998.– 479 с.

3.Берман Г.Н. Сборник задач по курсу математического анализа: Уч. пособие.- 22-изд., перераб.- СПб., Изд-во «Профессия», 2005.-432с.

4. Щипачев, В.С. Задачник по высшей математике / В.С. Щипачев.– М.: Высш. шк., 2001.– 304 с.