Метод непосредственного интегрирования

Интегрирование, основанное на прямом использовании таблицы интегралов и свойств неопределенного интеграла, называется непосредственным интегрированием.

При непосредственном интегрировании могут представиться три случая.

I. Интеграл находят непосредственно по соответствующему табличному интегралу.

Примеры

1) ;

2) ;

II. Интеграл приводится к одному или нескольким табличным интегралам в результате применения свойств неопределенного интеграла.

Примеры

1.

;

2.

.

III. Интеграл приводится к одному или нескольким табличным интегралам в результате элементарных тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла.

Примеры

1.

;

2. ;

;

4.

.

Метод интегрирования подстановкой (замена переменной)

Сущность метода заключается в том, что путем введения новой переменной интегрирования (т.е. подстановки) удается свести заданный интеграл к новому интегралу, который является табличным или легко находится другим способом. Общих методов подбора подстановок не существует. Рассмотрим некоторые варианты подстановок.

Линейные подстановки

При сведении данного интеграла к табличному часто используются преобразования дифференциала (операция «подведения под знак дифференциала»).

I. Под знак дифференциала, стоящего в интеграле, можно ввести любое постоянное слагаемое.

При любой постоянной а будет

.

Поэтому

.

Примеры

1. ;

2. ;

3. .

II. Под знак дифференциала, стоящего в интеграле, можно ввести любой постоянный множитель, разделив на него интеграл.

Известно, если а − постоянно, то

.

Тогда

.

Поэтому

.

Примеры

1. ;

2. ;

3. .

В некоторых случаях применяют оба приема вместе:

,

где а и b − постоянные.

Примеры

2. ;

3. .

Подстановка вида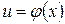

Если под знаком интеграла стоит сложная функция, умноженная на производную от внутренней функции, т.е. интеграл имеет вид:

,

то этот интеграл можно упростить, если заменить внутреннюю функцию новой переменной .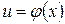

Тогда получим

.

В данном случае была применена операция «подведения под знак дифференциала» ( ).

Для применения подстановки 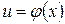существует следующее правило.

Правило.

Чтобы найти интеграл , надо

1) переписать интеграл в виде

;

2) сделать замену 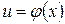, что приведет к интегралу

;

3) найти последний интеграл;

4) в полученном ответе произвести обратную замену u на .

Примеры

1.

;

2. ;

3. ;

4. .

Подстановка вида

Пусть требуется найти интеграл

.

Иногда бывает целесообразно при вычислении такого интеграла, в котором независимой переменой является х, сделать подстановку . Преобразуя подынтегральное выражение путем подстановки, имеем

,

так как .

В результате получаем формулу интегрирования подстановкой :

.

Замечание.

Функция выбирается так, чтобы интеграл в правой части равенства был более простым, чем первоначальный.

Сформулируем правило подстановки.

Правило.

Чтобы найти интеграл , надо

1) перейти к новой переменной t, связанной с х выражением ;

2) выразить через t все подынтегральное выражение :

;

3) найти новый интеграл:

;

4) в полученном ответе произвести обратную замену на х.

Примеры

1.

2.

.