Теорема 3 о логическом следствии
Формула алгебры логики 
является логическим следствием формулы алгебры логики 
,тогда и только тогда, если
.
Доказательство.
Пусть n - количество различных переменных, входящих в формулы 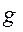и ,и а n - мерный двоичный набор из 0 и 1.
Пусть 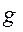,покажем что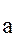
.
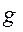
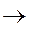
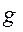
Так какявляется следствием из 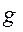,то на любом наборе а, если 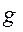(а)=1, то (а)=1. Если же 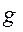(а)=0, то 0 принимает значение 1 при любом значении(а).
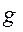
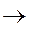
Пусть ,покажем, что .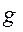
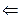
-следствие из 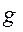,если при любом наборе а,из 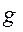(а)=1 следует(а)=1.
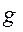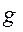
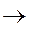
Пусть а,такой набор, что (а)=1, тогда из того, что -тождественно истинная формула, её значение на наборе а должно равняться 1, а это для операции импликации может быть лишь тогда, когда (а)=1.
Теорема доказана.
Аналогичным образом доказывается и более общая теорема.
Обобщенная теорема 4 о логическом следствии.
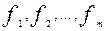
тогда и только тогда, если 
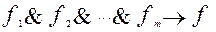
Следствие из теоремы 4.
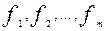
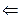
тогда и только тогда, если при любом p,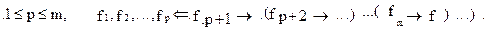 
ри доказательстве следствия кроме теоремы 4 используется и определение операции импликации.
Определение.
Множество формул алгебры логики { 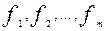} называется непротиворечивым,если существует по крайней мере один такой набор значений переменных, входящих в эти формулы, что все формулы из множества на этом наборе равны 1.
Множество формул алгебры логики { 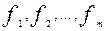} называется противоречивым,если при всяком наборе значений переменных, входящих в эти формулы , по крайней мере одна из формул принимает значение 0.
Отсюда, {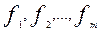 
} -непротиворечиво, если 
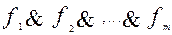=1по крайней мере на одном наборе и противоречиво, если 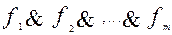=0для любого набора значений переменных.
Теорема 5 о противоречивости множества формул алгебры логики.
Множество формул алгебры логики противоречиво, если из него в качестве логического следствия можно вывести противоречие.
Для доказательства теоремы используется теорема 1 и определение операции импликации.
Теорема 6 о тождественной истинности формулы алгебры логики.
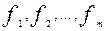
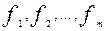,если в качестве логического следствия из и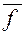 
можно вывести противоречие.
Основные схемы доказательств: если x то y, доказательство от противного, доказательство построением цепочки импликаций, доказательство разбором случаев.
На основании выше доказанных теорем рассмотрим следующие схемы доказательств.
Схема 1.
Доказательство теорем типа “если x, то y”.
Схема доказательства основана на следующем логическом следствии:
.
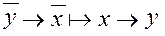Действительно, по теореме 3 из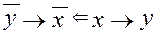 
следует
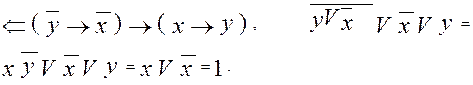
Схема 2.
Доказательство от противногоили метод косвенного доказательства.
Схема доказательства основана на следующем логическом следствии:
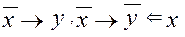
Действительно, по теореме 4 из 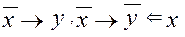следует, что
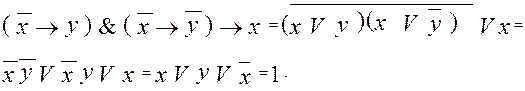
Схема 3.
Доказательство построением цепочки импликаций.
Схема доказательства основана на следующем логическом следствии:
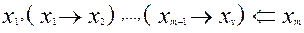
Действительно, по теореме 4 из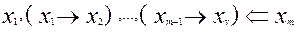 
следует, что
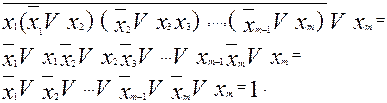
Схема 4.
Доказательство разбором случаев.
Схема доказательства основана на следующем логическом следствии:
.
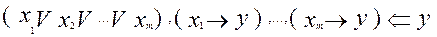Действительно, по теореме 4 из 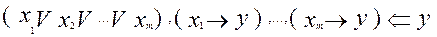следует, что
