III. Предел функции в точке и непрерывность

Ф 20-014

Утверждено

Протокол заседания кафедры

№ 11 от 11. 11.15

Экзаменационная программа по высшей математике для студентов специальности экономика и управление на предприятии (зимняя сессия)

I. Аналитическая геометрия

Обязательный начальный уровень: Формула расстояния между двумя точками на прямой и на плоскости, формула деления отрезка в данном соотношении, различные типы уравнения прямой, уметь получать уравнения прямой и строить прямую. Взаимное расположение двух прямых на плоскости, условия параллельности и перпендикулярности прямых. Канонические уравнения окружности, эллипса, параболы и гиперболы, формулы связи между их параметрами.

1. Простейшие задачи аналитической геометрии на плоскости.

2. Различные виды уравнения прямой на плоскости (с выводами формул).

3. Угол между двумя прямыми. Исследование взаимного расположения двух прямых на плоскости, заданных общим уравнением.

4. Эллипс, его свойства и параметры. Доказательство теоремы о необходимом и достаточном условии того, что точка лежит на эллипсе.

5. Гипербола, её свойства и параметры. Доказательство теоремы о необходимом и достаточном условии того, что точка лежит на гиперболе.

6. Парабола, её свойства и параметры. Доказательство теоремы о необходимом и достаточном условии того, что точка лежит на параболе. Различные способы расположения параболы относительно координатных осей.

II.Предел числовой последовательности

Обязательный начальный уровень: определение числовой последовательности, ограниченной последовательности, 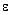-окрестности точки а, бесконечно малой последовательности (БМП), бесконечно большой последовательности (ББП), определение предела числовой последовательности. Примеры для каждого типа последовательностей.

7. Числовая последовательность. Ограниченные и неограниченные последовательности и их геометрическое толкование. Примеры. Монотонные последовательности. Примеры.

8. Предел числовой последовательности и его геометрический смысл. Свойства сходящихся последовательностей. Примеры.

9. БМП. Свойства БМП. Теорема о сумме двух БМП (доказательство).

10. ББП. Свойства ББП. Теорема о связи БМП и ББП (доказательство).

III. Предел функции в точке и непрерывность

Обязательный начальный уровень: понятие функции, обратной функции, сложной функции, предел функции в точке (на языке последовательностей и на языке " 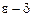"), бесконечно малая функция (БМФ) при 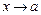и бесконечно большая функция (ББФ) при 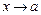и примеры, два замечательных предела и их следствия, определение непрерывности функции в точке, определение точки разрыва функции, классификация точек разрыва, графики основных элементарных функций (знать область определения и множество значений).

1. Понятие функции. Способы задания функции. График функции. Ограниченные функции Чётные, нечётные, периодические и монотонные функции. Примеры.
2. Понятие обратной функции. Примеры. Понятие сложной функции. Примеры. Классификация функций.
3. Графики основных элементарных функций: линейной, степенной, показательной, логарифмической, тригонометрических, обратных тригонометрических. Знать их области определения и множество значений.
4. Определение предела функции при 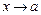по Гейне. Исследование существование предела .
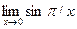5. Определение предела функции по Коши. Определение предела на языке окрестностей. Геометрический смысл предела функции в точке.
6. Определение односторонних пределов функции в точке на языке последовательностей и на языке 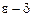. Теорема о связи предела функции в точке с односторонними пределами.
7. БМФ при 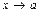. Свойства БМФ при 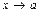. Теорема о сумме двух БМФ при 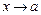(доказательство).
8. БМФ при 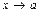. Свойства БМФ при 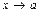. Теорема о произведении БМФ при 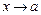на ограниченную функцию (доказательство).
9. Свойства предела функции. Теоремы о единственности предела функции и о связи с пределом БМФ. Алгебраические свойства предела функции.
10. ББФ при 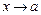. Свойства ББФ при 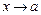. Теорема о связи понятий БМФ и ББФ при 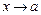(доказательство).
11. Теорема о пределе промежуточной функции (доказательство).
12. Первый замечательный предел (доказательство). Второй замечательный предел. Следствия.
13. Определение непрерывности функции в точке х=а. Определения на языке последовательностей, на языке 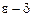, на языке приращений. Алгебраические свойства непрерывных в точке функций.
14. Определение односторонней непрерывности в точке. Связь непрерывности функции в точке с односторонней непрерывностью.
15. Точки разрыва. Их классификация. Примеры.
16. Непрерывность сложной функции. Непрерывность обратной функции.
17. Теоремы о непрерывных на отрезке функциях (5 теорем) и их геометрическая интерпретация.

IV. Производная.

Обязательный начальный уровень: определение производной, её геометрический и физический смысл, уравнение касательной, правила дифференцирования, таблица производных. Дифференциал (определение и формула для вычисления).

1. Определение производной функции в точке. Примеры вычисления производной по определению. Физический и геометрический смысл производной. Уравнение касательной и нормали.
2. Теорема о связи существования производной и непрерывности функции в точке. Иллюстрация того, что функция 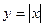не имеет производной в точке x=0.
3. Правила дифференцирования (с выводом формул).
4. Таблица производных (с выводом формул).
5. Теорема о производной обратной функции и производной сложной функции.
6. Дифференцируемость функции в точке. Теорема о необходимом и достаточном условии дифференцируемости функции в точке (доказательство).
7. Дифференциал функции. Применение в приближённых вычислениях.
8. Основные теоремы дифференциального исчисления и их геометрическая интерпретация.
9. Правило Лопиталя (доказательство). Раскрытие неопределённостей: 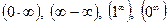и т.д. по правилу Лопиталя.