С постоянными коэффициентами
Не существует общих методов для нахождения в конечном виде общего решения линейного уравнения с переменными коэффициентами. Однако для ДУ с постоянными коэффициентами такой метод существует.
Определение 2.5.ЛОДУ второго порядка с постоянными коэффициентами называется ДУ вида
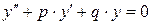, (2.3)
где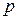 
и 
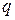- постоянные действительные числа.
Для нахождения общего решения ЛОДУ второго порядка с постоянными коэффициентами достаточно найти два линейно независимых частных решения.
Будем искать частные решения в ви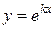де 
, где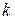 
- некоторое число (предложено Л.Эйлером). Тогда
, 
.
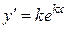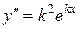Подставляем полученные выражения производных в уравнение (2.3), получаем:
.
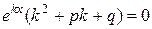Так как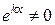 
, то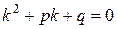 
.
Следовательно, если 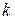будет удовлетворять полученному приведенному квадратному уравнению, то 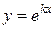будет решением уравнения (2.3).
Уравнение 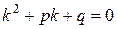называется характеристическим уравнением по отношению к уравнению (2.3).
Поскольку характеристическое уравнение является квадратным уравнением, то возможны следующие случаи по наличию корней:
1. 
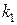и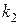 
- два различных действительных корня;
2. 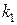и 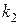- два равных действительных корня;
3. 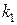и 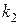- два комплексных корня;
Рассмотрим каждый случай отдельно.
I. Корни характеристического уравнения действительны и различны: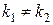 
.
В этом случае частными решениями будут функци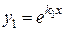и 
и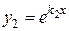 
. Эти решения линейно независимы. Следовательно, общее решение имеет вид
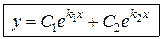. (2.4)
II. Корни характеристического уравнения действительны и равны: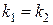 
.
В этом случае частными решениями будут функци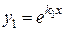и и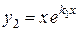 
(можно убедиться, подставив функцию 
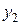в исходное ДУ). Эти решения линейно независимы. Следовательно, общее решение имеет вид
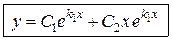. (2.5)
III. Корни характеристического уравнения комплексные числа: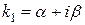 
и 
.
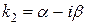Общее решение имеет вид
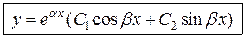. (2.6)
Пример 2.3. Решить ЛОДУ второго порядка: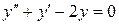 
.
Решение. Составляем и решаем характеристическое уравнение:
.
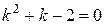Находим корни характеристического уравнения: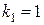 
и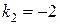 
.
Общее решение примет вид
.
,
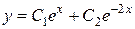Пример 2.4. Решить ЛОДУ второго порядка: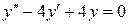 
.
Решение. Составляем и решаем характеристическое уравнение:
.
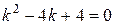Находим корни характеристического уравнения: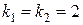 
.
Общее решение примет вид
.
,
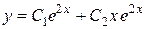Пример 2.5. Решить задачу Коши для ЛОДУ второго порядка:
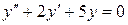
при начальных условиях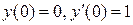 
Решение. Составляем и решаем характеристическое уравнение:
.
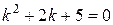Находим корни характеристического уравнения: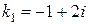 
и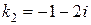 
.
Общее решение примет вид
.
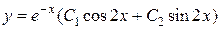Найдем частное решение, удовлетворяющее данным начальным условиям. Определим соответствующие значения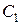 
и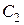 
. Сначала найдем 
:
.
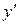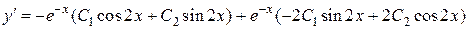Далее получаем
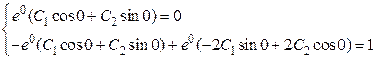Þ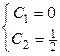 
.
Таким образом, частное решение: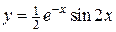 
.
,
Пример 2.6. Решить ЛОДУ второго порядка: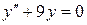 
.
Решение. Составляем и решаем характеристическое уравнение:
.
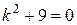Находим корни характеристического уравнения: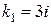 
и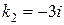 
.
Общее решение примет вид
.
,
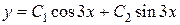