Предел и непрерывность функции

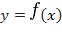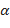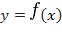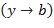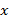Определение 4.5. Пусть функция определена в некоторой окрестности точки или в некоторых точках этой окрестности. Функция стремится к пределу в при , стремящемся к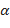 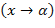, если для каждого положительного числа 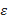, как бы мало оно ни было, можно указать такое положительное число 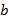, что для всех 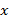, отличных от 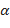и удовлетворяющих неравенству 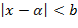имеет место неравенство 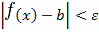. Если 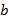есть предел функци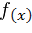и при 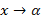, то пишут: .

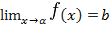Определение 4.6. Функция 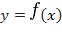называется непрерывной при значении 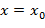( или в точке 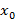), если она определена в некоторой окрестности точки 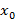и если

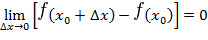
Определение 4.7. Если функция 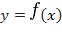непрерывна в каждой точке некоторого интервала 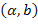, где 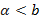, то говорят, что функция непрерывна на этом интервале.

Свойства пределов.

Теорема 1:Предел алгебраической суммы двух, трёх и вообще определённого числа переменных равен алгебраической сумме пределов этих переменных:

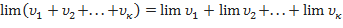
Пример №3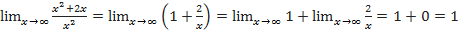

Теорема 2: Предел произведения двух, трёх или вообще определённого числа переменных равен произведению пределов этих переменных

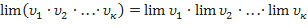
Пример №4 .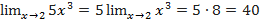

Теорема 3: Предел частного двух переменных равен частному пределов этих переменных, если предел знаменателя отличен от нуля: .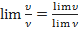

Пример №5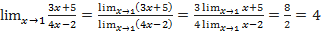

Пример №6Найти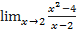

Здесь знаменатель и числитель при 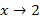стремится к нулю, и, следовательно, теорема 3 неприменима. Произведём следующее тождественное преобразование:

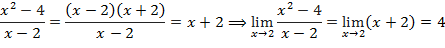
Первый замечательный предел:

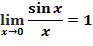
Второй замечательный предел:

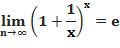
Задания: Вычислить указанные пределы:

1) ;

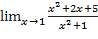2) ;

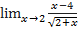3) ;

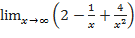4) ;

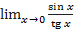5) ;

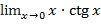6) ;

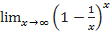7) ;

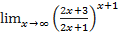8) ;

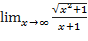9) .

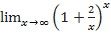Производная и дифференциал функции одной переменной.

Определение 4.8.Производной функции 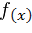в точке 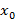называется предел отношения приращения 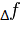функции в этой точке к приращению 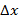аргумента, когда последнее стремится к нулю: .

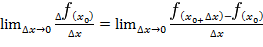Функция 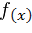, имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке.

Для производной функции 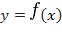употребляются следующие обозначения: 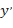, , 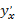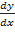или 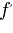, , 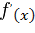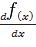. Нахождение производной называется дифференцированием.

Пример №7 Дана функция 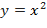, найти её производную :

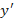a) В произвольной точке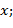

b) при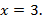

Решение:

a) При значении аргумента, равном 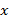, имеем 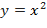. При значении аргумента, равном 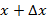, имеем: .

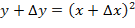Находим приращение функции: 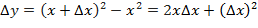. Составляем отношение 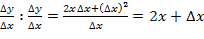. Переходя к пределу, найдём производную от данной функции: .

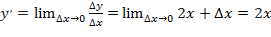Итак, производная от функции 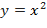в произвольной точке равна .

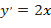b) При 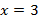получим: .

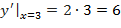Основные правила дифференцирования. Производные степени и корня.

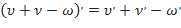1. ( 1 )
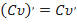2. ( 2 )
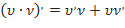3. ( 3 )
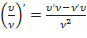4. ( 4 )

Частные случаи формулы (4): ;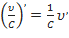

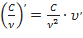
При вычислении производных необходимо помнить, что 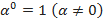; ; 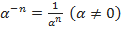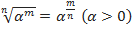, и знать следующие правила действий со степенями и корнями:
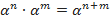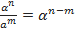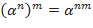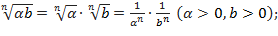
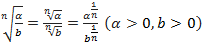; ; ; , здесь 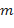и 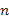- любые рациональные числа.