III. Предел функции в точке и непрерывность

Ф 20-014

Вопросы и задания к экзаменам и зачетам

Утверждено

Протокол заседания кафедры

Вопросы к экзамену по дисциплине Высшая математика

1 курс, экономические специальности ФЭУ дневной формы обучения

I. Аналитическая геометрия

Обязательный начальный уровень: основные формулы аналитической геометрии, различные типы уравнения прямой, условия параллельности и перпендикулярности прямых. Канонические уравнения окружности, эллипса, параболы и гиперболы, формулы связи между их параметрами.

1. Простейшие задачи аналитической геометрии на плоскости (c выводами формул).
2. Различные виды уравнения прямой на плоскости (с выводами формул). Доказательство теоремы об общем уравнении прямой.
3. Угол между двумя прямыми. Исследование взаимного расположения двух прямых на плоскости, заданных общим уравнением.
4. Эллипс, его свойства и параметры. Доказательство теоремы о необходимом и достаточном условии того, что точка лежит на эллипсе.
5. Гипербола, её свойства и параметры. Доказательство теоремы о необходимом и достаточном условии того, что точка лежит на гиперболе.
6. Парабола, её свойства и параметры. Доказательство теоремы о необходимом и достаточном условии того, что точка лежит на параболе. Различные способы расположения параболы относительно координатных осей.

II.Предел числовой последовательности

Обязательный начальный уровень: определение числовой последовательности, ограниченной последовательности, 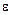- окрестности точки а , бесконечно малой последовательности (БМП), бесконечно большой последовательности (ББП), строго монотонной последовательности, определение предела числовой последовательности. Примеры для каждого типа последовательностей.

1. Числовая последовательность. Ограниченные и неограниченные последовательности. Примеры. Окрестность, 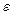- окрестность точки 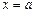. Геометрическое толкование ограниченной последовательности.
2. Предел числовой последовательности и его геометрический смысл. Свойства сходящихся последовательностей. Определение БМП и ББП. Примеры.
3. БМП. Свойства БМП. Доказательство теоремы о сумме двух БМП.
4. БМП. Свойства БМП. Доказательство теоремы о произведении БМП на ограниченную посл. БМП и ББП. Доказательство теорем (прямой и обратной) о связи БМП и ББП.

11. Предельный переход в неравенствах. Доказательство теоремы и следствия. Строго монотонные последовательности. Примеры. Теорема о монотонной ограниченной последовательности.

III. Предел функции в точке и непрерывность

Обязательный начальный уровень: понятие функции, обратной функции, сложной функции, предел функции в точке (на языке последовательностей и на языке " 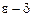"), бесконечно малая функция (БМФ) при 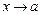и бесконечно большая функция (ББФ) при 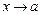и примеры, два замечательных предела и их следствия, определение непрерывности функции в точке, определение точки разрыва функции, классификация точек разрыва, графики основных элементарных функций (знать область определения и множество значений).

1. Понятие функции. Способы задания функции. График функции. Ограниченные функции. Примеры. Понятие обратной функции. Примеры. Понятие сложной функции. Примеры.
2. Графики основных элементарных функций: линейной, степенной, показательной, логарифмической, тригонометрических, обратных тригонометрических. Знать их области определения и множество значений.
3. Определение предела функции при 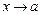по Гейне. Исследование существования предела 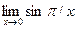. Определение предела функции по Коши. Определение предела на языке окрестностей. Геометрический смысл предела функции в точке.
4. Определение односторонних пределов функции в точке на языке последовательностей и на языке 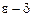. Связь предела функции в точке с односторонними пределами.
5. БМФ при 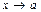. Определение и примеры. Свойства БМФ.
6. Доказательство теоремы о сумме двух БМФ при 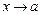. Доказательство теоремы о произведении БМФ на ограниченную, на константу или другую БМФ.
7. ББФ при 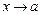. Определение и примеры. Доказательство теорем (прямой и обратной) о связи понятий БМФ и ББФ при 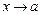. Свойства ББФ при .
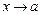8. Алгебраические свойства предела функции. Доказательство утверждений о сумме и произведении двух функций, имеющих предел в точке. Док-во принципа “2-х милиционеров”.
9. Первый замечательный предел с доказательством. Второй замечательный предел. Следствия.
10. Определение непрерывности функции в точке х=а. Переформулировка определения на языке последовательностей, на языке 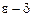, на языке приращений. Алгебраические свойства непрерывных в точке функций.
11. Определение односторонней непрерывности в точке.Связь непрерывности функции в точке с односторонней непрерывностью.
12. Точки разрыва. Их классификация. Примеры.
13. Непрерывность сложной функции. Непрерывность обратной функции. Теоремы о непрерывных на отрезке функциях (5 теорем). Где возможно, привести геометрическую иллюстрацию

IV. Производная.

Обязательный начальный уровень: определение производной, её геометрический и физический смысл, уравнение касательной, правила дифференцирования, таблица производных. Дифференциал (определение и формула для вычисления).