Теорема о непрерывности дифференцируемой ФНП в точке

Понятие градиента. Свойства градиента (3 свойства доказать)

Градие́нт (gradientis — шагающий, растущий) — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины 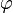, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный быстроте роста этой величины в этом направлении.

Пусть дана функция . U=f(x,y,z) определенная и дифференцируема в некоторой области Д.

Градиентом функции называется вектор проекции которого на оси координат равны соответствующим частным производным.

grad U=(∂U/∂х)i+(∂U/∂у)j+(∂U/∂z)k

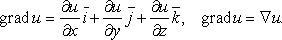
Линией уровня называется линия на которой функция принимает постоянное значение u(x,y)=с. Геометрический смысл градиента состоит в том что градиент указывает направление наибольшего изменения функции.

Свойства градиента:

1. Производная по направлению имеет МАХ значение в направлении совпадающем с градиентом.

2. Производная в направлении ⊥ градиенту равно 0.

3. Градиент ⊥ линиям уровня.

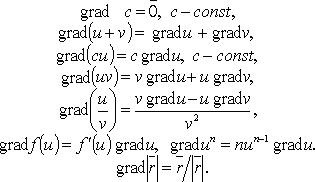
Доказательство:

нету

Теорема о необходимом условии существования локального экстремума функции двух

Переменных.

Если функция z = z(x;y) дифференцируема в точке M0(x0;y0) и имеет в этой точке локальный экстремум, то все частные производные первого порядка обращаются в этой точке в нуль:

∂Z / ∂Y = ∂Z / ∂X = 0 (в т. М0)

Доказательство:

Докажем, например, равенство нулю частной производной ∂Z / ∂X.

Зафиксируем значения переменных Y, положив их соответственно равными Y0.

Тогда функция z =z (x0;y0) является функцией одной переменной X;

Эта функция имеет в точке X = X0 локальный экстремум и производную по аргументу X, которая и является частной производной ∂Z / ∂X.

Напомним, что согласно теореме Ферма, если дифференцируемая функция одной переменной X имеет в точке X0 локальный экстремум, то ее производная в этой точке равна нулю. Аналогично доказывается равенство нулю остальных частных производных.

Теорема: необходимый признак дифференцируемости ФНП (существование всех частных

Производных).

Если функция u = f(M) = (x1, x2,.., xm) дифференцируема в т. M0(x10, x20,.., xm0), то существуют частные производные ∂U / ∂Xi , (i = 1,..,m) причем Ai = ∂U / ∂Xi * (x10, x20,.., xm0)

Доказательство:

Докажем, что в т. M0(x10, x20,.., xm0) существует ∂U / ∂X1 = A1 ∆X2 = ∆X3 = ∆Xm = 0.

f(X10+∆X1, X20, Xm0) – f(x10,…,Xm0) = A1 * ∆X1 + E(∆X1, 0, …, 0) * (∆X1)^2,

но lim E(∆X1,…, ∆Xm) = 0 (∆X1 -> 0; ∆Xm -> 0);

Значит, lim E(∆X1, 0, …, 0) =0 (аналог предела по направлению для функции m переменных)

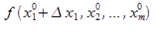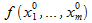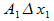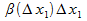– = + , где .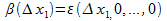

( – )/

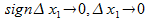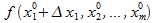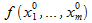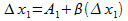
Тогда в пределе при 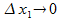существует 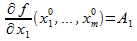что и требовалось доказать.

Теорема о дифференцируемости параметрически заданной функции ФНП.

Нету и не надо

Теорема о непрерывности дифференцируемой ФНП в точке.

Если 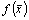– дифференцируемая в точке 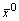ФНП, то она
непрерывна в точке .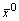

Доказательство:

По определению дифференцируемости ФНП в точке имеем ,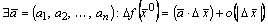

где , .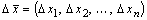

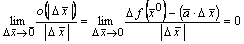При 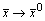, т.е. при 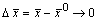, имеем 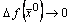, т.е. ,

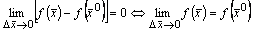что подтверждает непрерывность ФНП 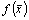в точке .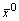