Возведение в степень и извлечение корня
Возможность представления комплексного числа в показательной форме позволяет возводить комплексное число в степень – целую или дробную.
Рассмотрим функцию 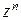 , задав число
, задав число 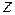 в показательной форме:
в показательной форме: 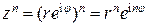 . Таким образом, при возведении комплексного числа в степень n получим новое комплексное число с модулем, равным модулю исходного числа в n-й степени и аргументом, равным аргументу исходного числа, умноженному на n.
. Таким образом, при возведении комплексного числа в степень n получим новое комплексное число с модулем, равным модулю исходного числа в n-й степени и аргументом, равным аргументу исходного числа, умноженному на n.
При извлечении корня степени n также используем показательную форму записи комплексного числа, но при этом отметим, что уравнение 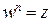 при любой правой части имеет ровно n комплексных корней.
при любой правой части имеет ровно n комплексных корней.
Действительно, если вместо 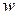 взять
взять 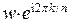 при любом целом
при любом целом 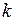 , то при возведении в степень n мы получим тот же результат, так как при любом целом значении
, то при возведении в степень n мы получим тот же результат, так как при любом целом значении 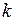 справедливо равенство
справедливо равенство 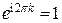 . Поскольку
. Поскольку 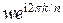 и
и 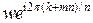 при любом целом m – это одно и то же комплексное число, имеет смысл брать
при любом целом m – это одно и то же комплексное число, имеет смысл брать 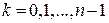 . Поэтому при извлечении корня из комплексного числа
. Поэтому при извлечении корня из комплексного числа 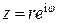 представим его в виде
представим его в виде 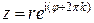 , где
, где 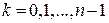 . Тогда
. Тогда 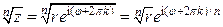 ,
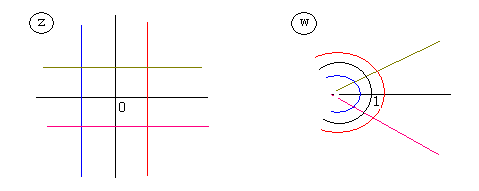
, 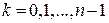 , то есть мы получим n различных корней, имеющих одинаковый модуль, но разные аргументы. Два корня с соседними значениями
, то есть мы получим n различных корней, имеющих одинаковый модуль, но разные аргументы. Два корня с соседними значениями 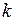 отличаются друг от друга аргументами, разность между которыми
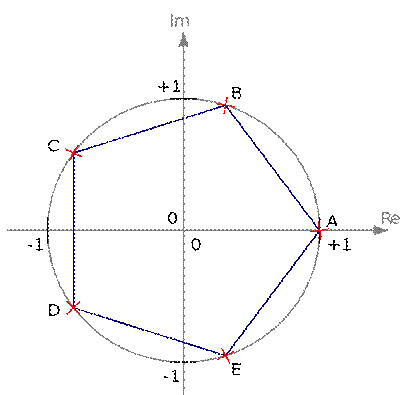
отличаются друг от друга аргументами, разность между которыми 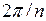 . Следовательно, все корни из одного и того же комплексного числа находятся на окружности с центром в нуле радиуса
. Следовательно, все корни из одного и того же комплексного числа находятся на окружности с центром в нуле радиуса 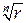 и представляют собой вершины правильного n-угольника, вписанного в эту окружность.
и представляют собой вершины правильного n-угольника, вписанного в эту окружность.
Заметим, что обобщением того свойства, что уравнение 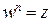 имеет ровно n комплексных корней, является знаменитая основная теорема алгебры, в соответствии с которой любое уравнение n-й степени вида
имеет ровно n комплексных корней, является знаменитая основная теорема алгебры, в соответствии с которой любое уравнение n-й степени вида 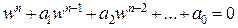 имеет ровно n корней в множестве комплексных чисел, правда в этом случае корни могут быть кратными (совпадать).
имеет ровно n корней в множестве комплексных чисел, правда в этом случае корни могут быть кратными (совпадать).
Показательная функция, тригонометрические функции
И обратные к ним
1. Показательная функция 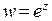 определена и однозначна во всей комплексной плоскости. Если комплексное число
определена и однозначна во всей комплексной плоскости. Если комплексное число 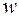 записать в показательной форме:
записать в показательной форме: 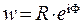 , а комплексное число
, а комплексное число 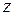 записать в алгебраической форме:
записать в алгебраической форме: 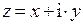 , то согласно соотношению
, то согласно соотношению 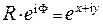 и формуле Эйлера получим
и формуле Эйлера получим 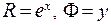 .
.
2. Тригонометрические функции представляются с помощью показательной функции благодаря формуле Эйлера. Поскольку согласно формуле Эйлера 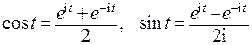 , соответствующие функции комплексного переменного так и определяются:
, соответствующие функции комплексного переменного так и определяются: 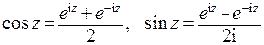 .
.
Обе эти функции определены и однозначны для всех точек комплексной плоскости.
Тангенс и котангенс комплексного переменного вводятся так же, как и для вещественного переменного: 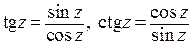 .
.
3. Функция, обратная к показательной, называется, как и в случае вещественного переменного, логарифмической функцией и обозначается 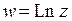 . Она определена всюду в комплексной плоскости, кроме точки
. Она определена всюду в комплексной плоскости, кроме точки 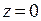 . Однако теперь это функция, имеющая бесконечное множество значений. Действительно, как уже было отмечено,
. Однако теперь это функция, имеющая бесконечное множество значений. Действительно, как уже было отмечено, 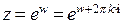 для любого целого значения числа
для любого целого значения числа 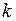 . Поэтому одному значению комплексного числа
. Поэтому одному значению комплексного числа 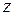 соответствует бесконечное множество значений
соответствует бесконечное множество значений 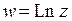 , отличающихся на слагаемое
, отличающихся на слагаемое 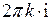 . Представим число
. Представим число 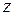 в показательной форме:
в показательной форме: 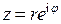 , а число
, а число 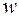 в алгебраической форме:
в алгебраической форме: 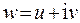 . Тогда
. Тогда 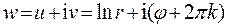 . То есть,
. То есть, 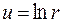 , где логарифм положительной функции – известная со школьных времен однозначная функция вещественного переменного,
, где логарифм положительной функции – известная со школьных времен однозначная функция вещественного переменного, 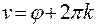 . Для того, чтобы избавиться от неоднозначности логарифма, рассматривают функцию
. Для того, чтобы избавиться от неоднозначности логарифма, рассматривают функцию 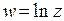 – однозначную ветвь логарифма, договариваясь, какие значения принимает мнимая часть функции. Заметим, что функцию комплексного переменного
– однозначную ветвь логарифма, договариваясь, какие значения принимает мнимая часть функции. Заметим, что функцию комплексного переменного 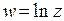 можно рассматривать только в такой области комплексной плоскости, где невозможно обойти вокруг точки
можно рассматривать только в такой области комплексной плоскости, где невозможно обойти вокруг точки 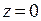 , иначе функция перестанет быть однозначной.
, иначе функция перестанет быть однозначной.
Заметим, что теперь мы можем вычислять логарифм отрицательного числа. Например, 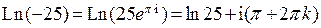 .
.
4. Для того, чтобы вычислить обратную тригонометрическую функцию, следует решить соответствующее уравнение. Например, следует вычислить функцию, обратную к синусу 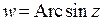 . Запишем:
. Запишем: 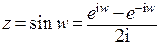 . Теперь решим уравнение
. Теперь решим уравнение 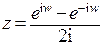 относительно
относительно 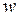 . Имеем
. Имеем 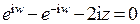 или
или 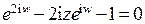 . Это квадратное уравнение относительно
. Это квадратное уравнение относительно 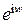 , решим его:
, решим его: 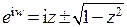 . Теперь
. Теперь 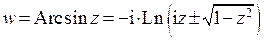 . Очевидно, что раз в представлении арксинуса содержится бесконечнозначная функция
. Очевидно, что раз в представлении арксинуса содержится бесконечнозначная функция 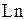 , функция
, функция 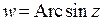 также бесконечнозначна.
также бесконечнозначна.
