Теорема Больцано-Вейерштрасса

Теорема. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Доказательство. Так как последовательность ограничена, то она имеет хотя бы одну предельную точку x. В таком случае из этой последовательности можно выделить подпоследовательность, сходящуюся к точке x.

Замечание 1. Из любой ограниченной последовательности можно выделить монотонную подпоследовательность.

В самом деле, в силу теоремы Больцано-Вейерштрасса из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность, а из этой подпоследовательности можно выделить монотонную подпоследовательность.

Замечание 2. Пусть {x_n} - ограниченная последовательность, элементы которой находятся в сегменте [a, b]. Тогда предел с любой сходящейся подпоследовательности 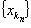также находится на сегменте [a, b].

Действительно, так как 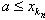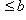, то в силу следствия 2 выполняются неравенства a ≤ c ≤ b. Это и означает, что c находится на сегменте [a, b].

Отметим, что в отдельных случаях и из неограниченной последовательности также можно выделить сходящуюся подпоследовательность. Например, последовательность 1, 1/2, 2, 1/3, ..., n, 1/(n+1), ... неограниченная, однако подпоследовательность 1/2, 1/3, ..., 1/n, ... ее элементов с четными номерами сходится. Но не из каждой неограниченной последовательности можно выделить сходящуюся подпоследовательность. Например, любая подпоследовательность неограниченной последовательности 1, 2, ..., n, ... расходится. Поэтому теорему Больцано-Вейерштрасса, вообще говоря, нельзя распространить на неограниченные последовательности.

Критерий Коши. Функция f имеет конечный предел в точке x₀ тогда и только тогда, когда

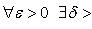
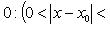
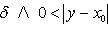
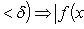
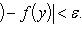
Особую роль играют два замечательных предела:

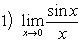
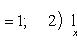
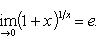
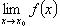
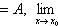
Если 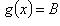, то

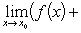
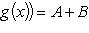
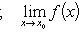
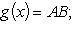
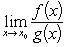
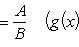
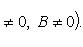
34.

ОДНОСТОРОННИЙ ПРЕДЕЛ

- предел функции в нек-рой точке справа или слева. Пусть f - отображение упорядоченного множества X(напр., множества, лежащего на числовой прямой), рассматриваемого как топологич. пространство с топологией, порожденной отношением порядка, в топологич. пространство Y и . Предел отображения f по любому интервалу 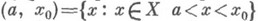наз. пределом слева отображения f и обозначают

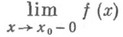
(он не зависит от выбора 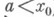), а предел по интервалу 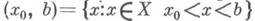наз. пределом справа и обозначают

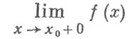
(он не зависит от выбора 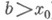). Если точка 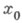является предельной как слева, так и справа для множества определения функции f, то обычный предел

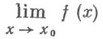
по проколотой окрестности точки х ₀ (в этом случае его наз. также двусторонним, в отличие от односторонних пределов) существует тогда и только тогда, когда в точке х ₀ существуют пределы слева и справа и они равны между собой.

Преде́л фу́нкции — одно из основных понятий математического анализа. Функция 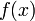имеет предел 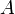в точке 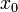если для всех значений 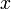, достаточно близких к 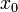, значение 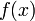близко к .

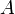35.