Локальные экстремумы функции нескольких переменных

Точка называется точкой локального максимума функции , если существует интервал , содержащий точку такой что .

Точка называется точкой локального минимума функции , если существует интервал , содержащий точку такой что .

Точки локального минимума и локального максимума называются точками локального экстремума.

Необходимым условием локального экстремума дифференцируемой функции является выполнение равенства . Поэтому точки, в которых дифференцируемая функция может иметь локальный экстремум,

Пусть функция определена и непрерывна в области. Локальным максимумом этой функции называется внутренняя точка, у которой существует такая ненулевая– окрестность для каждой точки, из которой выполняется условие: .

Если каждой точки из ненулевой – окрестности точки выполняется условие, то точка называется локальным минимумом функции.\Точки локального минимума или максимума называются точками локального экстремума. Для этих точек характерно знакопостоянство величины абсолютного приращения в пределах ненулевой – окрестности. Для определения необходимого и достаточного признаков экстремальности функции предположим, что функция в области не имеет точек разрыва и обладает дифференцируемостью до второго порядка. Как было указано выше, разложение абсолютного приращения имеет вид

Главный член разложения полного приращения является знакопеременным, так как линейно зависит от приращений . Поэтому в точке у функции не может наблюдаться экстремума, если вектор–градиент этой функции точке будет отличен от нулевого вектора, т.е. хотя бы одна из частных производных не будет равна нулю. Таким образом, необходимым условием существования локального экстремума функции является условие или

Точки, в которых первые частные производные функции равны нулю или не существуют, называются критическими для данной функции. Критические точки, в которых первые частные производные функции существуют, называются стационарными. Функция многих переменных может достигать своего локального экстремума только в своей критической точке.

При обосновании достаточного условия существования экстремума введем дополнительное требование к функции: эта функция должна иметь непрерывные производные второго порядка в ненулевой – окрестности точки . Тогда условием наличия локального экстремума в критической точке или условием знакопостоянства абсолютного приращения в этой точке будет требование знакопостоянства второго слагаемого в разложении , т.е. . Влияние третьего и последующих членов разложения в этом случае будет пренебрежимо малым. Если формулу для вычисления сгруппировать и представить в виде квадратичной формы:

,

то требование знакопостоянства сводится к требованию знакоопределенности матрицы квадратичной формы в критической точке . В этом случае, если матрица квадратичной формы является положительно определенной, то в точке функция имеет локальный минимум, а если матрица отрицательно определена – то локальный максимум.

Условие знакопостоянства полного относительного приращения выполняется в точках локальной выпуклости, определение которых можно дать по аналогии с функциями одной переменной.

Точка называется точкой локальной выпуклости функции , непрерывной и дифференцируемой в области , если она является внутренней точкой этой области и в некоторой ненулевой –окрестности точки выполняется условие: полное относительное приращение знакопостоянно.

Если , точка называется точкой выпуклости вниз.

Если , точка называется точкой выпуклости вверх.

Если условие локальной выпуклости вверх или вниз выполняется во всех точках области , то функция называется однообразно выпуклой на области .

Достаточным условием существования локальной выпуклости функции нескольких переменных в точке является знакопостоянство полного дифференциала второго порядка этой функции. Это несложно показать, воспользовавшись формулой разложения:

и проведя рассуждения аналогичные доказательству достаточного условия существования локального экстремума. Таким образом, знакопостоянство полного относительного приращения функции в некоторой ненулевой –окрестности точки определяется знакопостоянством полного второго дифференциала функции в точке .

Если , то функция имеет в точке локальную выпуклость вниз. Если , то функция имеет в точке локальную выпуклость вверх. Достаточное условие существования локального экстремума в критической точке кроме необходимого признака включает в свой состав требование наличия локальной выпуклости в этой точке.

Функция u = f(M) имеет в точке 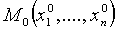локальный максимум (минимум), если существует такая окрестность точки 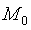, для всех точек 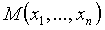которой, отличных от 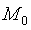,выполняется неравенство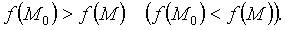

Необходимое условие экстремума:

Если дифференцируемая функция u = f(M) достигает экстремума в точке 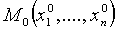, то

Точки, в которых выполняется (9.2), называют стационарными.

Достаточное условие экстремума:

Пусть 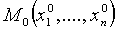- стационарная точка функции. Предположим, что функция u = f(x) дважды непрерывно дифференцируема в окрестност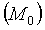и и 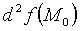- значение второго дифференциала в точке 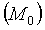, то есть

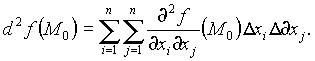
Легко заметить, что 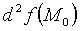является квадратичной формой относительно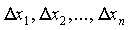

Тогда:

1. Если 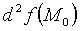, как функция 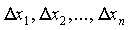имеет постоянный знак при всевозможных наборах 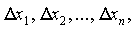значений не равных нулю одновременно, то функция имеет в точке 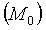экстремум, а именно максимум, при 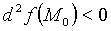и минимум при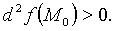

2. Если 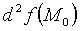является знакопеременной функцией 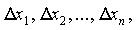то есть принимает как положительные так и отрицательные значения, то точка 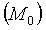не является точкой экстремума.

3. Ес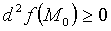ли или 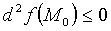, причём существуют такие 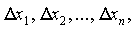при которых 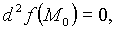то функция u = f(M) в точке 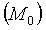может иметь экстремум, а может и не иметь. В этом случае можно провести дополнительное исследование.

Что бы выяснить будет ли квадратичная форма

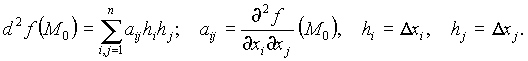
знакопостоянной, применяют критерий Сильвестра.

Положим,

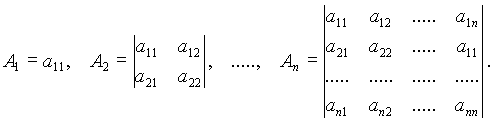
1. Для того, чтобы 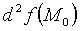была знакоположительна, то есть 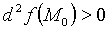при любых наборах 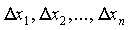необходимо и достаточно, чтобы выполнялись неравенства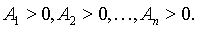

2. Для того, чтобы 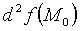была знакоотрицательна, то есть 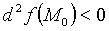при любых наборах 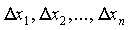необходимо и достаточно, чтобы знаки чисел 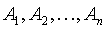чередовались, причём 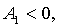т.е.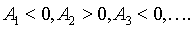

Применим критерий Сильвестра для случая функции двух переменных z = f(x, y). Положим

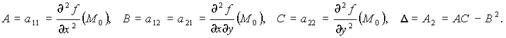
Тогда:

1. Если 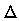> 0, то функция z = f(x, y) имеет в точке 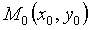экстремум, а именно максимум при A < 0 (C < 0) и минимум при A > 0 (C > 0).

2. Если 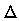< 0, то функция z = f(x, y) в точке экстремума 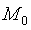не имеет.

3. Если 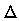= 0, то для решения вопроса об экстремуме в точке 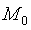требуется дополнительное исследование.

Пример решений

Пример 8.1. Исследовать на экстремум функции

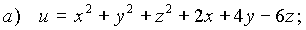
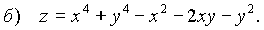
Решение. а) Определим стационарные точки из системы

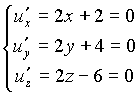
Откуда имеем единственную стационарную точку: х = - 1, у = - 2, z = 3. Воспользуемся достаточным условием

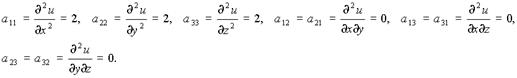
Таким образом,

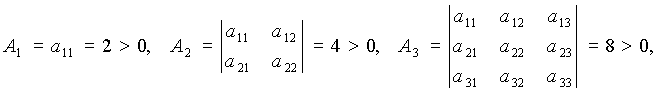
то есть, согласно критерию Сильвестра, 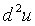представляет собой положительно определённую квадратичную форму. Следовательно, в точке 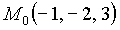функция имеет минимум.

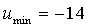
б) Находим,

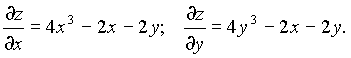
Стационарные точки определяются из системы

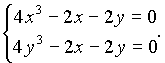
Она имеет три решения 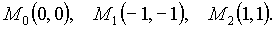Для применения достаточных условий локального экстремума вычислим вторые производные

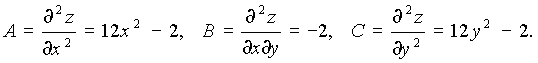
Составим выражение 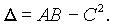В точке 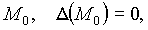следовательно, необходимы дополнительные исследования.

Рассмотрим 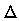z(0, 0) = z(h, k) - z(0, 0).

При 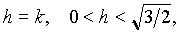имеем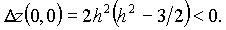

При 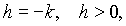имеем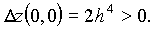

Таким образом, приращение 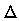z(0, 0) принимает значения разных знаков, а поэтому в точке 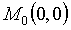экстремума нет.

Далее в точках 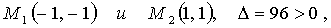и так как 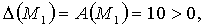то в этих точках достигается минимум, причём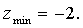

Пример 8.2. На плоскости даны n точек 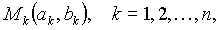в которых сосредоточенны массы 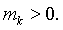Требуется найти на этой плоскости точку 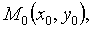такую относительно которой момент инерции указанной системы материальных точек минимален.

Решение. Момент инерции относительно точек равен

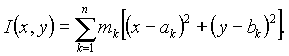
Таким образом, задача сводится к отысканию точки 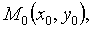в которой функция I(x, y) достигает своего минимума.

Имеем

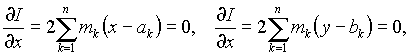
откуда единственной стационарной точкой будет точка с координатами

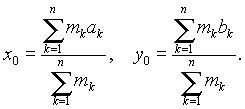
Далее, так как

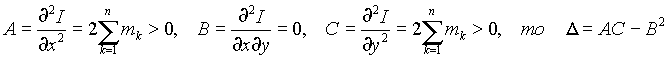
и значит функция I(x, y) имеет в точке 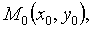локальный минимум.

Нетрудно увидеть, что значение функции I(x, y) в этой точке является минимальным.