Собственные значения и собственные векторы
Собственным вектором линейного оператора (матрицы)
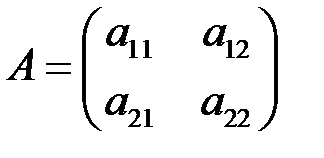 ,
,
соответствующим собственному значению 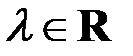 называется ненулевой вектор
называется ненулевой вектор 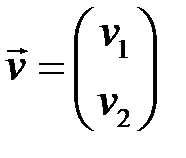 такой, что
такой, что
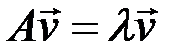 . (6.2)
. (6.2)
Таким образом, линейный оператор преобразует свой собственный вектор 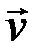 в вектор ему коллинеарный (сонаправленный с
в вектор ему коллинеарный (сонаправленный с 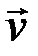 при
при 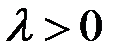 и противоположно направленный при
и противоположно направленный при 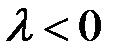 ). Любой ненулевой вектор
). Любой ненулевой вектор 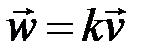 , коллинеарный собственному вектору
, коллинеарный собственному вектору 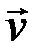 , также является собственным, соответствующим тому же собственному значению
, также является собственным, соответствующим тому же собственному значению 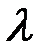 :
:
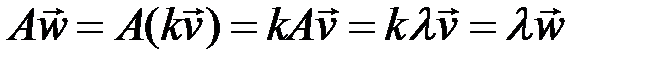 .
.
В координатах равенство (6.2) имеет вид
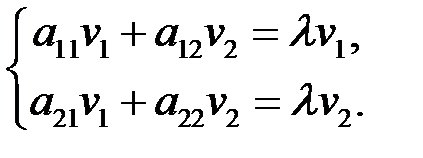

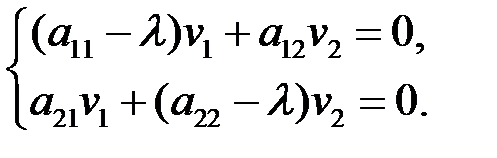 (6.3)
(6.3)
Это система линейных уравнений относительно координат 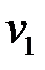 ,
, 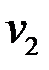 собственного вектора. Она имеет ненулевое решение, если определитель системы равен нулю:
собственного вектора. Она имеет ненулевое решение, если определитель системы равен нулю:
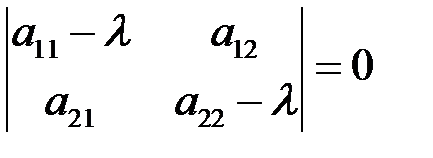

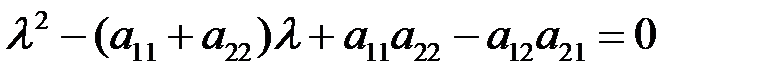 . (6.4)
. (6.4)
Таким образом, для нахождения собственных значений получили квадратное уравнение (6.4). Оно называется характеристическим уравнением. Найдя из него собственное значение 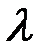 , надо подставить его в (6.3). Решив полученную систему линейных уравнений, найдем координаты
, надо подставить его в (6.3). Решив полученную систему линейных уравнений, найдем координаты 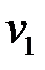 и
и 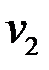 собственного вектора, соответствующего собственному значению
собственного вектора, соответствующего собственному значению 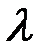 .
.
Если характеристическое уравнение не имеет действительных корней, то линейный оператор не имеет собственных векторов. Например, их нет у оператора поворота на угол 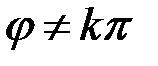 ,
, 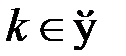 .
.
Аналогично, формула (6.2) определяет собственный вектор 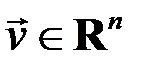 , соответствующий собственному значению
, соответствующий собственному значению 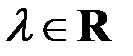 , для квадратной матрицы
, для квадратной матрицы 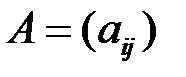
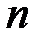 -го порядка (линейного оператора в
-го порядка (линейного оператора в 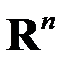 ) при любом
) при любом 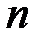 . Собственные значения находятся из характеристического уравнения
. Собственные значения находятся из характеристического уравнения
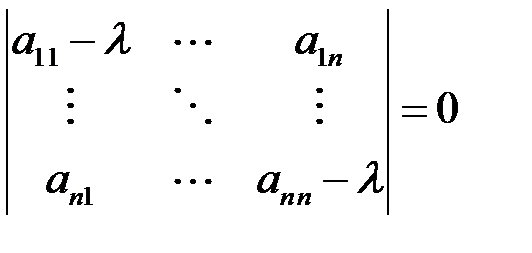

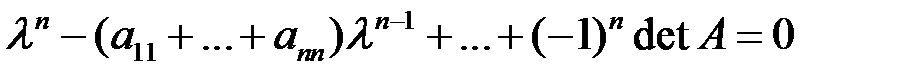 .
.
Для каждого собственного значения 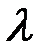 координаты
координаты 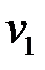 ,…,
,…, 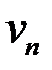 соответствующего собственного вектора
соответствующего собственного вектора 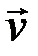 находятся из системы линейных уравнений
находятся из системы линейных уравнений
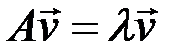

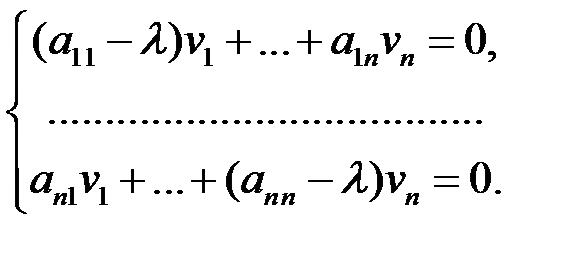
Примеры решения задач
6.2.1.Дана матрицалинейного оператора 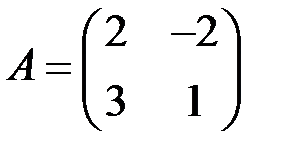 . Записать равенство
. Записать равенство 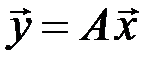 в координатной форме.
в координатной форме.
◄ По определению (формула (6.2))
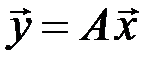

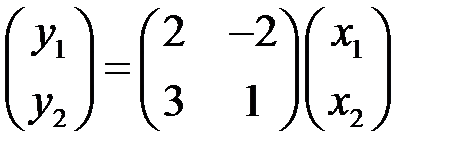

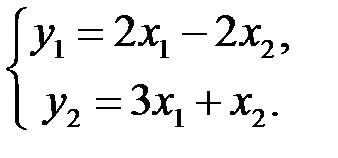 ►
►
6.2.2.Найти вектор 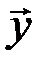 , в который линейный оператор
, в который линейный оператор 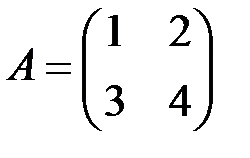 преобразует вектор
преобразует вектор 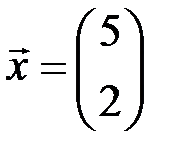 .
.
◄ Линейный оператор 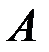 преобразует вектор
преобразует вектор 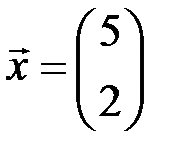 в его образ
в его образ
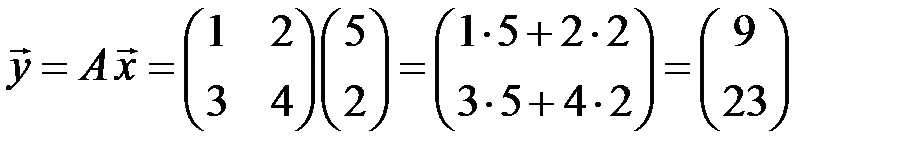 . ►
. ►
6.2.3.Найти собственные значения и собственные векторы линейного оператора (матрицы) 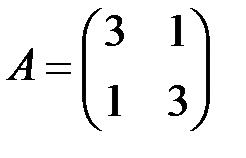 .
.
◄ Собственные значения 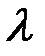 находим из характеристического уравнения (6.4):
находим из характеристического уравнения (6.4):
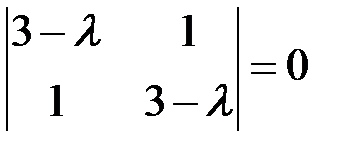

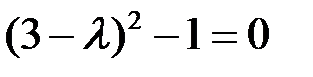

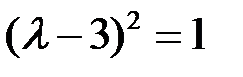

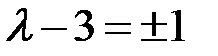 ,
,
корни которого 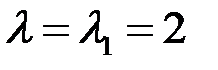 и
и 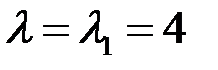 .
.
Система (6.3) для нахождения координат 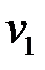 и
и 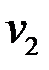 собственных векторов в рассматриваемом случае имеет вид
собственных векторов в рассматриваемом случае имеет вид
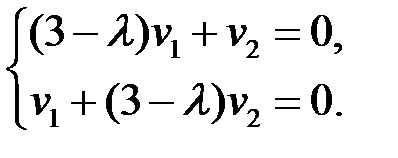 (6.5)
(6.5)
Подставим в нее 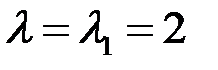 :
:
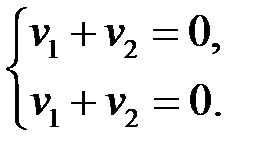
Полагая 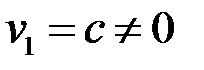 – произвольным, находим
– произвольным, находим 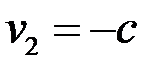 . Таким образом, векторы
. Таким образом, векторы 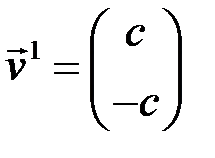 , где
, где 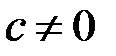 – собственные векторы, соответствующие собственному значению
– собственные векторы, соответствующие собственному значению 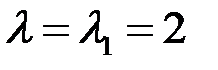 , то есть
, то есть 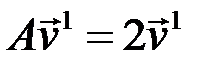 (рис 6.2).
(рис 6.2).
Подставим в (6.5) 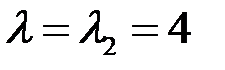 :
:
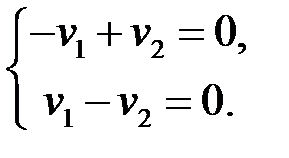
Полагая 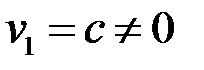 – произвольным, находим
– произвольным, находим 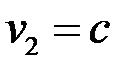 . Таким образом, векторы
. Таким образом, векторы 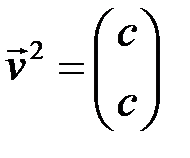 , где
, где 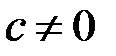 – собственные векторы, соответствующие собственному значению
– собственные векторы, соответствующие собственному значению 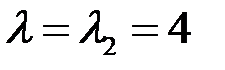 , то есть
, то есть 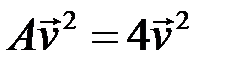 (рис 6.2) .
(рис 6.2) .
Возьмем 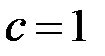 и разложим произвольный вектор
и разложим произвольный вектор 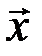 по базису из векторов
по базису из векторов 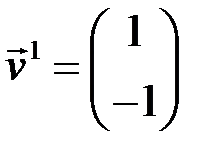 ,
, 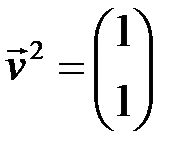 :
: 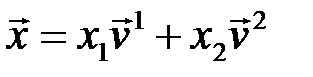 . Тогда его образ
. Тогда его образ
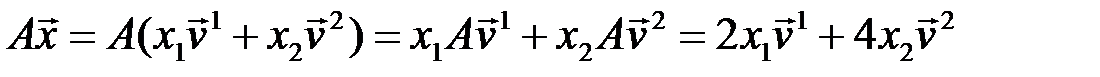 ,
,
то есть действие оператора на произвольный вектор 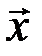 состоит в «растяжении» его по направлениям собственных векторов
состоит в «растяжении» его по направлениям собственных векторов 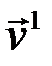 и
и 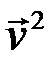 , соответственно в
, соответственно в 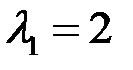 и
и 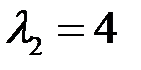 раз (рис 6.2). ►
раз (рис 6.2). ►
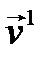 |
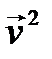 |
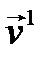 |
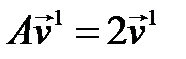 |
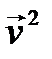 |
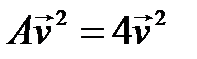 |
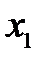 |
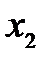 |
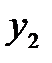 |
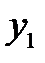 |
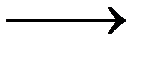 |
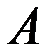 |
Рис. 6.2. Действие оператора 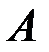 на параллелограмм, построенный на собственных векторах. на параллелограмм, построенный на собственных векторах. |
