Динамика материальной точки
1. Инерциальные системы отчёта, это такие системы отсчёта, в которых:
1) все тела движутся только по инерции;
2) действуют силы инерции;
3) выполняется I-й закон Ньютона;
4) не выполняется I-й закон Ньютона.
2. По первому закону Ньютона:
1)тело под действием постоянной силы движется равноускоренно;
2)тело, на которое не действуют силы, обязательно покоится;
3)тело, на которое не действуют силы, не изменяет своей скорости;
4)тело под действием постоянной силы движется с постоянной скоро-
стью.
3. Первый закон Ньютона:
1) постулирует существование инерциальных систем отсчёта (ИСО);
2) отвергает возможность существования ИСО;
3) провозглашает эквивалентность ИСО и неинерциальных СО;
4) определяет, что такое система отсчёта.
4. Согласно первому закону Ньютона:
1) в инерциальных системах отсчёта (ИСО) тело всегда покоится;
2) в ИСО тело имеет постоянную скорость;
3) в ИСО тело не меняет состояния, если на него не действуют силы;
4) скорость тела зависит от скорости ИСО.
5. В какой из формул отражено содержание II-го закона Ньютона?
1) 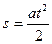 , 2)
, 2) 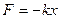 , 3)
, 3) 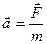 , 4)
, 4) 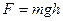 .
.
6. Если тело двигается таким образом, что ускорение 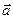 и скорость
и скорость 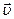 взаимно перпендикулярны, то согласно II-му закону Ньютона, действующая на тело сила:
взаимно перпендикулярны, то согласно II-му закону Ньютона, действующая на тело сила:
1) параллельна 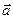 ;
;
2) параллельна 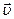 ;
;
3) параллельна сумме векторов 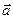 и
и 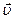 ;
;
4) параллельна разности векторов 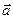 и
и 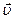 .
.
7. В какой из формул неправильно записан второй закон Ньютона:
1) 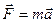 , 2)
, 2) 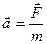 , 3)
, 3) 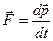 , 4)
, 4) 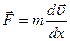 .
.
8. 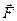 во втором законе Ньютона – это:
во втором законе Ньютона – это:
1) сумма модулей всех действующих на тело сил;
2) векторная сумма всех сил, действующих в данной задаче;
3) векторная сумма сил, действующих на одно тело;
4) сила тяги, действующая на тело.
9. Если на тело, масса которого 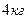 , действует одна сила, равная
, действует одна сила, равная 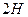 , то это тело движется с ускорением:
, то это тело движется с ускорением:
1) 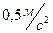 , 2)
, 2) 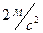 , 3)
, 3) 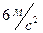 , 4)
, 4) 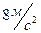 .
.
10. Если тело, масса которого 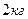 двигается по закону
двигается по закону 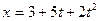 , то равнодействующая сил, действующих на него равна:
, то равнодействующая сил, действующих на него равна:
1) 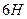 , 2)
, 2) 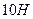 , 3)
, 3) 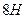 , 4)
, 4) 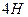 .
.
11. Если тело, масса которого 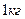 , двигается по закону
, двигается по закону 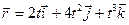 , то, в начале второй секунды модуль равнодействующей силы равен:
, то, в начале второй секунды модуль равнодействующей силы равен:
1) 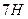 , 2)
, 2) 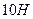 , 3)
, 3) 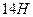 , 4)
, 4) 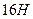 .
.
12. На столе находится брусок массой 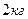 , коэффициент трения поверхности бруска о поверхность стола
, коэффициент трения поверхности бруска о поверхность стола 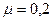 . На брусок действует сила
. На брусок действует сила 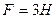 , направленная параллельно поверхности стола. В этих условиях сила трения равна:
, направленная параллельно поверхности стола. В этих условиях сила трения равна:
1) 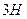 , 2)
, 2) 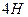 , 3)
, 3) 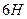 , 4)
, 4) 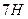 .
.
13. Если тело массой 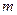 покоится, то значение силы трения оказывается равным (здесь
покоится, то значение силы трения оказывается равным (здесь 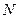 - сила нормального давления,
- сила нормального давления, 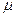 - коэффициент трения):
- коэффициент трения):
1) нулю, 2) 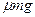 , 3)
, 3) 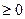 и
и 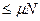 , 4)
, 4) 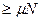 .
.
14. Если на находящейся, на поверхности стола брусок массой 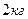 подействовать силой
подействовать силой 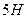 параллельно поверхности стола, то сила трения будет равна (при коэффициенте трения
параллельно поверхности стола, то сила трения будет равна (при коэффициенте трения 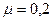 ):
):
1) 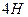 , 2)
, 2) 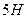 , 3)
, 3) 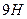 , 4)
, 4) 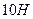 .
.
15. Сила трения относится к:
1) гравитационному взаимодействию;
2) электромагнитному взаимодействию;
3) сильному взаимодействию;
4) слабому взаимодействию.
16. Брусок, масса которого 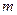 , скользит по наклонной плоскости, образующий угол
, скользит по наклонной плоскости, образующий угол 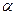 с горизонтом. Если коэффициент трения бруска о поверхность равен
с горизонтом. Если коэффициент трения бруска о поверхность равен 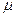 , то сила трения равна:
, то сила трения равна:
1) 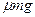 , 2)
, 2) 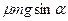 , 3)
, 3) 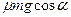 , 4)
, 4) 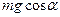 .
.
17.Плоскость, на которой лежит шайба (масса её 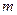 , коэффициент трения
, коэффициент трения 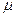 ) постепенно наклоняют, увеличивая угол
) постепенно наклоняют, увеличивая угол 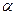 с горизонтом. В момент, когда шайба начнёт движение на неё действует сила трения равная:
с горизонтом. В момент, когда шайба начнёт движение на неё действует сила трения равная:
1) 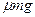 , 2)
, 2) 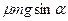 , 3)
, 3) 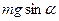 , 4)
, 4) 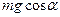 .
.
18. Груз массой 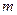 привязан к нити, намотанной на блок, который может свободно вращаться. Если груз отпустить, то он будет опускаться с ускорением
привязан к нити, намотанной на блок, который может свободно вращаться. Если груз отпустить, то он будет опускаться с ускорением 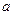 . Сила натяжения нити при этом равна:
. Сила натяжения нити при этом равна:
1) 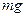 , 2)
, 2) 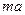 , 3)
, 3) 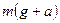 , 4)
, 4) 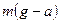 .
.
19. По закону Гука, при растяжении пружины, жёсткость которой 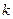 , на
, на 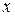 м, возникающая сила упругости равна:
м, возникающая сила упругости равна:
1) 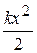 , 2) -
, 2) - 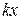 , 3)
, 3) 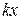 , 4) -
, 4) - 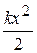 .
.
20. Жесткость 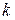 в законе Гука имеет размерность:
в законе Гука имеет размерность:
1) 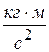 , 2)
, 2) 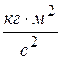 , 3)
, 3) 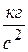 , 4)
, 4) 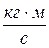 .
.
21. Модуль Юнга 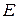 связан с жёсткостью
связан с жёсткостью 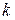 соотношением:
соотношением:
1) 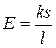 , 2)
, 2) 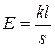 , 3)
, 3) 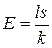 , 4)
, 4) 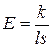 .
.
22. Единицы, используемые для измерения модуля Юнга:
1) 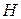 , 2)
, 2) 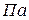 , 3)
, 3) 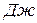 , 4)
, 4) 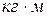 .
.
23. Жесткость 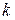 в законе Гука связана с модулем Юнга
в законе Гука связана с модулем Юнга 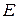 соотношением (l-длина,
соотношением (l-длина, 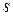 - площадь поперечного сечения образца):
- площадь поперечного сечения образца):
1) 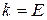 , 2)
, 2) 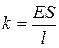 , 3)
, 3) 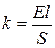 , 4)
, 4) 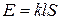 .
.
24. Сила упругости относится к:
1) гравитационному взаимодействию;
2) электромагнитному взаимодействию;
3) сильному взаимодействию;
4) слабому взаимодействию.
25. Согласно третьему закону Ньютона:
1) силы, действующие на тело, уравновешивают друг друга;
2) при взаимодействии двух тел сила действия первого тела на
второе равна силе действия второго тела на первое;
3) силы трения всегда уравновешивают силы тяги;
4) силы упругости всегда уравновешивают силу тяжести.
