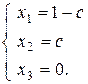Задачи для самостоятельного решения. б) Решить матричное уравнение АХ =В, где

а) Найти А^-1, где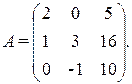

б) Решить матричное уравнение АХ =В, где

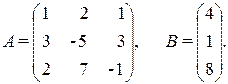
РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ

Линейные системы уравнений

Дана система m уравнений с n неизвестными

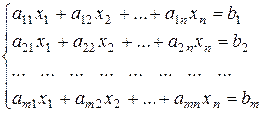. (3.1)

Решением этой системы называется любая совокупность n чисел (a₁, a₂,..., a_n), которая при подстановке в систему вместо совокупности неизвестных обращает каждое уравнение системы в тождество. Система (3.1) называется совместной, если она имеет хотя бы одно решение. В противном случае она называется несовместной..

Матрицы

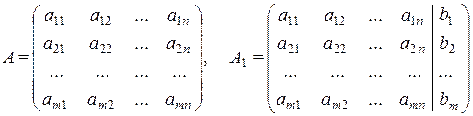
называются соответственно матрицей и расширенной матрицей

системы (3.1).

Исследование на совместность и решение системы производят обычно одновременно с помощью метода Гаусса. Напомним, что элементы а_ii в матрице А называются диагональными. Метод Гаусса заключается в элементарных преобразованиях строк матрицы А₁ так, чтобы элементы преобразованной матрицы, стоящее ниже диагональных элементов, были нулевыми. При этом необходимо следить за диагональными элементами: они не должны обращаться в нуль. Если же при элементарных преобразованиях строк какой-либо диагональный элемент обратится в нуль (например, а_ii = 0), то поступать необходимо следующим образом: а) если в этом же столбце (где диагональный элемент оказался равен нулю) имеется ниже диагонального элемента ненулевой элемент, то соответствующую строку меняют местом с i-й строкой и продолжают преобразования; б) если же ниже нулевого диагонального элемента все элементы нулевые, то мы должны перейти к построению ступенчато-диагональной матрицы. Для этого сдвигаемся на один столбец вправо и считаем, что и диагональ матрицы тоже сдвинулась вправо и далее поступаем как описано выше. После всех преобразований матрица системы должна принять так называемый диагонально ступенчатый вид:

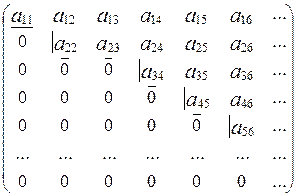
Ступенек в преобразованной матрице может быть несколько, причем разной длины. Элементы, которые будут стоять в углах таких ступенек, назовем ступенчато-диагональными (в данном примере это: а₁₁, а₂₂, а₃₄, а₄₅, а₅₆, ...).

Примеры.

а) Проверим совместность системы

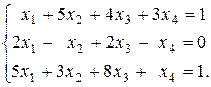
Для этого запишем расширенную матрицу системы и проведем элементарные преобразования над строками:

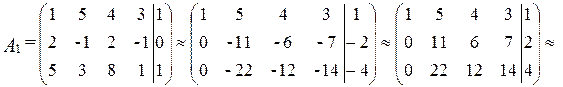
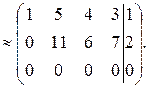
Из сказанного выше вытекает, что данная система совместна.

б) Исследуем на совместность систему

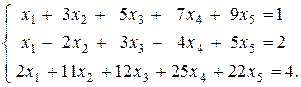
Записав расширенную матрицу системы, с помощью элементарных преобразований получаем

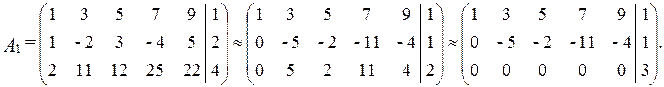
Таким образом, данная система несовместна.

Решение системы уравнений

После выяснения совместности системы строят ее общее решение. Для этого вновь полученную после элементарных преобразований матрицу записывают в виде системы, отбросив нулевые строки. Количество уравнений в этой системе определяет количество основных неизвестных. Все остальные неизвестные считаются свободными, им придаются произвольные значения. В качестве основных неизвестных берут неизвестные при ступенчато-диагональных элементах.

Примеры.

а) Построим общее решение системы из первого примера предыдущего пункта. После элементарных преобразований (см. выше) получаем систему

.

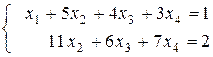Уравнений два, поэтому считаем х₁ и х₂ (стоящие при ступенчато-диаго-нальных элементах) основными, а х₃ и х₄ свободными. Находим из системы основные неизвестные через свободные:

,

.

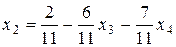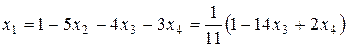Таким образом, общее решение системы имеет вид:

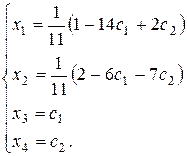
б) Решим систему

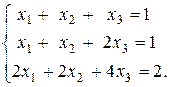
Записываем расширенную матрицу системы и преобразуем ее

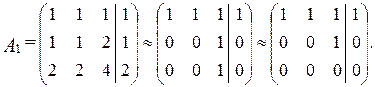
Выбираем в качестве основных переменные х₁ и х₃, как стоящие при ступенчато-диагональных элементах, переменная х₂ берется свободной. Итак,

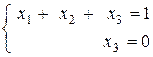
и общее решение системы