Признаки сходимости числовых рядов
1. Необходимый признак сходимости ряда.
Общий член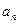 
сходящегося ряда стремится к нулю при 
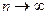. Если 
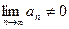, то ряд 
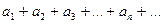расходится (необходимый признак не выполняется). Если 
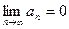, то вопрос о сходимости ряда исследуется по достаточному признаку.
Например в ряде:
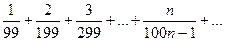(2)
;
,
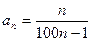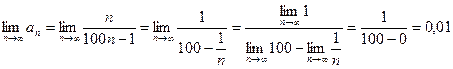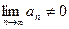
Следовательно, необходимый признак не выполняется и данный ряд расходится.
2. Достаточные признаки сходимости числовых рядов с положительными членами.
Признак Даламбера.
Пусть все члены ряда (1) 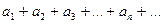- положительны и пусть при неограниченном возрастании n предел отношения (n+1)-го члена к n – му существует и равен числу l. В таком случае:
если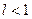 
, то ряд (1) сходится;
если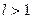 
, то ряд (1) расходится;
если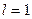 
, то признак определенного ответа не дает, так как в этом случае одни ряды сходятся, а другие расходятся.
Например. При помощи признака Даламбера исследовать расходимость ряда
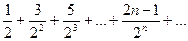(3)
Решение.
Общий член ряда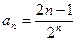 
(4)
Находим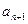 
, для чего в (4) подставим n+1 вместо n:
.
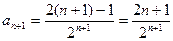Находим отношение (n+1)-го члена к n-му:
.
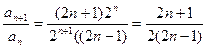Находим предел этого соотношения при :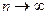
.
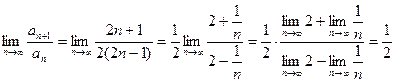Так как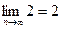 
, а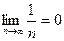 
.
Сравниваем полученный результат с единицей: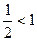 
, то есть ряд (3) сходится, так как .
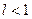Ответ: Ряд сходится.
Вопросы для самопроверки, при подготовке к экзамену.
1.Дайте определение комплексного числа.
2. Дайте определение мнимой единице.
3. Как найти степень мнимой единицы?
4. Какие комплексные числа называются равными, сопряженными?
5. Как изображаются комплексные числа геометрически?
6. Дайте определение модуля и аргумента комплексного числа.
7. Перечислите формы записи комплексного числа.
8. Какие действия выполняются над комплексными числами в алгебраической форме и приведите примеры.
9. Как выполняются действия над комплексными числами в тригонометрической форме?
10. Как выполняются действия над комплексными числами в показательной форме?
11. Что такое матрица, виды матриц.
12. Как находят определители второго и третьего порядка.
13. Что такое минор, алгебраическое дополнение элементов определителя?
14. Какие линейные операции можно выполнять над матрицами?
15. Как выполняется умножение матриц?
16. Какая матрица называется обратной по отношению данной матрице?
17. Дать определение системы линейного уравнения с n переменными.
18. Перечислить способы решения системы линейных уравнений с n переменными.
19. Объяснить сущность метода Гаусса (метода последовательного исключения переменных).
20. Как решить систему двух линейных уравнений с двумя переменными и систему трех линейных уравнений с тремя переменными по формулам Крамера?
21. Дать определение матричного уравнения и объяснить метод решения матричных уравнений.
22. Что называется вектором, абсолютной величиной вектора, направлением вектора, нулевым вектором в пространстве?
23. Дайте определение компланарных векторов.
24. Дайте определение равных векторов.
25. Как найти координаты вектора, заданного парой несовпадающих точек?
26. Как найти абсолютную величину (длину) вектора в пространстве.
27. Напишите формулу для вычисления угла между двумя векторами в пространстве.
28. Напишите формулу для вычисления скалярного произведения двух векторов по их координатам.
29. Сформулируйте условие перпендикулярности двух векторов.
30. Каков смысл предела функции в точке.
31. Сформулируйте основные свойства предела функции в точке.
32. Какие замечательные пределы Вы знаете.
33. Дайте определение производной функции.
34. В чем состоит геометрический смысл производной.
35. В чем состоит физический смысл производной?
36. Напишите таблицу производных элементарных функций.
37. Напишите все формулы дифференцирования.
38. Дать определение второй производной функции.
39. В чем состоит физический смысл второй производной?
40. Дайте определение дифференциала функции и формулы его вычисления.
41. Сформулируйте условие возрастания и убывания функции.
42. Сформулируйте необходимое условие существования экстремума функции.
43. Сформулируйте достаточное условие существования экстремума функции.
44. Сформулируйте условия выпуклости функции.
45. Какая точка называется точкой перегиба графика функции.
46. Какое действие называется интегрированием?
47. Какая функция называется первообразной?
48. Дайте определение неопределенного интеграла.
49. Перечислить основные свойства неопределенного интеграла.
50. Каким действием можно проверить интегрирование?
51. Напишите основные табличные интегралы.
52. Дать определение определенного интеграла.
53. Перечислить основные свойства определенного интеграла.
54. В чем заключается геометрический смысл определенного интеграла?
55. Напишите формулы для определения площади плоской фигуры с помощью определенного интеграла.
56. Какое уравнение называется дифференциальным?
57.. Дать определение дифференциального уравнения с разделяющимися переменными и метод его решения.
58. Дать определение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами и метод его решения.
59. Дайте определение числового ряда.
60. Что называется остатком ряда.
61. Сформулируйте свойства рядов.
62. Сформулируйте признаки Даламбера и Коши сходимости рядов.
Вопросы, выносимые на экзамен.
1. Развитие понятия о числе. Мнимая единица. Степени мнимой единицы. Решение квадратных уравнений с отрицательным дискриминантом.
2. Алгебраическая форма комплексного числа: основные определения и соотношения.
3. Геометрическая интерпретация комплексного числа. Модуль и аргумент.
4. Действия над комплексными числами в алгебраической форме.
5. Тригонометрическая форма комплексного числа. Переход от алгебраической формы в тригонометрическую и обратно.
6. Действия над комплексными числами в тригонометрической форме.
7. Показательная форма комплексного числа. Формулы Эйлера. Переход от алгебраической формы к показательной и обратно.
8. Действия над комплексными числами в показательной форме.
9. Определители второго и третьего порядка. Вычисление. Определители nго порядка.
10. Решение систем линейных уравнений по формулам Крамера.
11. Свойства определителей.
12. Миноры, алгебраические дополнения и их вычисление.
13. Метод Гаусса.
14. Матрицы: виды матриц, равенство матриц. Транспонирование матриц.
15. Линейные операции над матрицами.
16. Умножение матриц, свойства умножения матриц.
17. Определитель матрицы и его свойства. Миноры и алгебраические дополнения.
18. Обратная матрица. Обращение матриц второго и третьего порядка.
19. Решение простейших матричных уравнений.
20. Уравнение прямой на плоскости.
21. Условия перпендикулярности и параллельности двух прямых.
22. Формула вычисления угла между двумя прямыми на плоскости.
23. Предел функции в точке и его основные свойства.
24. Замечательные пределы.
25. Понятие производной функции. Физический смысл производной. Геометрический смысл производной. Уравнения касательной и нормали.
26. Таблица производных элементарных функций. Правила дифференцирования. Производные высших порядков.
27. Дифференциал функции и его вычисление.
28. Общая схема исследования функции методами дифференциального исчисления.
29. Первообразная, ее основное свойство и геометрический смысл.
30. Неопределенный интеграл и его свойства.
31. Таблица интегралов элементарных функций
32. Метод непосредственного интегрирования.
33. Метод подстановки.
34. Метод интегрирования по частям.
35. Интегрирование рациональных функций.
36. Интегрирование иррациональных функций.
37. Интегрирование методом универсальной подстановки.
38. Определенный интеграл, его геометрический смысл и свойства.
39. Формула Ньютона – Лейбница. Вычисление определенного интеграла методом непосредственного интегрирования.
40. Метод подстановки в определенном интеграле.
41. Вычисление площадей плоских фигур с помощью определенного интеграла.
42. Дифференциальные уравнения: основные понятия и определения.
43. Дифференциальные уравнения первого порядка. Задача Коши. Дифференциальные уравнения с разделяющимися переменными: общее и частное решения.
44. Дифференциальные уравнения второго порядка. Задача Коши. Неполные дифференциальные уравнения второго порядка и их решения.
45. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами и их решение.
46. Определение числового ряда, остаток ряда, частичная сумма ряда.
47. Признаки сравнения положительных рядов.
48. Признаки Даламбера и Коши сходимости рядов.
Литература
1. В.П.Григорьев, Ю.А.Дубинин «Элементы высшей математики» Москва, Академия, 2004 г.
2. С.Г.Григорьев, С.В. Задулина «Математика» Москва, Академия, 2008 г.
3. И.И. Валуце, Г.Д. Дилигул «Математика для техникумов»Москва, Наука, 2000 г.
Дополнительная литература
1. О.Н.Афанасьева, Я.С.Бродский, А.Л.Павлов «Математика для техникумов на базе среднего образования» Москва 2005 г.
2. О.Н.Афанасьева, Я.С.Бродский, И.И.Гуткин, А.Л.Павлов «Сборник задач по математике», Москва 1987 г.
3. И.Л.Соловейчик, В.Т.Лисичкин «Математика», Москва 1991г.