Рассчитаем параметры линейной модели регрессии

Для того чтобы составить уравнение регрессии зависимости индекса человеческого развития от валового накопления и ожидаемой продолжительности жизни при рождении 1997г, воспользуемся функцией программы Microsoft Excel, а именно инструмента «Регрессия».

Применение инструмента «Регрессия»

(Анализ данных EXCEL)

Для проведения регрессионного анализа необходимо выполнить следующие действия:

• Выбрать команду «Сервис»→ «Анализ данных».

• В диалоговом окне «Анализ данных» выбрать инструмент «Регрессия», а затем щёлкнуть по кнопке ОК.

• В диалоговом окне «Регрессия» в поле «Входной интервал У» ввести адрес одного диапазона ячеек, который представляет зависимую переменную. В поле «Входной интервал Х» ввести адреса одного или нескольких диапазонов, которые содержат значения независимых переменных.

• Если введены и заголовки столбцов, то следует установить флажок «Метки в первой строке».

• Выбрать параметры вывода. В данном случае «Новая рабочая книга».

• ОК

Результат произведенных действий см. Таблицу 3

Таблица 3

Регрессионная статистика
Множественный R	0,96771735
R-квадрат	0,93647687
Нормированный R-квадрат	0,93070204
Стандартная ошибка	0,02666578
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,23062	0,115309821	162,1652797	6,8E-14
Остаток		0,015643	0,000711064
Итого		0,246263
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-0,5342489	0,10353	-5,160326191	3,57641E-05	-0,74896	-0,31954
х4	-0,0020694	0,001062	-1,949082867	0,064149279	-0,00427	0,000132
х6	0,01920023	0,001234	15,56127294	2,34036E-13	0,016641	0,021759

Для того чтобы составить уравнение регрессии по нашим данным, проанализируем полученные итоги. Найдем графу «Коэффициенты» в Таблице 3.

У= -0,53425-0,00207х₄+0,019200х₆

Вывод: при увеличении валового накопления на 1% при той же ожидаемой продолжительности жизни при рождении в 1997г. индекс человеческого развития уменьшится в среднем на 0,00207. А при увеличении ожидаемой продолжительности жизни при рождении в 1997г. на 1 год при том же валовом накоплении индекс человеческого развития увеличится в среднем на 0,019200.

Оценка качества всего уравнения регрессии

В таблице № 3 приведены вычисленные (предсказанные) по модели значения зависимой переменной У и значения остаточной компоненты . Значение коэффициентов детерминации и множественной корреляции можно найти по таблице Регрессионная статистика.

Коэффициент множественной корреляции: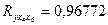

Он показывает, что связь между переменной У и объясняющими переменными х₄ и х₆ является сильной.

Коэффициент детерминации: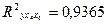

Он показывает долю вариации результативного признака под воздействием изучаемых факторов. В нашем случае 93,65 % вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.