Частные случаи общего уравнения плоскости
Лемма 1 (о параллельности вектора и плоскости). Пусть в аффинной системе координат 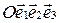 дана плоскость
дана плоскость 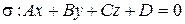 и вектор
и вектор 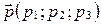 . Для того, чтобы вектор
. Для того, чтобы вектор 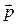 был параллелен плоскости
был параллелен плоскости 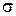 , необходимо и достаточно, чтобы выполнялось условие
, необходимо и достаточно, чтобы выполнялось условие 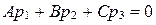 .
.
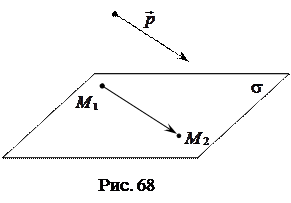
□ Чтобы доказать необходимость и достаточность этого условия, возьмем точку 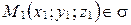 и отложим от нее вектор
и отложим от нее вектор 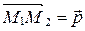 (рис. 68).
(рис. 68).
Пусть 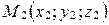 , тогда
, тогда  .
.
 Из равенства векторов
Из равенства векторов 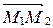 и
и 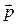 следует равенство их соответственных координат:
следует равенство их соответственных координат:
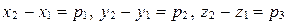 . (24)
. (24)
Так как 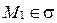 , то
, то
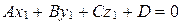 . (25)
. (25)
Если 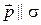 , то
, то 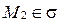 , следовательно,
, следовательно,
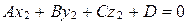 . (26)
. (26)
Вычитаем почленно из уравнения (26) уравнение (25):
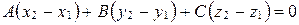 .
.
Применяя формулы (24), получаем:
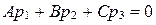 .
.
Обратно, пусть имеет место условие 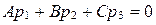 . Тогда из формул (24) следует, что
. Тогда из формул (24) следует, что 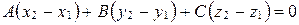 .
.
Сложив почленно последнее уравнение с уравнением (25), получим:
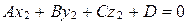 ,
,
откуда следует, что 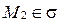 . Поэтому
. Поэтому 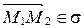 , а так как
, а так как 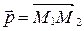 , то
, то 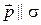 . ■
. ■
Выясним особенности расположения плоскости 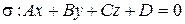 относительно аффинной системы координат, если некоторые из коэффициентов в ее общем уравнении равны 0.
относительно аффинной системы координат, если некоторые из коэффициентов в ее общем уравнении равны 0.
1. 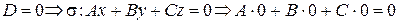 - верное равенство
- верное равенство 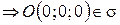 .
.
Обратно, пусть 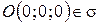 , тогда
, тогда 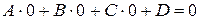 - верное равенство
- верное равенство 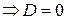 .
.
Итак, 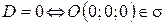 .
.
2. 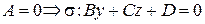 .
.
Возьмем вектор 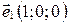 . Проверим выполнимость условия
. Проверим выполнимость условия 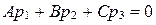 :
:
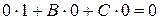 ;
;
0=0.
Следовательно, по лемме о параллельности вектора и плоскости 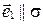 . Поэтому возможны два случая
. Поэтому возможны два случая 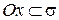 или
или 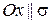 . Учитывая, что
. Учитывая, что 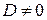 , т.е.
, т.е. 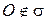 , получаем:
, получаем: 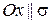 .
.
Обратно, пусть 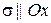 , тогда
, тогда 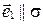 . По лемме о параллельности вектора и плоскости
. По лемме о параллельности вектора и плоскости 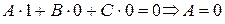 .
.
Итак, 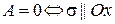 .
.
Рассуждая аналогично, рассмотрите самостоятельно случаи 3 и 4 :
3. 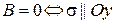 .
.
4. 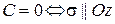 .
.
5. Пусть 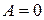 и
и 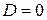 . Тогда из пункта 2 следует, что
. Тогда из пункта 2 следует, что 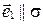 , т.е.
, т.е. 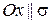 или
или 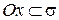 ; а из пункта 1 следует, что
; а из пункта 1 следует, что 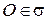 . Значит,
. Значит, 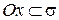 .
.
Обратно, пусть 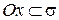 . Тогда
. Тогда 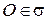 , т.е.
, т.е. 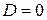 (см. пункт 1). Кроме того,
(см. пункт 1). Кроме того, 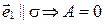 (см. пункт 2).
(см. пункт 2).
Итак, 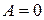 и
и 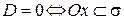 .
.
В этом случае уравнение плоскости 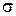 примет вид
примет вид 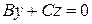 .
.
Рассуждая аналогично, рассмотрите самостоятельно случаи 6 и 7:
6. 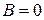 и
и 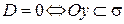 .
.
7. 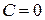 и
и 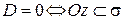 .
.
8. 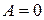 и
и 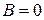 . Тогда из пункта 2 следует, что
. Тогда из пункта 2 следует, что 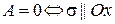 ; а из пункта 3 следует, что
; а из пункта 3 следует, что 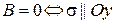 . Таким образом,
. Таким образом,
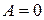 и
и 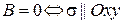 .
.
В этом случае уравнение 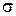 примет вид
примет вид 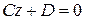 или
или 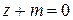 (где
(где 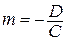 ).
).
Рассуждая аналогично, рассмотрите случаи 9 и 10:
9. 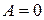 и
и 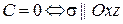 .
.
10. 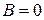 и
и 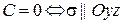 .
.
Из пунктов 8 и 1 получаем случай
11. 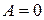 ,
, 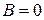 и
и 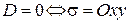 .
.
В этом случае уравнение плоскости будет иметь вид 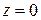 , т.е.
, т.е.
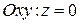 .
.
Из пунктов 9 и 1 получаем случай
12. 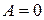 ,
, 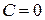 и
и 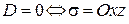 .
.
Тогда уравнение 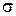 будет иметь вид
будет иметь вид 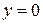 , т.е.
, т.е.
 .
.
Из пунктов 10 и 1 получаем случай
13. 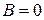 ,
, 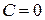 и
и 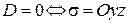 .
.
Уравнение 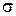 в этом случае имеет вид
в этом случае имеет вид 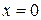 , т.е.
, т.е.
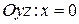 .
.
Задания для самостоятельной работы
1. Какие из векторов 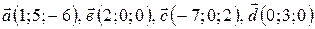 параллельны плоскости
параллельны плоскости 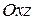 и почему?
и почему?
2. Справедливы ли утверждения, доказанные в пунктах 1-13, если уравнение плоскости задано в прямоугольной декартовой системе координат и почему?
3. Составьте уравнение плоскости, проходящей через точку 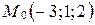 и параллельной плоскости: а)
и параллельной плоскости: а) 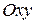 ; б)
; б) 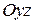 ; в)
; в) 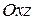 (пользуясь частными случаями общего уравнения плоскости).
(пользуясь частными случаями общего уравнения плоскости).
4. Составьте уравнение плоскости, которая проходит через точку 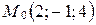 и содержит: а) ось
и содержит: а) ось 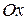 ; б) ось
; б) ось 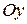 ; в) ось
; в) ось 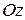 (пользуясь частными случаями общего уравнения плоскости).
(пользуясь частными случаями общего уравнения плоскости).
Основные аффинные задачи,
