Основные сведения из теории

Определение 1.Графиком функции 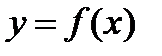называется совокупность всех точек плоскости, абсциссы которых есть значения аргумента, взятые из области существования функции, а ординаты, соответствующие этим значениям аргумента,—значения функции.

Согласно этому определению, для построения точного графика функции нам следовало бы построить все точки, принадлежащее графику, а это, как правило, сделать невозможно так как, вообще говоря, график функции содержит бесконечное множество точек.

Для построения графика функции 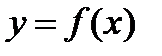обычно поступают так: дают аргументу насколько частных значений и пользуясь аналитическим выражением функции, вычисляют соответствующие значения функции. Если, например, взяты значения аргумента 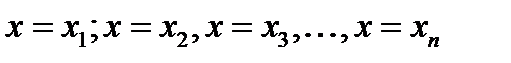, то соответствующими им значениями функции будут .

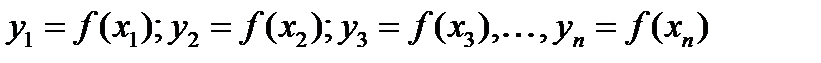Эти значения сводят в таблицу такого вида:

х	у

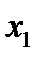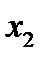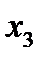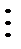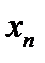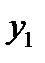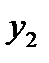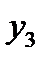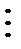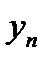После этого берут прямоугольную систему координат, выбирают масштабную единицу и строят, выбирают масштабную единицу и строят точки .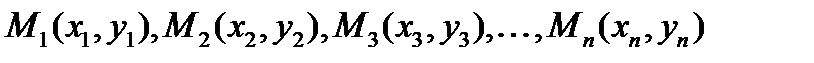

Полученные точки соединяют плавной кривой. Эта кривая дает эскиз графика функции (приближенный график). Прежде чем приступить к составлению таблицы числовых значений функции, очень полезно выяснить вопрос и симметрии графика функции.

Если функцию можно отнести к классу четных или нечетных функций, то построение е графика значительно облегчится. Приведем относящиеся сюда определения.

Определение 2.Область существования функции называется симметричной, если вместе с числом 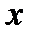этой области принадлежит число— 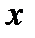(на геометрическом языке это значит, что симметрическая область существования функции расположена симметрично относительно начала координат).

Определение3. Функция 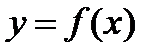называется четной на симметричной относительно начала координат области, если для каждого значения аргумента 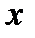из этой области имеет место равенство

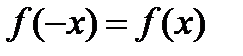
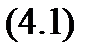
Таким образом, если функция – четная, то изменение знака у аргумента не имеет значения функции, а поэтому в случае четной функции каждой точке ее графика с абсциссой 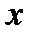и ординатой 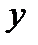соответствует точка, имеющая абсциссу— 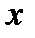и ту же ординату .

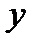Это приводит к выводу, что график четной функции расположен симметрично относительно оси .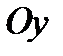

Таким образом, если функция четная, то ее график мы будем строить так:

1) Построим только часть графика этой функции, расположенную справа от оси 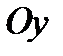,т.е. при составлении таблицы числовых значений функции будем давать аргументу только положительные значения и значение, равные нулю, если это значение принадлежит области существования функции.

2) Построим «зеркально отражение» относительно оси 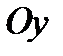графика, полученного п. 1).

Определени43. Функция 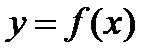называется нечетной на симметричной относительно начала координат области, если для каждого значения аргумента 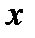из этой области имеет место равенство

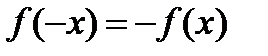
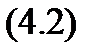
Таким образом, у нечетной функции изменение на противоположный знака аргумента изменяет на противоположный и знак функции, не изменяя ее абсолютной величины.

Поэтому график нечетной функции расположен симметрично относительно начала координат, так как если графику принадлежит точка 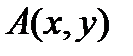, то ему же принадлежит и точка , .

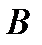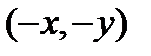Для построения графика нечетной функции надо: 1) Построить только ту часть графика, которая расположена справа от оси 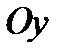, т.е. часть, соответствующую положительным значениям аргумента (и значению 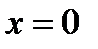, если нуль принадлежит области существования функции); 2) построить кривую, симметричную относительно начала координат кривой постоянной а п. 1).

Эти свойства четных и нечетных функций будут использованы при построении графиков функций.

Задачи 4.1 – 4.12 являются упражнениями, связанными с определениями четной и нечетной функций.