Рациональные дроби. Интегрирование простейших рациональных функций
Определение
Многочленом степени n называется выражение вида
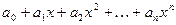 , , | (7.6.А) |
где 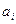 – действительные числа,
– действительные числа, 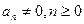 .
.
Определение
Рациональной дробью (рациональной функцией) называется отношение двух многочленов 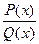 .
.
Определение
Если степень многочлена числителя не меньше степени многочлена знаменателя, то такая дробь называется неправильной. Если меньше, то дробь правильная.
Пусть 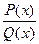 – неправильная дробь, тогда, выполнив деление, получаем
– неправильная дробь, тогда, выполнив деление, получаем
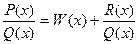 , , | (7.6.Б) |
где 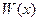 – некоторый многочлен, а
– некоторый многочлен, а 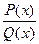 – правильная дробь.
– правильная дробь.
Пример
1. 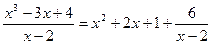 .
.
2. 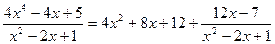 .
.
3. 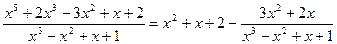 .
.
Из высшей алгебры известно, что любой многочлен с вещественными коэффициентами может быть единственным образом представлен в виде произведения, содержащего множители вида 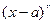 и
и 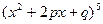 , причем квадратные сомножители не имеют вещественных корней.
, причем квадратные сомножители не имеют вещественных корней.
Таким образом, если 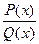 – правильная рациональная дробь, у которой знаменатель представлен в виде многочлена, тогда эту дробь можно представить в виде суммы простых дробей:
– правильная рациональная дробь, у которой знаменатель представлен в виде многочлена, тогда эту дробь можно представить в виде суммы простых дробей:
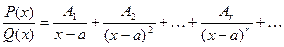 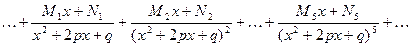 . . | (7.6.В) |
В формуле (7.0.В) 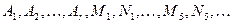 – некоторые вещественные числа.
– некоторые вещественные числа.
Выражение (7.6.В) называется разложением рациональной дроби на простые дроби.
Чтобы определить неизвестные коэффициенты 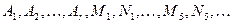 , умножим обе части выражения (7.6.В) на
, умножим обе части выражения (7.6.В) на 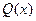 . Так как равенство между многочленом
. Так как равенство между многочленом  в левой чисти и многочленом в правой части должно соблюдаться для всех
в левой чисти и многочленом в правой части должно соблюдаться для всех 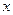 , то коэффициенты при одинаковых степенях
, то коэффициенты при одинаковых степенях 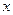 в обеих частях должны быть равны между собой. Приравнивая их получим систему линейных алгебраических уравнений относительно чисел из формулы (7.6.В). Этот метод нахождения коэффициентов разложения (7.6.В) правильной рациональной дроби на сумму простых дробей называется методом неопределенных коэффициентов.
в обеих частях должны быть равны между собой. Приравнивая их получим систему линейных алгебраических уравнений относительно чисел из формулы (7.6.В). Этот метод нахождения коэффициентов разложения (7.6.В) правильной рациональной дроби на сумму простых дробей называется методом неопределенных коэффициентов.
Рассмотрим применение этого метода на примерах.
1. 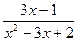 .
.
Знаменатель имеет два корня 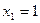 и
и 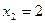 . Разложение этой дроби на простые имеет вид
. Разложение этой дроби на простые имеет вид 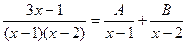 . Умножая обе части этого равенства на
. Умножая обе части этого равенства на 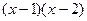 , получаем
, получаем 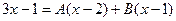 . Приравнивая коэффициенты при одинаковых степенях
. Приравнивая коэффициенты при одинаковых степенях 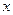 в обеих частях последнего равенства, получаем систему двух линейных уравнений относительно A и B.
в обеих частях последнего равенства, получаем систему двух линейных уравнений относительно A и B.
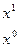
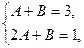 откуда
откуда 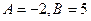 .
.
Подставляя эти числа, получаем искомое разложение
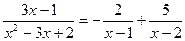 .
.
2. 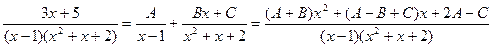 .
.
A = 2, B = –2, C = –1.
Окончательно, 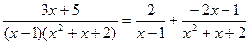 .
.
Интегрирование простейших рациональных функций
Выделим из класса правильных дробей так называемые основные простые дроби. Это дроби следующих четырех типов:
1. 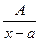 . 2. . 2. 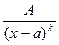 . 3. . 3. 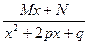 . 4. . 4. 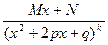 . . | (7.6.1) |
Здесь – 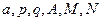 – вещественные числа,
– вещественные числа, 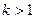 – целое число; кроме того, предполагается, что знаменатели дробей III и IV типов не имеют вещественных корней, т.е. (дискриминант мнимый)
– целое число; кроме того, предполагается, что знаменатели дробей III и IV типов не имеют вещественных корней, т.е. (дискриминант мнимый)
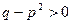 . . | (7.6.2) |
Рассмотрим интегралы от четырех основных видов простых дробей.
Дроби типов 1 и 2 интегрируются с помощью подстановки 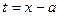 :
:
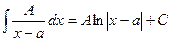 ; ; 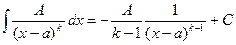 . . | (7.6.3) |
Для интегрирования дробей типа 3 выделим из трехчлена в знаменателе полный квадрат 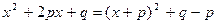 .
.
Отсюда следует подстановка 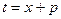 ,
, 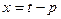 ,
, 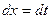 , и тогда
, и тогда
 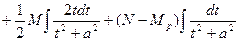 | (7.6.4) |
где 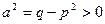 по условию (7.6.2). Первый интеграл в правой части берется непосредственно, а второй интеграл с помощью подстановки
по условию (7.6.2). Первый интеграл в правой части берется непосредственно, а второй интеграл с помощью подстановки 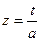 сводится к табличному:
сводится к табличному:
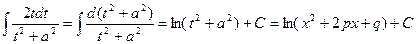 , , | (7.6.4а) |
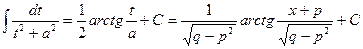 . . | (7.6.4б) |
Таким образом, окончательно получаем
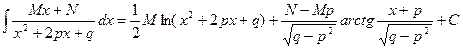 | (7.6.5) |
Пример
Вычислить интеграл 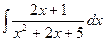 .
.
Решение
Осуществим следующие подстановки: 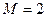 ,
, 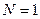 ,
, 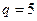 ,
, 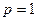 . Получаем
. Получаем
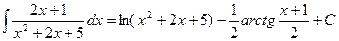 .
.
Теперь найдем интеграл от дроби 4. Введем новую переменную 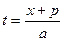 , где
, где 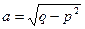 , откуда
, откуда 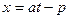 ,
, 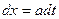 . В результате подстановки получаем
. В результате подстановки получаем
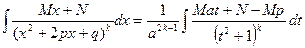 | (7.6.6) |
Разобьем интеграл в правой части последнего выражения на два слагаемых
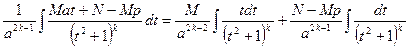 | (7.6.7) |
Первый интеграл сводится к табличному подстановкой 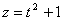 :
:
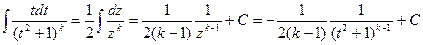 | (7.6.8) |
Из изложенного выше следует, что при интегрировании правильных дробей необходимо сначала выполнить разложение (7.6.В) и методом неопределенных коэффициентов найти коэффициенты разложения. Таким образом, в разложении (7.6.В) получается сумма четырех видов основных дробей, интегралы от которых подробно рассмотрены ранее.
Вывод
Всякая рациональная дробь интегрируется в элементарных функциях.
