Интегрирование рациональных функций.

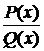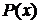Рациональной называется функция, представимая в виде дроби , где и 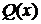-- многочлены. Рациональная дробь называется правильной если степень многочлена, стоящего в числителе, меньше степени многочлена в знаменателе. В противном случае рациональная дробь называется неправильной. Рассмотрим сначала два частных случая интегрирования правильной рациональной дроби, когда в знаменателе стоит многочлен второй степени.

1) 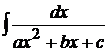. В этом случае нужно в знаменателе выделить полный квадрат.

Пример 1.21. Вычислить .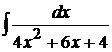

Выделим в знаменателе квадрат суммы, получим

.

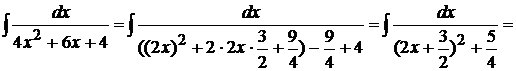
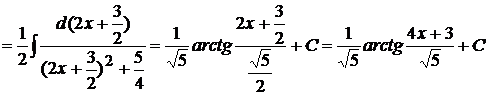2) 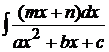. Чтобы вычислить такого типа интеграл, нужно в числителе выделить производную знаменателя.

Пример 1.22. Вычислить .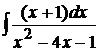

Найдем производную знаменателя: 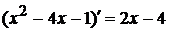. Для того, чтобы выделить такое же выражение в числителе, умножим и разделим числитель на 2. Получим

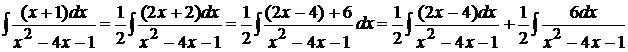В первом интеграле многочлен, стоящий в числителе внесем под знак дифференциала, а второй интеграл после вынесения постоянного множителя 6 за интеграл, станет интегралом первого типа, рассмотренного выше. Тогда

.

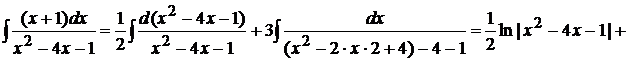
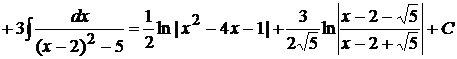Если знаменатель 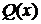правильной рациональной дроби степени выше, чем вторая, то он может быть представлен в виде

,

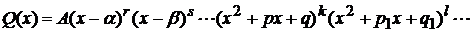где А – коэффициент при старшей степени многочлена 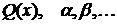-- корни уравнения 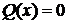, а трехчлены не имеют действительных корней. Тогда эта дробь разлагается на сумму элементарных дробей следующим образом:

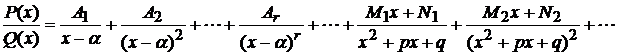
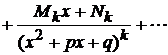(1.4),

где 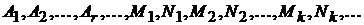-- некоторые неизвестные числа (коэффициенты). Для их определения умножаем обе части последнего равенства на 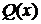. Получаем равенство двух многочленов. Далее, приравнивая между собой коэффициенты при одинаковых степенях в левой и правой частях, получим систему линейных уравнений, из которой найдем неизвестные числа.

Заметим, что после умножения на 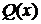, в случае, когда 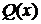имеет действительные корни, целесообразно подставить в обе части получившегося равенства последовательно эти корни. В результате найдем часть неизвестных чисел. Изложенный метод отыскания разложения рациональной функции называется методом неопределенных коэффициентов.

Если рациональная дробь неправильная, то всегда с помощью деления многочле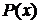на на 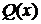можем представить 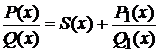, где 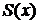--многочлен, а 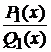--- правильная рациональная дробь.

Пример 1.23. Вычислить .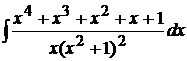

Подынтегральная функция – правильная рациональная дробь. Так как 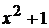не имеет действительных корней, то по формуле (1.4) имеем

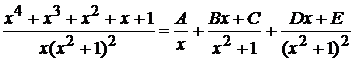, где 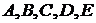--- неизвестные коэффициенты. Умножая обе части равенства на 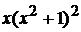, получаем

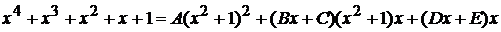, или

.

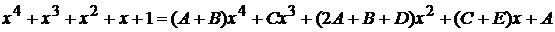Приравнивая коэффициенты при одинаковых степенях 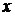, придем к системе уравнений

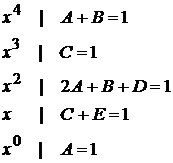
Решая эту систему, найдем 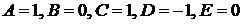. Искомое разложение имеет вид: 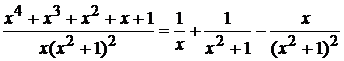. Следовательно,

.

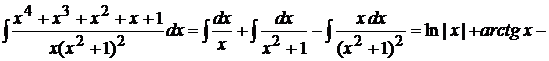
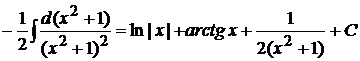Пример 1.24. Вычислить .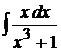

Подынтегральная функция – правильная рациональная дробь. Так как 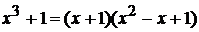, причем второй сомножитель не имеет действительных корней, то по формуле (1.4) имеем 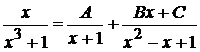, где 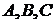-- неизвестные коэффициенты. Умножая обе части равенства на 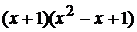, получаем .

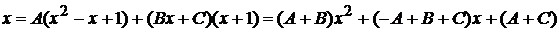Приравнивая коэффициенты при одинаковых степенях 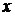и решая систему уравнений, получим 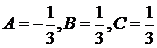. Таким образом,

.

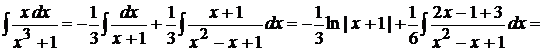
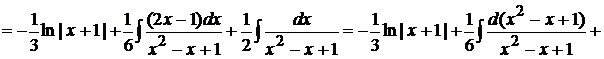
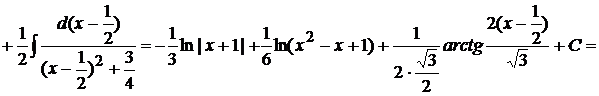
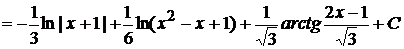Обратите внимание, последний интеграл в этом соотношении оказался интегралом первого типа из рассматриваемых нами выше, поэтому для его вычисления мы в квадратном трехчлене 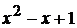выделили полный квадрат.

Пример 1.25. Вычислить .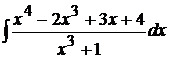

Подынтегральная функция --- неправильная рациональная дробь, поэтому выделим ее целую часть делением числителя на знаменатель. В результате получим: 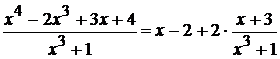. Полученную справа правильную дробь разложим на простые дроби. .

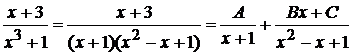Отсюда 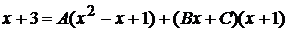. Полагая 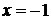, находим 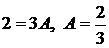. Сравнивая коэффициенты при одинаковых степенях 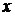, получим

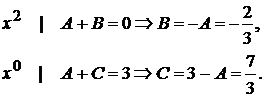
Следовательно, 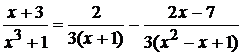. Далее, находим

.

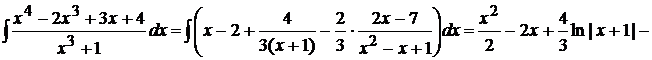
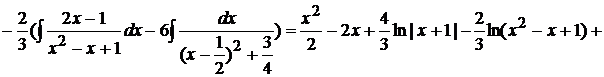
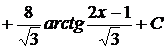Пример 1.26. Вычислить .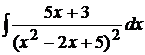

В числителе подынтегральной функции выделим производную квадратного трехчлена, стоящего в знаменателе .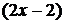

.

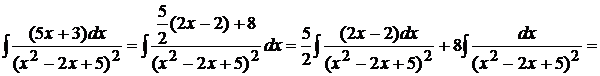
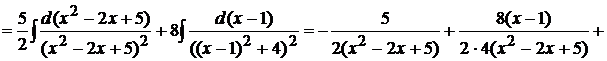
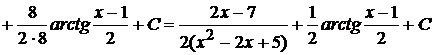При вычислении последнего интеграла мы воспользовались формулой (1.3).

Упражнения.

1.4. Вычислить интегралы (в скобках указаны ответы).

1). ;

2). ;

3). ;

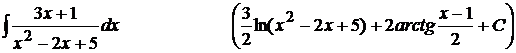4). ;

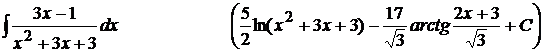5). ;

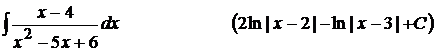6). ;

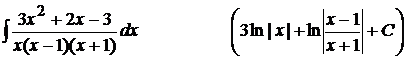7). ;

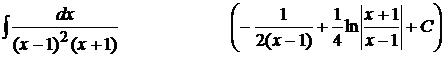8). ;

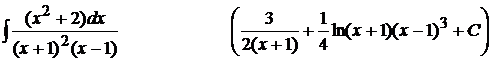9). ;

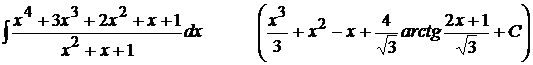10). ;

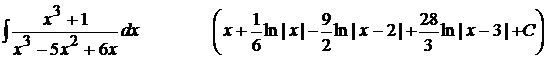11). ;

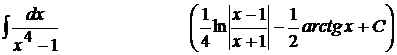12). ;

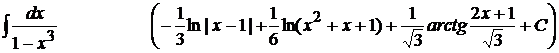13). ;

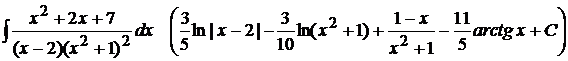14). ;

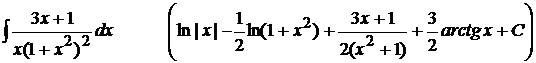15). .

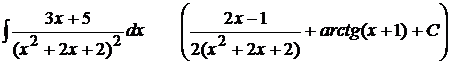1.5. Нахождение интегралов вида .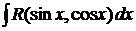

Отметим, что R обозначает рациональную функцию своих аргументов 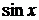и 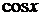. Эти интегралы сводятся к интегралам от рациональной функции с помощью так называемой универсальной подстановки .

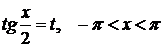Так как 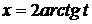, то . .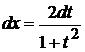

.

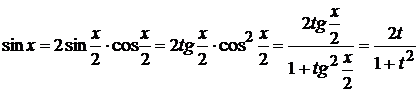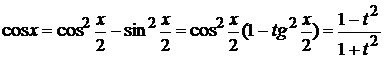Пример 1.27. Вычислить

.

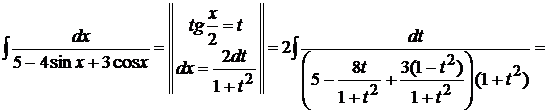
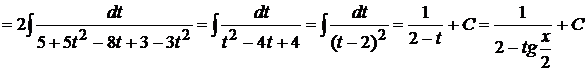Однако на практике универсальная подстановка часто приводит к слишком сложным и трудоемким выкладкам, поэтому наряду с универсальной подстановкой полезно знать и другие постановки, которые во многих случаях быстрее приводят к цели.

Если функция 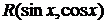нечетна относительно 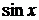, то есть 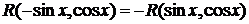, то рационализация интеграла достигается с помощью подстановки .

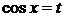Если функция 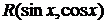нечетна относительно 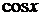, то используется подстановка .

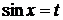Если функция 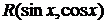четна относительно 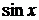и 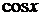, то есть 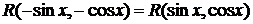, то целесообразна подстановка .

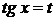Пример 1.28. Вычислить

.

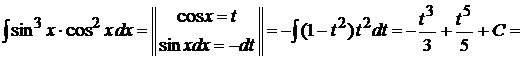
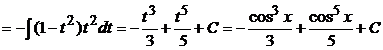Пример 1.29. Вычислить

.

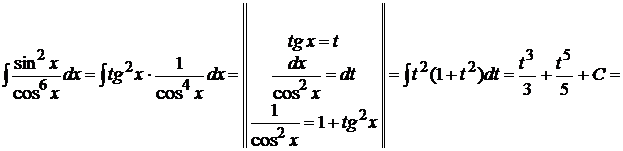
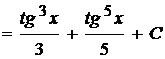Иногда при вычислении интегралов указанного вида бывает полезно прибегать и к другим искусственным приемам, используя известные тригонометрические формулы, как, например, формулу .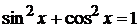

Пример 1.30. Вычислить

.

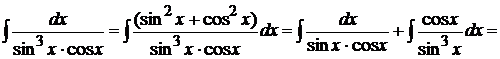
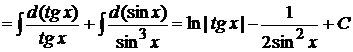Замечание 1. Если в интеграле вида 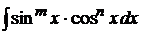оба показателя степени m и n положительны и четны, то целесообразно применять формулы

,

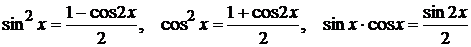которые приводят данный интеграл к интегралу с меньшими неотрицательными показателями.

Замечание 2. Интегралы вида 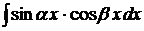непосредственно вычисляются с помощью формул: ,

,

.

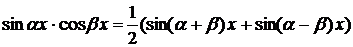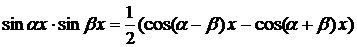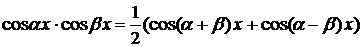Пример 1.31. Вычислить

.

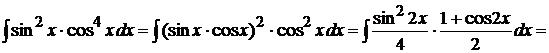
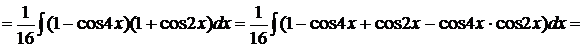
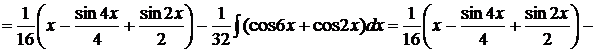
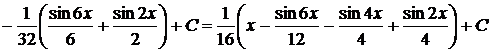Упражнения.

1.5. Вычислить интегралы (в скобках указаны ответы).

1). ;

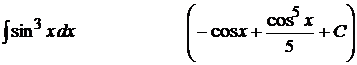2). ;

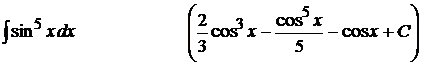3). ;

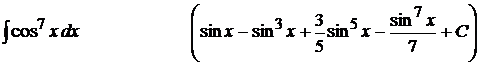4). ;

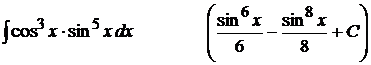5). ;

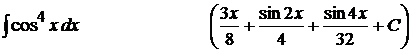6). ;

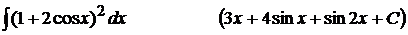7). ;

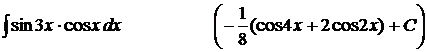8). ;

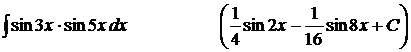9). ;

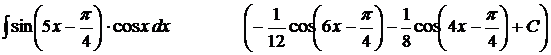10). ;

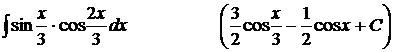11). ;

12). ;

13). ;

14). ;

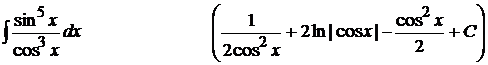15). ;

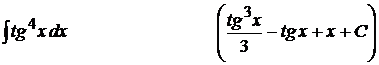16). ;

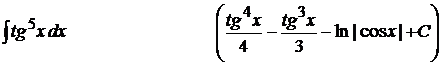17). ;

18). ;

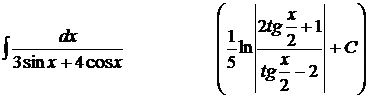19). ;

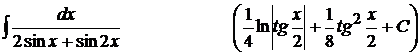20). ;

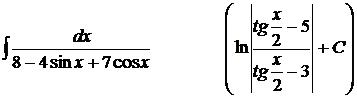21). ;

22). ;

23). .

Определенный интеграл

2.1. Определение определенного интеграла. Пусть функция 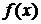определена на отрезке 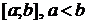. Разобьем отрезок на 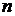произвольных частей точками 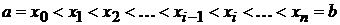. В каждом из полученных частичных отрезков 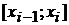выберем произвольную точку 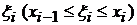и составим сумму 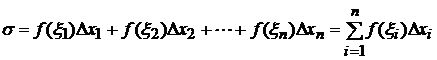, где 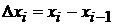. Эта сумма называется интегральной суммой для функции 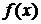на 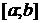. Обозначим через 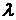длину наибольшего частичного отрезка разбиения: .

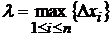Определение 2.1. Если существует конечный предел 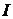интегральной суммы при 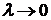и он не зависит от выбора точек 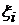, то этот предел называется определенным интегралом от функции 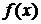по отрезку 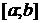и обозначается следующим образом:

.

В этом случае функция 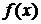называется интегрируемой на 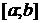. Числа 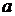и 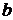называются соответственно нижним и верхним пределами интегрирования, 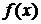-- подынтегральной функцией, 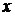--переменной интегрирования.

Для интегрируемости функции достаточно ее непрерывности на 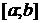. В дальнейшем будем предполагать, что рассматриваемые функции непрерывны на .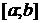