Интегрирование рациональных функций (181-190, г)
Отношение двух многочленов называется рациональной функцией. Если степень многочлена в числителе меньше степени многочлена в знаменателе, то рациональная функция называется правильной, в противном случае – неправильной. Простейшими рациональными функциями называются функции вида
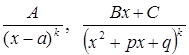 ,
,
где 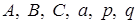 – действительные числа;
– действительные числа; 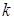 – натуральное число и
– натуральное число и 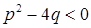 .
.
Алгоритм интегрирования рациональной функции:
1. Если рациональная функция неправильная, то с помощью деления ее нужно представить в виде суммы многочлена и правильной рациональной функции.
2. Знаменатель правильной рациональной функции нужно разложить на линейные и квадратичные множители.
3. Используя метод неопределенных коэффициентов, разложить правильную рациональную функцию на сумму простейших.
4. Проинтегрировать все полученные слагаемые.
Пример.Вычислить 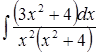 .
.
Подынтегральная функция правильная, и ее знаменатель разложен на множители, поэтому переходим к третьему пункту алгоритма. Разложение на сумму простейших для этой функции будет иметь вид
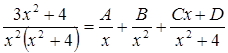 ,
,
где 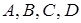 – некоторые числа (неопределенные коэффициенты), которые нужно найти. Дроби в правой части приводим к общему знаменателю (он равен
– некоторые числа (неопределенные коэффициенты), которые нужно найти. Дроби в правой части приводим к общему знаменателю (он равен 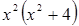 ) и приравниваем числители.
) и приравниваем числители.
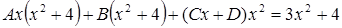 .
.
Приравнивая коэффициенты при одинаковых степенях 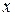 в левой и правой части, получим систему уравнений.
в левой и правой части, получим систему уравнений.
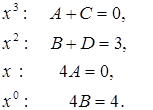
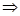
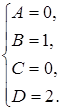
Таким образом,
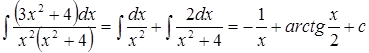 .
.
1912200.Если 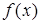 – непрерывная функция на
– непрерывная функция на 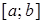 и
и 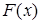 – первообразная для
– первообразная для 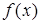 , то определенный интеграл
, то определенный интеграл 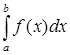 можно вычислить по формуле Ньютона-Лейбница
можно вычислить по формуле Ньютона-Лейбница
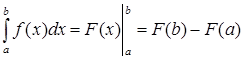 .
.
Пример.
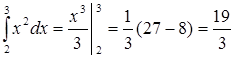 .
.
При вычислении определенного интеграла можно использовать формулу интегрирования по частям:
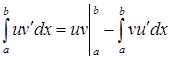 .
.
(функции 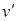 и
и 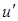 должны быть непрерывны на
должны быть непрерывны на 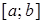 ).
).
Пример.
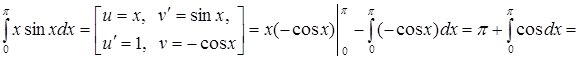
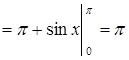 .
.
В определенном интеграле можно сделать замену переменной 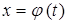 , тогда
, тогда
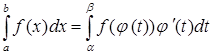 ,
,
где числа 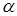 и
и 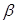 такие, что
такие, что 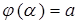 ,
, 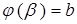 (функция
(функция 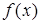 должна быть непрерывна на
должна быть непрерывна на 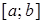 , функция
, функция 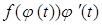 – непрерывна на
– непрерывна на 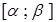 ).
).
201 − 210.
Геометрические приложения определенного интеграла .
Пусть функция 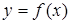 непрерывна и неотрицательна на
непрерывна и неотрицательна на 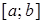 . Тогда площадь
. Тогда площадь 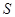 криволинейной трапеции
криволинейной трапеции 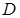 (рис.5), ограниченной графиком функции
(рис.5), ограниченной графиком функции 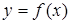 , осью
, осью 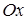 и прямыми
и прямыми 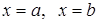 вычисляется по формуле
вычисляется по формуле
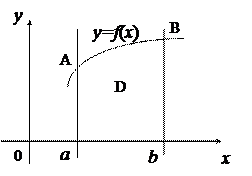
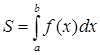 .
.
|
Рис. 5
Длина дуги 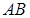 , заданной графиком функции
, заданной графиком функции 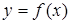 , вычисляется по формуле
, вычисляется по формуле
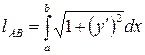 .
.
Если функция 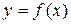 задана параметрически уравнениями
задана параметрически уравнениями 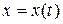 ,
, 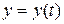 , где
, где 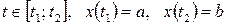 , то
, то
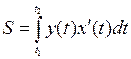 ,
, 
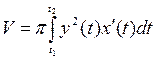 ,
,
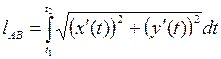 .
.
Пусть в полярной системе координат задана функция 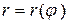 , где
, где 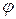 – полярный угол,
– полярный угол, 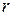 – полярный радиус точки.
– полярный радиус точки.
| |||
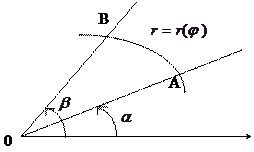 | |||
Рис. 6
Длина дуги вычисляется по формуле 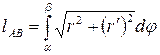 .
.
Пример.Вычислить длину одной арки циклоиды 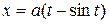 ,
, 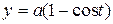 ,
, 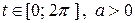 .
.
Решение. Нарисуем арку циклоиды (рис. 7). Заметим, что если 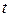 меняется от 0 до
меняется от 0 до 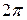 , то
, то 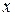 возрастает от 0 до
возрастает от 0 до 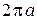 , а
, а 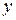 сначала возрастает от 0 до
сначала возрастает от 0 до 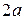 , а затем убывает до 0.
, а затем убывает до 0.
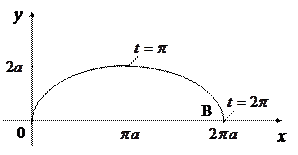 | |||||||
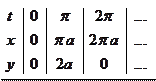 | |||||||
 | |||||||
 |
Рис. 7
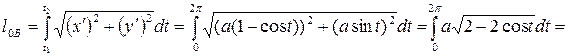
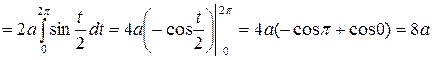 .
.
211 − 220.Несобственные интегралы – это обобщение понятия определенного интеграла для случая, когда либо неограниченным является промежуток интегрирования, либо неограничена подынтегральная функция на отрезке интегрирования. Рассмотрим эти два случая.
1. Пусть функция 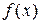 непрерывна на
непрерывна на 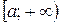 , тогда
, тогда 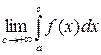 называется несобственным интегралом от функции
называется несобственным интегралом от функции 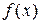 на промежутке
на промежутке 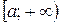 и обозначается
и обозначается 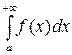 , т.е.
, т.е.
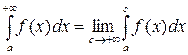 ,
,
при этом, если существует конечный предел, говорят, что несобственный интеграл сходится, в противном случае – расходится.
Аналогично
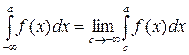 ,
,
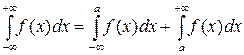 , ( 1 )
, ( 1 )
при этом несобственный интеграл в левой части формулы (1) называется сходящимся, если оба несобственных интеграла в правой части формулы (1) сходятся (число а в формуле (1) можно выбрать произвольно).
2. Пусть функция 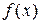 непрерывна на
непрерывна на 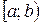 и
и 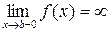 , тогда
, тогда 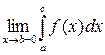 называется несобственным интегралом и обозначается
называется несобственным интегралом и обозначается 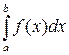 , т.е.
, т.е.
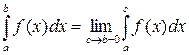 ,
,
при этом, если существует конечный предел, то несобственный интеграл называется сходящимся.
Возможны другие случаи, например,
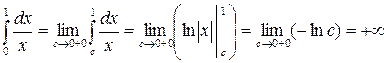 .
.
Следовательно, несобственный интеграл 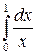 расходится.
расходится.

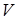 тела, образованного вращением криволинейной трапеции
тела, образованного вращением криволинейной трапеции 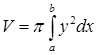 .
. 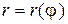 непрерывна на
непрерывна на 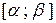 , то площадь криволинейного сектора
, то площадь криволинейного сектора 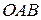 , ограниченного графиком функции
, ограниченного графиком функции 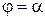 ,
, 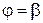 (рис. 6), вычисляется по формуле:
(рис. 6), вычисляется по формуле: 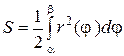 .
.