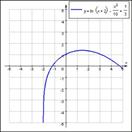
Физический смысл производной

Свойства функции arcsin

§ (функция является нечётной).

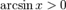§ при .

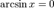§ при x = 0.

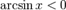§ при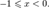

§

§

§

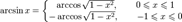
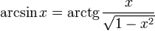
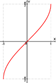
График функции y = arccos x

.

Арккосинусом числа m называется такое значение угла x, для которого

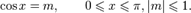
Функция y = cos x непрерывна и на всей своей числовой прямой.

Функция y = arccos x является строго убывающей.

§ cos(arccos x) = x при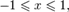

§ arccos(cos y) = y при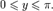

§ D(arccos x) = [ − 1;1], (область определения),

§ E(arccos x) = [0;π]. (область значений).

Свойства функции arccos

§

§

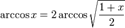
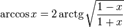
§ при

§ при

§

§

§

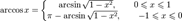
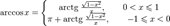
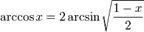
Арктангенсом числа m называется такое значение угла α,

для которого

Функция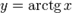

непрерывна и ограничена на всей своей числовой прямой.

Функция 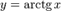является строго возрастающей.

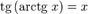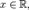
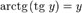при

при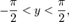

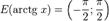
Свойства функции arctg

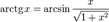
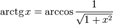
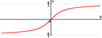
Арккотангенсом числа m называется такое значение угла x,

для которого

Функция 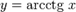непрерывна и ограничена на всей

своей числовой прямой. Функция 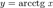является строго убывающей.

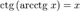§ при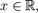

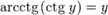§ при 0 < y < π,

§

§

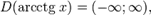
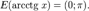
Свойства функции arcctg

§

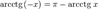
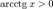§ при любых x.

§

§

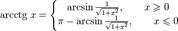
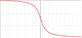
cos x = 1, x = 2n; n 2 Z sin x = 1. x =/2+ 2n; n 2 Z tg x = 1. x =/4+ n; n 2 Z

cos x = -1, x = + 2n; n 2 Z: Sinx=-1, x = /2+ 2n; n 2 Z tg x =- 1. x = 4+ n; n 2 Z:

cos x = 0. x =/2+ n; n 2 Z Sinx=-0, x = n; n 2 Z: tg x = 0. x = n; n 2 Z:

2. Уравнения, сводящиеся к квадратным.

sin ² x – cosx –1 = 0.

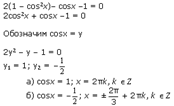
3. Однородные уравнения

1) Решить уравнение 2sinx – 3cosx = 0

Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin ² x + cos ² x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим

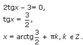
Уравнения, сводящиеся к простейшим.

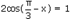
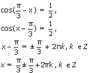
Произво́дная — основное понятие дифференциального исчисления,

характеризующее скорость изменения функции

1. (u^m)' = m u^m-1 u' (m принадлежит R¹ )

2. (a^u)' = a^u lna× u'.

3. (e^u)' = e^u u'.

4. (log_a u)' = u'/(u ln a).

5. (ln u)' = u'/u.

6. (sin u)' = cos u× u'.

7. (cos u)' = - sin u× u'.

8. (tg u)' = 1/ cos²u× u'.

9. (ctg u)' = - u' / sin²u

.

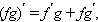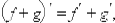
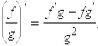
Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке

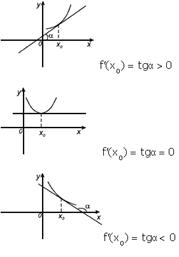
Уравнение касательной к графику функции y=f(x) в точке x₀ :

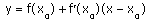
Физический смысл производной.

Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:

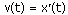
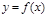называется возрастающей (неубывающей)

на интервале 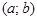если для любых 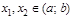таких, что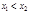

значения функци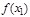и и 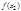удовлетворяют

неравенству 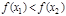[1] ( ).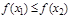

Функция 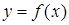называется убывающей (невозрастающей)

на интервале 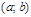если для любых 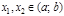таких,

что 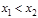значения функци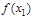и и 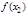удовлетворяют неравенству

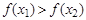[2] ( ).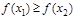

Интервалы возрастания и убывания функции называются

интервалами монотонности функции.

Наибольшим значением функции на отрезке называется самое

большое из всех ее значений на этом отрезке, анаименьшим –

самое маленькое из всех ее значений.

Найти наибольшее и наименьшее значения функции

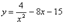на отрезке [–2; –0,5].

Найдем критические точки функции

.

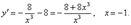
Вычислим значения функции в найденной точке и на концах

заданного отрезка.

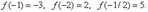
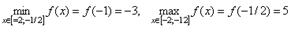
Аси́мпто́та^[1] (от греч. ασϋμπτωτος — несовпадающий, не касающийся)

кривой с бесконечной ветвью — прямая, обладающая тем свойством,

что расстояние от точки кривой до этой прямой стремится к нулю

при удалении точки вдоль ветви в бесконечность^[2]

Вертикальная

Вертикальная асимптота — прямая вида

при условии существования предела .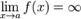



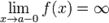
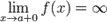
Горизонтальная

Горизонтальная асимптота — прямая вида

при условии существования предела

.

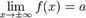Наклонная

Наклонная асимптота — прямая вида

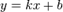при условии существования пределов

Пример наклонной асимптоты

1.

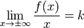
2.

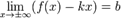
П. Исследование графика функции по первой производной:

1) найти решение уравнений y’(х)=0 и y’(х)=¥ ;

2) точки, “подозрительные” на экстремум,