Определение точек, «подозрительных на перегиб». Достаточное условие точки перегиба

достаточные условия того, что данная точка кривой является точкой перегиба.

Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x₀) = 0 или f ''(x₀) не существует и при переходе через значение x = x₀производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x₀ есть точка перегиба.

Не все точки x, в которых y′′=f′′(x)=0 или y′′=f′′(x) не существует, непременно должны быть точками перегиба. Точками перегиба будут лишь те из них, в которых вторая производная y′′=f′′(x) меняет знак (с (+) на (–) или с (–) на (+)). Таким образом, точки оси ох, в которых y′′=f′′(x)=0 или y′′=f′′(x) не существует, являются лишь подозрительными на перегиб.

Определение асимптоты графика функции. Виды асимптот. Уравнения асимптот

Асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.

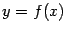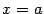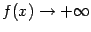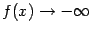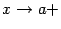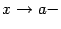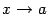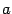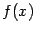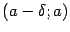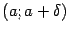Определение 7.1 Вертикальной асимптотой графика функции называется вертикальная прямая , если или при каком-либо из условий: , , . Заметим, что мы при этом не требуем, чтобы точка принадлежала области определения функции , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: или , где .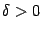

Определение 7.2 Наклонной асимптотой графика функци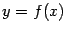и при 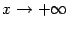называется прямая 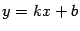, если выполнены два условия:
1) некоторый луч 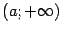целиком содержится в ;
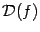2) расстояние по вертикали между графиком и прямой стремится к 0 при :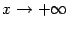

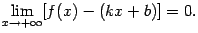Уравнения асимптот: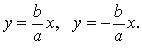

Определение первообразной. Сформулировать теоремы о существовании первообразной и о виде первообразной

Первообра́зной или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

(теорема существования) Любая непрерывная на X функция 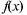имеет первообразную F(x) на X: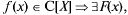

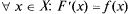
Функция 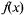на X может иметь бесконечно много первообразных. Так, для 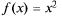первообразной является F(x) =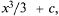

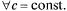
Неопределенный интеграл. Его свойства. Таблица неопределенных интегралов

Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом .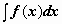
Как следует из изложенного выше, если F(x) - некоторая первообразная функции f(x), то 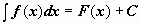, где C - произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением.

Свойства неопределённого интеграла, непосредственно следующие из определения: