Алгоритм метода итерации

· Выбираем начальное приближение .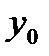

· Вычисляем 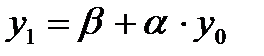, 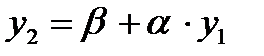и т.д.

· Вычисления проводим до тех пор, пока не будет выполнен критерий сходимости итерационного процесса. Например, .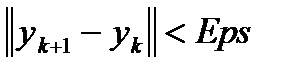

Метод итераций хорошо сходится, если элементы 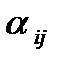малы по абсолютной величине. Иными словами, матрица системы имеет диагональное преобладание.

Аппроксимация и интерполирование функций

Общие понятия

Определение. Аппроксимация - это замена одной функции другой близкой к исходной и обладающей "хорошими" свойствами, позволяющими легко производить над ней те или иные аналитические или вычислительные операции.

Простейшая задача интерполирования: на отрезке [a,b] задана (n+1) точка, эти точки называются узлами интерполирования, и (n+1) значение функции в этих точках. Требуется построить функцию F(x), принадлежащую известному классу и принимающую в узлах интерполирования те же значения, что и f(x), т.е.

.

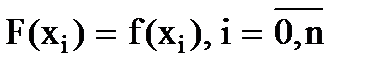Геометрически это означает, что нужно найти кривую некоторого определенного типа, проходящую через систему заданных точек. Это задача становится однозначной, если вместо произвольной функции строить полином P_n(x) степени n такой, что

,

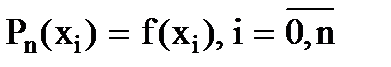тогда внутри промежутков (x_i, x_i+1) построенный полином будет приближенно описывать функцию f(x).

Полученную интерполяционную формулу обычно используют для нахождения приближенного значения функции f(x) в точках, отличных от узлов интерполирования.

Интерполяционный многочлен Лагранжа

Пусть на отрезке [a,b] заданы (n+1) точка x₀, x₁, ¼, x_n и значения функции f в этих точках.

Будем строить интерполяционный многочлен вида 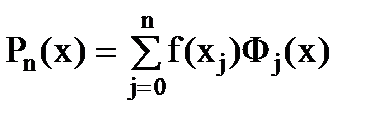, где 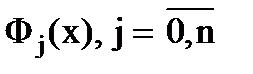- многочлены степени n, удовлетворяющие условиям

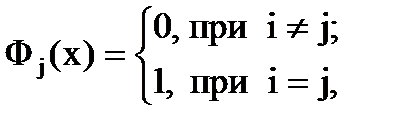
так как требуем, чтобы значения интерполяционного многочлена и значения функции f(x) совпадали в узлах интерполяции i, т.е. .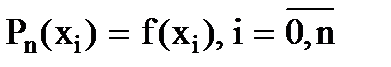

Тогда 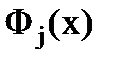можно искать в виде:

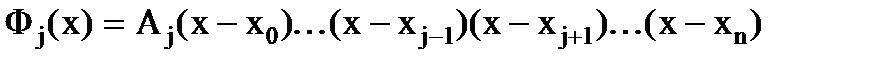
где 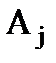- некоторая константа, которую найдем из условия 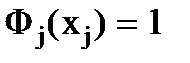, тогда

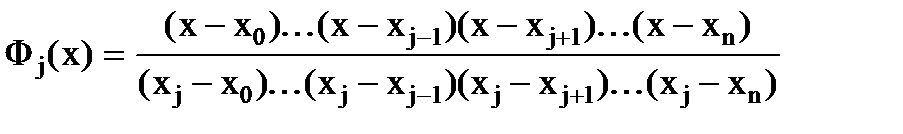
Если обозначить 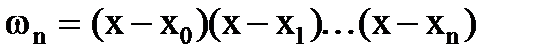и продифференцировать это выражение по х, полагая х=х_j, то последнее выражение можно записать в виде:

,

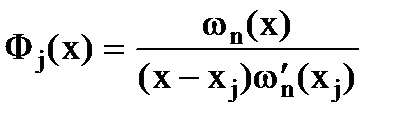где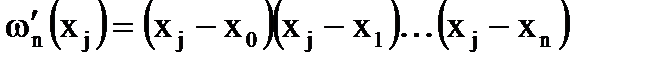

Таким образом, получим многочлен

,

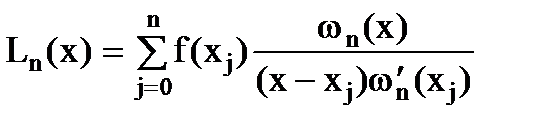который называется интерполяционным многочленом Лагранжа.

Пусть узлы интерполирования являются равноотстоящими, т.е. 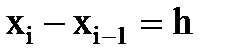, если ввести новую переменную 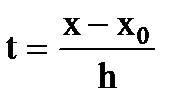, то многочлен Лагранжа для равноотстоящих узлов запишется в виде

,

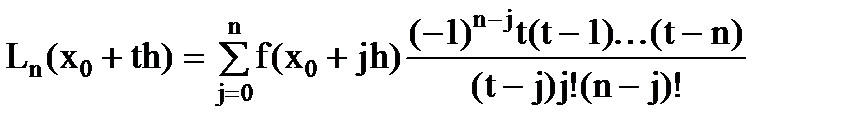т.к. .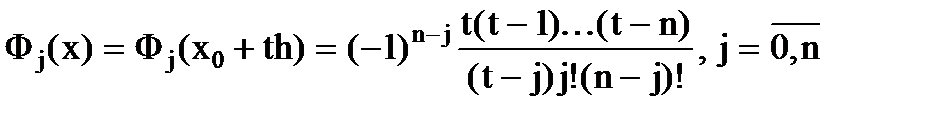

Оценка погрешности интерполяционного многочлена Лагранжа: если функция f(x) имеет на [a,b] непрерывные производные (n+1)-го порядка, имеет вид 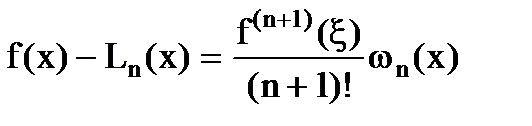, где x - некоторая точка [a,b] или .

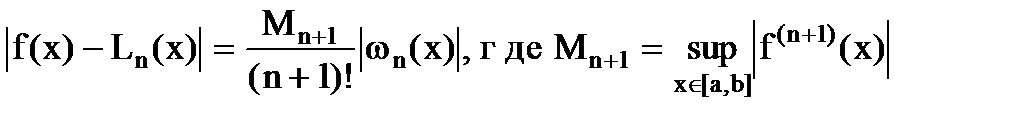Это выражение может служить оценкой отклонения полинома Лагранжа от f(x) в том случае, когда можно оценить 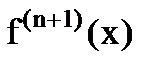.