БИЛЕТ.Уточнение корней методом простой итерации. Теорема, алгоритм геометрическая иллюстрация. Оценка погрешности метода.
Заменим уравнение F(x)=0 равносильным уравнением x = f(x). Теорема.
Пусть уравнение x=f(x) имеет единственный корень на отрезке [a,b] и выполнены условия:
1) функция f(x) определена и дифференцируема на отрезке [a,b];
2) "x Î[a,b] f(x) Î[a,b]
3) $q "xÎ[a,b] |f’(x)|£q<1
Тогда итерационная последовательность xn=f(xn-1) (n=1,2,...) сходится при любом начальном члене x0Î[a,b].
Таким образом, наша задача: преобразовать уравнение F(x)=0 к виду x = f(x), удовлетворяющему условиям теоремы 1-3 (хотя итерационная последовательность может сходиться и при невыполнении некоторых условий).
В зависимости от вида функции сходимость может происходить ступеньками либо по спирали.
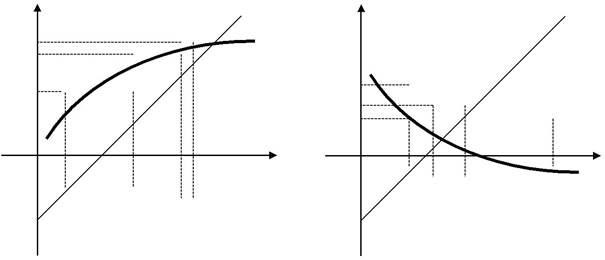
| y | y=x | y | y=x | |||||||||||||||||
| f(x2) | y=f(x) | y=f(x) | ||||||||||||||||||
| f(x1) | ||||||||||||||||||||
| f(x0) | f(x1) | |||||||||||||||||||
| f(x2) | ||||||||||||||||||||
| O | x0 | x1 | x2 x3 | x | f(x0) | |||||||||||||||
| O | x0 x | |||||||||||||||||||
| x1 x3 | x2 |
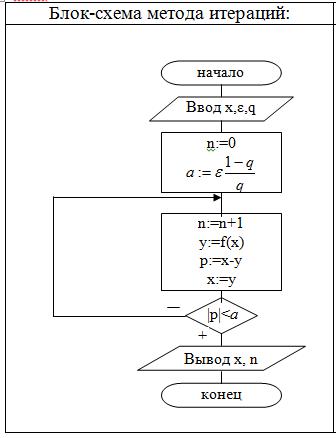
Оценка погрешности метода итераций
Пусть xn – приближение к истинному значению x* корня уравнения x=f(x).
Абсолютная ошибка Dxn=|x*-xn|.
Для оценки погрешности n-го приближения используется формула Dxn
| £ | q n | x - x | . | ||||
| 1 - q | |||||||
Приняв за нулевое приближение xn-1 и учитывая, что при 0<q<1 будет qn<q, для оценки
| погрешности n-го приближения можно использовать формулу Dxn | £ | q | xn - xn-1 | . | ||||
| - q | ||||||||
Значение q можно получить как верхнюю грань модуля производной |f’(x)| при xÎ[a,b].
Чем q меньше, тем быстрее сходится ряд.
| Чтобы | Dxn | £ e достаточно потребовать | q | xn | - xn-1 | £ e , откуда получим условие | ||||
| - q | ||||||||||
окончания счета xn - xn-1 £ e(1- q)


q
Преобразование к итерационному виду
1) Универсальный способ приведения уравнения F(x)=0 к виду x=f(x).
| Уравнение F(x)=0 приводится к равносильному | уравнению x = x – m F(x), | таким | ||||||||||||||||
| образом, f(x) = x – m F(x). | ||||||||||||||||||
| Исходя из третьего условия теоремы: ($q) | ("xÎ[a,b]) [ |f’(x)|£q<1] следует, что должно | |||||||||||||||||
| выполняться неравенство: 0 < |1– mF’(x)| < 1. | ||||||||||||||||||
| Достаточно | подобрать | m так,чтобы выполнялось | неравенство 0<mF’(x)<1, | откуда | ||||||||||||||
| следует m = | и 0 £ | F ¢(x) | £ 1 . | |||||||||||||||
| max F ¢(x) | max F ¢(x) | |||||||||||||||||
| F ¢(x) | = 1 - | min F ¢(x) | . | |||||||||||||||
| Тогда q можно принять q = max | 1 - | |||||||||||||||||
| max F ¢(x) | ||||||||||||||||||
| max F ¢(x) | ||||||||||||||||||
| Примечания: | ||||||||||||||||||
| · | Если ("xÎ[a,b]) | f’(x)<0, | то вместо уравнения F(x)=0 | переходим к | ||||||||||||||
| равносильному уравнению: | – F(x)=0 . | |||||||||||||||||
| · | Если при приведении | уравнения F(x)=0 | к итерационному виду | x=f(x) | ||||||||||||||
| получилось, что "xÎ[a,b] | |f’(x)|>1, то от функции вида y=f(x)переходят к функции | |||||||||||||||||
| x=g(y), | обратной для | f(x). | При этом рассматривается уравнение y=g(y) или | x=g(x), | ||||||||||||||
| причем по свойству обратных функций g ¢(x) = | < 1. | ||
| f ¢(x) | |||
2) Иногда удается преобразовать уравнение F(x)=0 к виду x=f(x) более простым способом, выразив x из уравнения.
6ИЛЕТ.Метод касательных(Ньютона). Сходимость метода, оценка погрешности, геометрическая интерпретация.
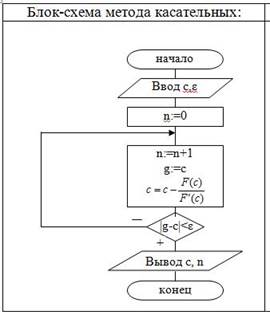
Пусть функция y=F(x) определена, непрерывна, монотонна и дифференцируема в некоторой окрестности корня.Требуется найти корень на отрезке с точностью ε.
На kой итерации проводится касательная к графику функции y=F(x) при x=ck и ищется точка пересечения касательной с осью абсцисс. При этом достаточно задать начальное приближение c0, а не указывать отрезок [a,b].
Уравнение касательной к графику функции y=F(x) в точке x0 имеет вид:
y - F(x0)= F ¢(x0)(x - x0). Пересечение с осью Ox находится из условия y=0, откуда
| x = x0 | - | F (x0) | |
| F ¢(x0) | |||
Таким образом, получим формулу для нахождения последовательности c1, c2… точек
| пересечения касательных с осью абсцисс: ci+1 = ci | - | F (ci ) | |
| F ¢(ci | ) | ||
Условие окончания счета: ci+1 - ci < e


Корень уравнения: ci+1.
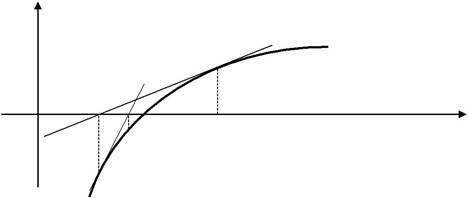
y
y=F(x)
| c1 | c2 | c0 | x | |
| O |
var c,e,g: real;
N:integer;
function f(x: real):real;
begin
{записать, функцию в виде f:=[математическое выражение]}
f:=x*x*x-x+4;end;
function df(x: real):real;
begin {записать, производную функции f в виде
df:=[математическое выражение]} df:=3*x*x-1;end; begin
write('Введите начальное приближение - c: ');readln(c); write('Введите требуемую погрешность - e:'); readln(e);
N:=0;
repeat N:=N+1;
g:=c;
c:=c-f(c)/df(c);
until abs(g-c)<e;
writeln('Приближенное значение корня - Х = ',c); writeln('Число итераций - N = ',N); readln end.
