Основные характеристики графов

ГрафG- это математический объект, состоящий из множества вершинX = {x₁, x₂,..., x_n} и множества реберA = {a₁, a₂,..., a_n}. Таким образом, граф полностью определяется совокупностью множеств X, A: G= (X,A).

Для многих задач несущественно, являются ли ребра отрезками пря­мых или криволинейными дугами; важно лишь то, какие вершины соединяет каждое ребро.

Если ребрам графа приданы направления от одной вершины к другой, то такой граф называется ориентированным. Ребра ориентиро­ванного графа называются дугами. Соответствующие вершины ориентиро­ванного графа называют началоми концом. Если направления ребер не указываются, то граф называется неориентированным (или просто графом).

Пример 3.1.

На рис. 3.1 изображен неориентированный граф G =( X, A).

X= {x₁, x₂, x₃, x₄},

A = {a₁= (x₁, x₂), a₂=(x₂, x₃), a₃=(x₁, x₃), a₄= (x₃, x₄)}.

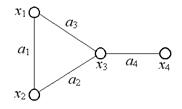
Рис. 3.1.

Пример 3.2.

На рис. 3.2. изображен ориентированный граф G = (X, A).

X = {x₁, x₂, x₃, x₄},

A= {a₁= (x₁,x₂),a₂= (x₁,x₃),a₃= (x₃,x₄),a₄= (x₃,x₂)}.

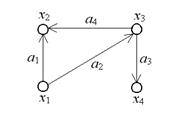
Рис. 3.2.

Граф, имеющий как ориентированные, так и неориентированные ребра, называется смешанным.

Различные ребра могут соединять одну и ту же пару вершин. Такие ребра называют кратными.Граф, содержащий кратные ребра, называется мультиграфом.

Неориентированное ребро графа эквивалентно двум противоположно направленным дугам, соединяющим те же самые вершины.

Ребро может соединять вершину саму с собой. Такое ребро называет­ся петлей. Граф с кратными ребрами и петлями называетсяпсевдографом.

Множество ребер графа может быть пустым. Множество вершин графа не может быть пустым.

Пример 3.3.

На рис. 3.3. изображен ориентированный граф G = (X, A).

X = {x₁, x₂,x₃, x₄},

A= .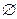

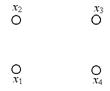
Риc. 3.3.

Как в случае ориентированного, так и в случае неориентированного ребра говорят, что вершины xи yинцидентныребру a, если эти вершины соединены a.

Две вершины называются смежными, если они инцидентны одному и то­му же ребру. Два ребра называются смежными, если они имеют общую вер­шину.

Степеньювершины графа называется число ребер, инцидентных этой вершине. Вершина, имеющая степень 0, называется изолированной, а сте­пень 1 – висячей.

Для ориентированного графа множество вершин, в которые ведут дуги, исходящие из вершины х, обозначают G(х), то есть G(х) = { y: ( x y ) 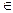G}. Множество G(x) называют образомвершины x. Соответс­твенно G^-1(у)– множество вершин, из которых исходят дуги, ведущие в вершину у, G^-1(y)= {x: ( x , y ) 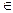G}. Множество G^-1(у)называют прообразом вершины y.

Пример 3.4.

В графе, изображенном на рис. 3.1, концами ребра a₁являются вер­шины x₁, x₂; вершина x₂инцидентна ребрам a₁, a₂; степень вершины x₃равна3; вершины x₁и x₃смежные; ребра a₁и a₂смежные; вершина x₄висячая. В ориентированном графе, изображен­ном на рис. 3.2, началом дуги a₁является вершина x₁, а ее концом - вершина x₂; вершина x₁инцидентна дугам a₁и a₂; G(x₁) = {x₂, x₃}, G(x₂) =Æ, G^-1(x₃) = {x₁}, G^-1(x₁) = Æ.

Подграфомнеориентированного графа G называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G. Аналогично определяется подграф ориентированного графа. Подграф называется собственным, если он отличен от самого графа,

Граф G = (X, A)- полный, если для любой пары вершин x_i и x_j су­ществует ребро (x_i, x_j).

Граф G = (X, A)- симметрический, если для любой дуги (x_i, x_j) существует противоположно ориентированная дуга(x_j, x_i).

Граф G = (X, A) -планарный, если он может быть изображен на плоскости так, что не будет пересекающихся дуг.

Неориентированный граф G = (X, A)– двудольный, если множество его вершин X можно разбить на два такие подмножества X₁и X₂, что каж­дое ребро имеет один конец в X₁, а другой в X₂.