Понятие графа. Способы изображения графов. Способы представления графов.

Граф - это двойка <V, E>, где V - непустое множество вершин, а Е - множество ребер, соединяющих эти вершины попарно. Две вершины, связанные между собой ребром, равноправны, и именно поэтому такие графы называются неориентированными: нет никакой разницы между "началом" и "концом" ребра.

Говоря простым языком, граф - это множество точек (для удобства изображения - на плоскости) и попарно соединяющих их линий (не обязательно прямых). В графе важен только факт наличия связи между двумя вершинами. От способа изображения этой связи структура графа не зависит.

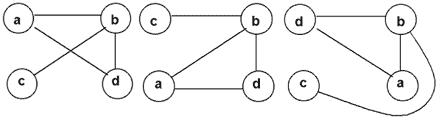
Рис. 11.1. Три способа изображения одного графа

Из приведенного выше определения вытекает, что в графах не бывает петель - ребер, соединяющих некоторую вершину саму с собой. Кроме того, в классическом графе не бывает двух различных ребер, соединяющих одну и ту же пару вершин.

Любому ребру инцидентно ровно две вершины, а вот вершине может быть инцидентно произвольное количество ребер, это количество и определяет степень вершины. Изолированная вершина вообще не имеет инцидентных ей ребер (ее степень равна 0).

Две вершины называются смежными, если они являются разными концами одного ребра (иными словами, эти вершины инцидентны одному ребру). Аналогично, два ребра называются смежными, если они инцидентны одной вершине.

Путь в графе - это последовательность вершин (без повторений), в которой любые две соседние вершины смежны. Например, в графе, изображенном на рис. 11.1, есть два различных пути из вершины a в вершину с: adbc и abc.

Вершина v достижима из вершины u, если существует путь, начинающийся в u и заканчивающийся в v.

Граф называется связным, если все его вершины взаимно достижимы.

Компонента связности - это максимальный связный подграф. В общем случае граф может состоять из произвольного количества компонент связности. Заметим, что любая изолированная вершина является отдельной компонентой связности. На рис. 11.4 изображен граф, состоящий из четырех компонент связности: [abhk], [gd], [c] и [f].

Длина пути - количество ребер, из которых этот путь состоит. Например, длина уже упомянутых путей adbc и abc (см. рис. 11.1) - 3 и 2 соответственно.

Расстояние между вершинами u и v - это длина кратчайшего пути от u до v. Из этого определения видно, что расстояние между вершинами a и c в графе на рис. 11.1 равно 2.

Цикл - это замкнутый путь. Все вершины в цикле, кроме первой и последней, должны быть различны. Например, циклом является путь abda в графе на рис. 11.1.

Эйлеров граф - это граф, в котором существует путь или цикл, содержащий все ребра графа (вершины могут повторяться). Именно такие графы положительно решают упомянутую в начале лекции задачу о кенигсбергских мостах.

Ориентированные графыОрграф - это граф, все ребра которого имеют направление. Такие направленные ребра называются дугами. На рисунках дуги изображаются стрелочками

В отличие от ребер, дуги соединяют две неравноправные вершины: одна из них называется началом дуги (дуга из нее исходит), вторая - концом дуги (дуга в нее входит). Можно сказать, что любое ребро - это пара дуг, направленных навстречу друг другу.

Если в графе присутствуют и ребра, и дуги, то его называют смешанным.

Взвешенные графывзвешенный (другое название: размеченный) граф (или орграф) - это граф (орграф), некоторым элементам которого (вершинам, ребрам или дугам) сопоставлены числа. Наиболее часто встречаются графы с помеченными ребрами. Числа-пометки носят различные названия: вес, длина, стоимость.

Способы представления графов

Матрица смежности

Матрица смежности Sm - это квадратная матрица размером NxN (N - количество вершин в графе), заполненная единицами и нулями по следующему правилу:

Если в графе имеется ребро e, соединяющее вершины u и v, то Sm[u,v] = 1, в противном случае Sm[u,v] = 0.

Заметим, что данное определение подходит как ориентированным, так и неориентированным графам: матрица смежности для неориентированного графа будет симметричной относительно своей главной диагонали, а для орграфа - несимметричной.

Задать взвешенный граф при помощи матрицы смежности тоже возможно. Необходимо лишь внести небольшое изменение в определение:

Если в графе имеется ребро e, соединяющее вершины u и v, то Sm[u,v] = ves(e), в противном случае Sm[u,v] = 0.

Небольшое затруднение возникнет в том случае, если в графе разрешаются ребра с весом 0. Тогда придется хранить два массива: один с нулями и единицами, которые служат показателем наличия ребер, а второй - с весами этих ребер.

Удобство матрицы смежности состоит в наглядности и прозрачности алгоритмов, основанных на ее использовании. А неудобство - в несколько завышенном требовании к памяти: если граф далек от полного, то в массиве, хранящем матрицу смежности, оказывается много "пустых мест" (нулей). Кроме того, для "общения" с пользователем этот способ представления графов не слишком удобен: его лучше применять только для внутреннего представления данных.

Список ребер

Этот способ задания графов наиболее удобен для внешнего представления входных данных. Пусть каждая строка входного файла содержит информацию об одном ребре (дуге):

<номер_начальной_вершины> <номер_конечной_вершины> [<вес_ребра>]

Если задается ориентированный граф, то номера вершин понимаются как упорядоченная пара, а если граф неориентированный - как неупорядоченная.

Списки смежности

Этот способ задания графов подразумевает, что для каждой вершины будет указан список всех смежных с нею вершин (для орграфа - список вершин, являющихся концами исходящих дуг). Конкретный формат входного файла, содержащего списки смежности, необходимо обговорить отдельно. Например, в нашем случае начальная вершина отделена от списка смежности двоеточием:

<номер_начальной_вершины>: <номера_смежных_вершин>

Наиболее естественно применять этот способ для задания орграфов, однако и для остальных вариантов он тоже подходит.

Иерархический список

Собственно, этот способ представления графов является всего лишь внутренней реализацией списка смежности: в одном линейном списке содержатся номера "начальных вершин", а в остальных - номера смежных вершин или указатели на эти вершины

Очевидное преимущество такого способа представления графов заключается в экономичном использовании памяти. И даже небольшая избыточность данных, к которой приходится прибегать в случае неориентированного графа, задавая каждое ребро как две дуги, искупается гибкостью всей структуры, что особенно удобно при необходимости частых перестроений в процессе работы программы.

Граф - динамич.структура. у вершин может быть сколько угодно потомков. Дугами может быть связана любая вершина (допускаются циклы). Используется в задачах искусственного интеллекта , для анализа программ, маршрутизация в комп.сетях и мн.др.

Способы представления:

· Матричное

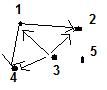
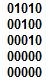матрица смежности [1..n,1..n]

Матрица инциденций [m*n], где m –кол-во дуг, n- вершин.

Матрица циклов (задают перечень циклов в графе и указывают для каждого цикла перечень входящих вершин)

Type refnode=^node;

Refarc=^arc;

Node=record

Id: integer;

Infnode: integer;

Next: refnode;

Arclist: refarc;

End;

Arc=record

Infarct: integer;

Next: refarc;

Adj: refnode;

End;

86 Реализация алгоритмов обхода графа.

Дуги (a,b) и (a`,b`) называются смежными, если конец первой дуги совпадает с началом второй дуги: b=a`. Маршрутом P длины n в графе G называется последовательность n смежных дуг: для i=1..n–1 дуга P[i] смежна с дугой P[i+1]. Начало a первой дуги маршрута будем называть его началом, конец b последней дуги маршрута – его концом, сам маршрут – [a,b]-маршрутом. Пустой последовательности дуг соответствует маршрут нулевой длины, начало и конец которого совпадают. Маршрут будем называть обходом, если он содержит все дуги графа.

Алгоритмом движения по графу будем называть алгоритм, который в процессе своей работы строит маршрут в графе. Формально такой алгоритм можно определить как специальный вид машины с абстрактным состоянием (машина Гуревича, ASM – Abstract State Machine [26]), в котором внешние операции частично специфицированы заданием графа, на котором происходит работа алгоритма, и текущей вершины в нем. Для наших целей достаточно указать, что алгоритму предоставляются две специальные внешние операции status(), возвращающая идентификатор текущей вершины, и call(x), которая осуществляет переход из текущей вершины a по дуге со стимулом x. Для детерминированного графа такая дуга (a,x,b)единственная (единственна вершина b). Предусловием операции call(x) является допустимость стимула x в текущей вершине a. Маршрут строится алгоритмом как последовательность дуг, проходимых последовательными вызовами операции call. Следует отметить, что никакая внешняя операция (не говоря уже о внутренней) не меняет сам граф, и единственной модифицирующей операцией, которая может изменить текущую вершину, является операция call.

Неизбыточным алгоритмом будем называть алгоритм движения по графу, который зависит только от пройденной части графа и допустимости стимулов в текущей вершине. Допустимость стимулов алгоритм может определить с помощью специальной внешней операции next(), которая возвращает стимул, неспецифицированным образом выбираемый среди не выбранных ранее стимулов, допустимых в текущей вершине, осуществляя тем самым итерацию стимулов в вершине. Если все стимулы, допустимые в текущей вершине, уже выбирались, будем считать, что next() возвращает «пустой» символ .

Свободным алгоритмом будем называть неизбыточный алгоритм, который узнает о допустимости стимула, еще не опробованного в текущей вершине a, не заранее, а одновременно с проходом по дуге, раскрашенной этим стимулом. Иначе говоря, свободный алгоритм осуществляет первичный проход по любой еще не пройденной дуге с началом в текущей вершине, используя совмещенную внешнюю операцию nextcall(): x=next(); if x then call(x); return x else return  end. Эта операция неспецифицированным образом выбирает еще не опробованный в текущей вершине a стимул x и проходит по дуге (a,x,b). Если все стимулы уже опробованы в текущей вершине, возвращается пустой символ . Для вторичного прохода по дуге (a,x,b), по-прежнему, используется операция call(x) в тот момент, когда текущей вершиной является вершина a.

Алгоритм предназначен для решения той или иной задачи; такой задачей является обход графа. . В момент остановки алгоритм может сообщить, выполнен обход или нет. Возможен также случай, когда построенный маршрут является обходом, но алгоритм об этом «не знает». Противоположный случай, когда обход не выполнен и алгоритм «знает», что в данном графе вообще нет обхода. Подобную информацию, сообщаемую алгоритмом в момент остановки, будем называть вердиктом алгоритма. Мы будем говорить, что вердикт достоверен, если сообщаемая в нем информация соответствует действительности.

Работа алгоритма, вообще говоря, зависит от выполнения внешних операций; для неизбыточных алгоритмов – от операции next, которая определена неоднозначно. Будем говорить, что алгоритм совершает гарантированный обход данного графа с данной начальной вершиной, если это происходит при любом допустимом выполнении всех внешних операций; для неизбыточных алгоритмов – независимо от итерации стимулов в вершинах (next).

Обход графа

Сильно-связные графы

Вершина b достижима из вершины a, если существует [a,b]-маршрут. Граф сильно-связен, если из каждой его вершины достижима каждая его вершина. Путем называют маршрут без повторного вхождения вершин.

Теорема 3.1: 1) Для любого сильно-связного графа и любой пары его вершин a и b всегда существует [a,b]-обход с длиной O(nk). 2) Для любых n и k существует сильно-связный граф с числом вершин n и числом дуг k`k, в котором любой обход имеет длину (nk`).

1) Произвольным образом линейно упорядочим все дуги графа так, чтобы первая дуга начиналась в вершине a, а последняя дуга заканчивалась в вершине b. Для двух последовательных дуг (v_i,v_i`) и (v<sub>i+1</sub>,v<sub>i+1</sub>`) в сильно-связном графе всегда существует маршрут из конца v_i` i-ой дуги в начало i+1-ой дуги v<sub>i+1</sub>. Удаляя из него циклы, получаем, путь P<sub>i</sub>, ведущий из v<sub>i</sub>` в v_i+1. Искомый обход представляет собой конкатенацию дуг и путей: (v₁,v₁`)^P<sub>1</sub>^…^(v<sub>i</sub>,v<sub>i</sub>`)^P_i^…^P_k–1^(v_k,v_k`), где v₁=a и v_k=b. Поскольку длина пути в графе не превосходит n–1, обход имеет длину не более k+(n–1)(k–1)=n(k–1)+1, то есть, O(nk).

2) Пример графа приведен на рис.1, где p=k`/n – полустепень выхода каждой вершины.

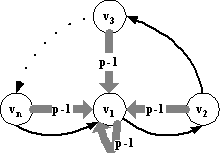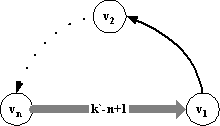Рис.1	Рис.2

Обход этого графа можно представить в виде конкатенации маршрутов P₁,…,P_t, причем каждый из P₁,…,P_t-1 заканчивается дугой (v_i,v₁), где i>1, а каждый из P₂,…,P_t-1 начинается в v₁. Каждый маршрут из P₂,…,P_t-1, заканчивающийся дугой (v_i,v₁) имеет длину i, а их число равно p-1. Поэтому, считая, что маршрут P₁заканчивается дугой (v_j,v₁) и имеет длину не менее 1, и не учитывая последний маршрут P_t, получаем нижнюю оценку длины обхода
(p–1)+2(p–1)+…+n(p–1)–j+1 = (p–1)n(n–1)/2 –j+1  (p–1)n(n–1)/2–n+1 = L. Нам достаточно, чтобы для некоторой константы C>0 при любом n>0 выполнялось L  Cpn² = Ck`n. Легко показать, например, что это так для C=1/3 и p3. Тем самым, мы определяем k` = max{k,3n}.

Заметим, что в примере на рис.1 полустепени выхода у всех вершин одинаковые. Это сделано для того, чтобы не накладывать на число стимулов ограничений снизу, кроме необходимого k`/n. Без этого требования пример можно упростить, заменив все дуги, ведущие из v<sub>i</sub> в v<sub>1</sub> на дуги, ведущие из v<sub>n</sub> в v<sub>1</sub>, что требует k`–n+1стимулов (рис.2).