Уравнения равновесия пространственной системы сил
Как было выяснено в § 4.4, необходимые и достаточные условия равновесия пространственной системы сил, приложенных к твердому телу, можно записать в виде трех уравнений проекций (4.16) и трех моментов (4.17):
, 
, 
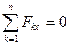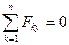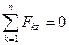, (7.13)
, 
, 
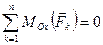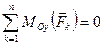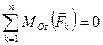. (7.14)
Если тело полностью закреплено, то действующие на него силы находятся в равновесии и уравнения (7.13) и (7.14) служат для определения опорных реакций. Конечно, могут встретиться случаи, когда этих уравнений недостаточно для определения опорных реакций; такие статически неопределимые системы мы рассматривать не будем.
Для пространственной системы параллельных сил уравнения равновесия принимают вид (§ 4.4[‡]):
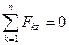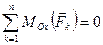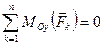, , . (7.15)
Рассмотрим теперь случаи, когда тело закреплено лишь частично, т.е. связи, которые наложены на тело, не гарантируют равновесия тела. Можно указать четыре частных случая.
1. Твердое тело имеет одну неподвижную точку. Иначе говоря, оно прикреплено к неподвижной точке при помощи идеального сферического шарнира.
Поместим в эту точку начало неподвижной системы координат. Действие связи в точке А заменим реакцией; так как она неизвестна по модулю и по направлению, то мы ее представим в виде трех неизвестных составляющих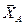 
, 
, 
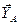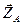, направленных соответственно вдоль осей 
, 
, 
.
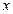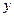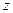Уравнения равновесия (7.13) и (7.14) в этом случае запишутся в виде:
1) 
,
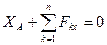2) 
,
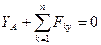3) 
,
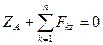4) 
,
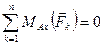5) 
,
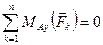6) 
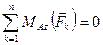. (7.16)
Последние три уравнения не содержат составляющих реакции, так как линия действия этой силы проходит через точку А. Следовательно, эти уравнения устанавливают зависимости между активными силами, необходимыми для равновесия тела, причем три первых уравнения могут быть использованы для определения составляющих реакции.
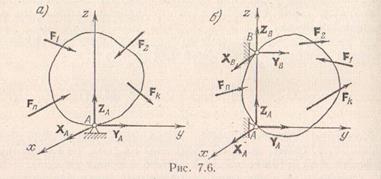
Таким образом, условием равновесия твердого тела, имеющего одну неподвижную точку, является равенство нулю каждой из алгебраических сумм моментов всех активных сил системы относительно трех осей, пересекающихся в неподвижной точке тела.
2. Тело имеет две неподвижные точки. Это, например, будет иметь место, если оно прикреплено к двум неподвижным точкам при помощи шарниров.
Выберем начало координат в точке А и направим ось 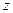вдоль линии, проходящей через точки А и В. Заменим действие связей реакциями, направив составляющие реакции вдоль координатных осей. Обозначим расстояние между точками А и В через а; тогда уравнения равновесия (7.13) и (7.14) запишутся в следующем виде:
1) 
,
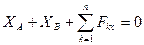2) 
,
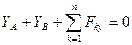3) 
,
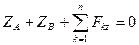4) 
,
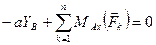5) 
,
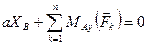6) 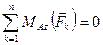. (7.17)
Последнее уравнение не содержит сил реакции и устанавливает связь между активными силами, необходимую для равновесия тела. Следовательно, условием равновесия твердого тела, имеющего две неподвижные точки, является равенство нулю алгебраической суммы моментов всех активных сил, приложенных к телу, относительно оси, проходящей через неподвижные точки. Первые пять уравнений служат для определения неизвестных составляющих реакций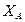 
, 
, 
, 
, 
, 
.
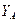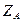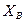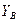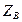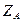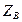Заметим, что составляющие и не могут быть определены в отдельности. Из третьего уравнения определяется только сумма 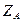+ 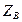и, следовательно, задача в отношении каждого из этих неизвестных для твердого тела является статически неопределимой. Однако, если в точке В находится не сферический, а цилиндрический шарнир (т.е. подшипник), не препятствующий продольному скольжению тела вдоль оси вращения, то 
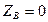и задача становится статически определимой.
Тело имеет неподвижную ось вращения, вдоль которой оно может скользить без трения. Это значит, что в точках А и В находятся цилиндрические шарниры (подшипники), причем составляющие их реакций вдоль оси вращения равны нулю. Следовательно, уравнения равновесия примут вид:
1) ,
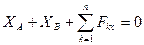2) ,
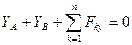3) ,
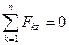4) ,
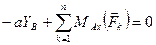5) ,
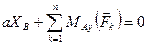6) 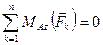. (7.18)
Два из уравнений (7.18), а именно, третье и шестое, накладывают ограничения на систему активных сил, а остальные уравнения служат для определения реакций.
Тело опирается в трех точках на гладкую поверхность, причем точки опоры не лежат на одной прямой. Обозначим эти точки через А, В и С и совместим с плоскостью АВС координатную плоскость Аху. Заменив действие связей вертикальными реакциям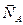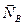и 
, 
и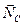 
, запишем условия равновесия (7.14) в таком виде:
1) 
,
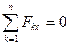2) 
,
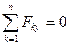3) 
,
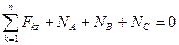4) 
,
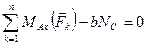5) 
,
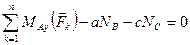6) 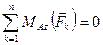. (7.19)
Третье – пятое уравнения могут служить для определения неизвестных реакций, а первое, второе и шестое уравнения представляют собой условия, связывающие активные силы и необходимые для равновесия тела. Конечно, для равновесия тела необходимо выполнение условий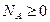 
, 
, 
, 
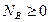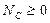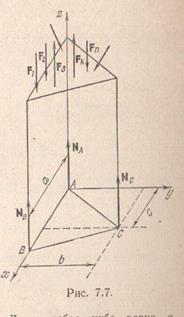так как в точках опоры могут возникнуть только реакции принятого выше направления.
Если тело опирается на горизонтальную плоскость более чем в трех точках, то задача становится статически неопределимой, так как при этом реакций будет столько, сколько точек, а уравнений для определения реакций останется только три.
Задача 7.3. Найти главный вектор и главный момент системы сил, изображенной на рис. Силы приложены к вершинам куба и направлены вдоль его ребер, причем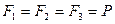 
, 
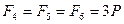. Длина ребра куба равна а.
Проекции главного вектора находим по формулам (4.4):
, 
, 
.
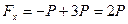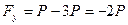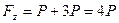Его модуль равен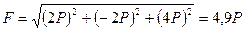 
. Направляющие косинусы будут
, 
;
, 
;
, 
.
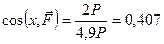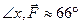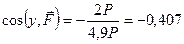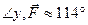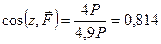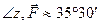Главный вектор изображен на рис.
Далее находим проекции главного момента по формулам (4.7):
,
,
,
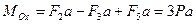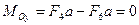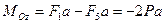а модуль главного момента по формуле (4.8)
.
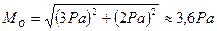Теперь определим направляющие косинусы главного момента:
, 
;
, 
;
, 
.
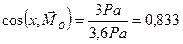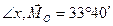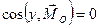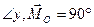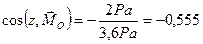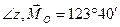Главный момент изображен на рис. Угол между векторам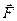и 
и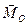 
вычисляется по формуле (4.11)
.
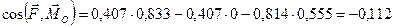Следовательно, угол между этими векторами равен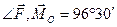 
.
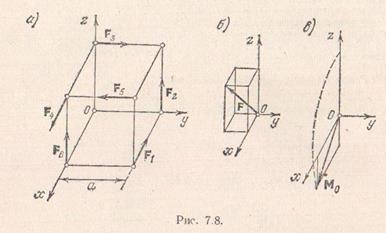
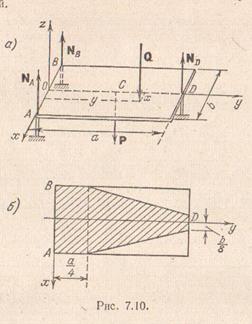
Задача 7.5.Прямоугольная пластина тремя ножками опирается на гладкий пол. Вес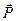 
пластины приложен в ее центре. Длина и ширина пластина соответственно 
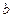и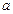 
. В точке с координатам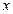и и 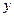к пластине приложена вертикальная сила 
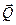. Определить область, внутри которой можно брать точки приложения силы 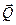, чтобы пластина не опрокинулась. Определить также, при каком соотношении между модулями сил 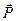и 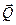вся поверхность пластины будет безопасной.
Решение. Заменяя действие пола вертикальными реакциями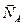 
, 
, 
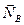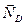, составим уравнения равновесия. Так как все силы, действующие на пластину, параллельны, то можно воспользоваться уравнениями (7.15):
,
,
.
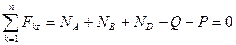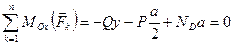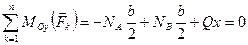Отсюда
,
,
.
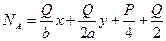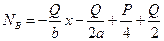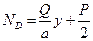Для того, чтобы пластина не опрокинулась, необходимо выполнение условий:
, 
.
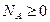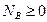Границы искомой области найдем из условий:
,
.
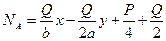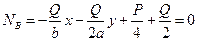Отсюда находим
,
.
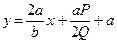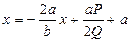На рис. искомая область, построенная при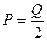 
, заштрихована. При 
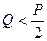вся поверхность пластины будет безопасной.
Глава 8