Производная степенно-показательной функции
Используя правило дифференцирования неявной функции можно находить производные некоторых сложных функций.
Задание 29.Найти производную степенно-показательной функции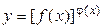 
, в которой основание степени и показатель степени являются некоторыми функциями аргумента х.
Решение. Прологарифмируем заданную функцию:
.
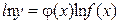Производную y' будем искать, дифференцируя полученное выражение по правилу дифференцирования неявной функции:
,
.
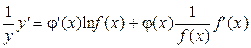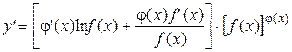Окончательно для производной степенно-показательной функции можно записать:
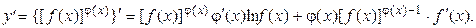
Из полученной формулы видно, что вначале степенно-показательную функцию мы рассматриваем как показательную со сложным показателем степени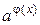 
, где a = f(x) и первое слагаемое получаем при дифференцировании заданной функции по правилу нахождения производной показательной функции:
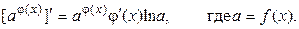
Второе слагаемое получаем при дифференцировании степенно-показательной функции как сложной степенной функции [f(x)]n, где n = φ(x).
В результате дифференцирования сложной степенной функции получаем второе слагаемое
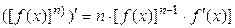, где n = φ(x).
Задание 30.Найти производную функции:
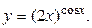
Решение. Данная функция является степенно-показательной функцией. Для заданной функции обозначим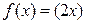 
, 
, 
, 
.
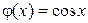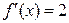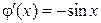Для производной заданной функции по формуле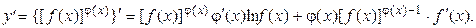
получим:
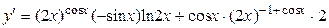
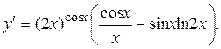
Производная функции, заданной параметрически.
При параметрическом задании функции зависимость функции у от аргумента х задается двумя уравнениями y = f(t); x = φ(t).
Производная функции, заданной параметрически вычисляется в следующем порядке.
1. Находим производную функции у по параметру t:
.
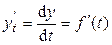2. Находим производную аргумента х по параметру t:
.
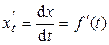3. Находим производную функции у по параметру х:
.
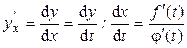Задание 31. Найти значение производной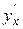 
функции заданной уравнениями:
y = t cost; x = t (1 – sint),
при t = π.
Решение. Находим производную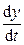 
,
.
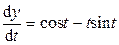Находим производную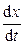 
,
.
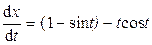Находим производную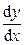 
,
.
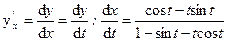Находим значение производной 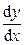при t = π:
.
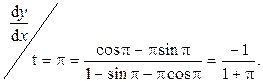Задание 32.Найти производную функции, заданной в параметрическом виде:
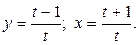
Решение. Находим производную 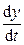по формуле 
.
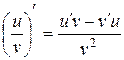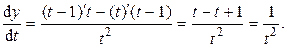
Находим производную :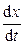
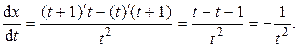
Находим производную :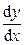
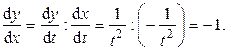
Задание 33.Найти производную второго порядка от функции:
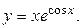
Решение. Находим производную первого порядка:
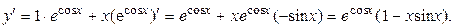
Еще раз дифференцируем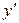 
и получим производную второго порядка:
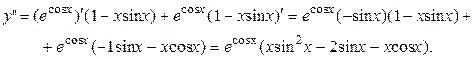
Найти самостоятельно производную функции:
а) 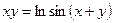 | б)  | |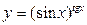
a) 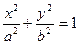 | б)  | |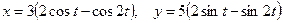
Ответы
1а)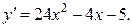 
1б)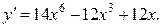 
2а)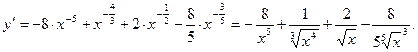 
2б)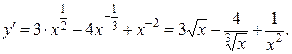 
3а)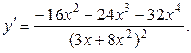 
Можно упростить выражение до нахождения производной, сократив на х, тогда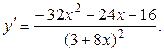 
3б)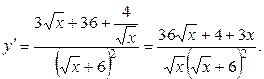 
4а)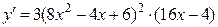 
.
4б)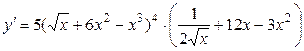 
.
5а)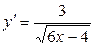 
.
5б)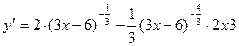 
, если решать по формуле производной произведения.
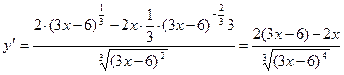, если решать по формуле производной частного.
После преобразования получим:
.
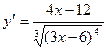6а)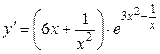 
.
6б)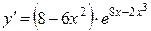 
.
7а)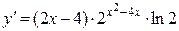 
.
7б)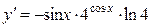 
.
8а)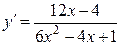 
.
8б)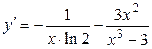 
.
9а)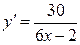 
.
9б)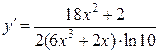 
.
10а)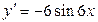 
.
10б)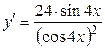 
.
11а)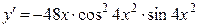 
.
11б)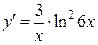 
.
12а)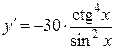 
.
12б)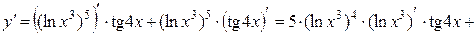 
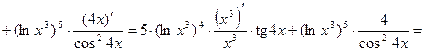
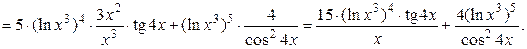
13а)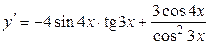 
.
13б)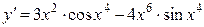 
.
14а)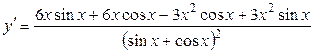 
.
14б)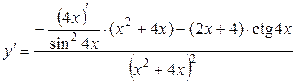 
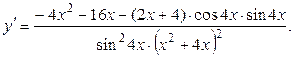
15а)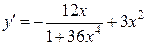 
.
15б)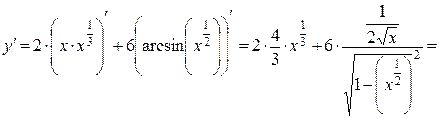 
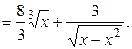
16а)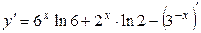 
.
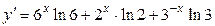16б)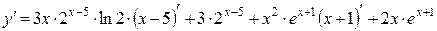 
.
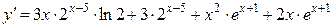17а)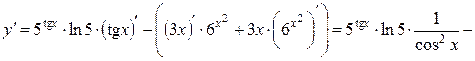 
.
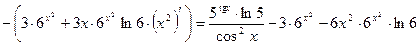17б)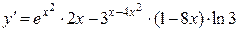 
.
18а)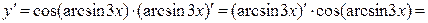 
.
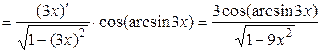18б)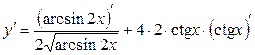 
.
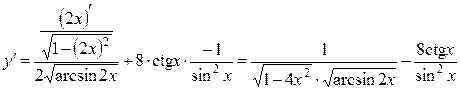19 а
19 б
20 а
20 б