Основные показатели эффективности работы СМО, вычисленные с помощью средств системы MATLAB и результаты моделирования
Условие задачи
На склад с одним бункерным приемным устройством поступабт полувагоны с сыпучими грузами под разгрузку. Интервалы времени между прибытиями подач вагонов – независимые, одинаково распределенные случайные величины, имеющие показательный закон распределения с параметром λ = 4 подачи в сутки. Время разгрузки одной подачи вагонов имеет показательный закон распределения со средним значением четыре с половиной часа. Вместимость путей для ожидания последующими подачами вагонов не ограниченно.
Кодировка Кендалла для данной СМО
M – простейший поток
М – показательный закон распределения
m = 1 – количество обслуживающих устройств
Кодировка Кендалла для данной СМО имеет вид:
М|M|1 с ожиданием λ = 4/24=1/6, μ = 1/4,5
В этой системе обслуживающим устройством является одно бункерное приемное устройство. Клиентом в этой системе являются полувагоны с сыпучими грузами.
Формулы для распределений интервалов во входном потоке и длительности обслуживания
Показательный закон распределения:
A(t) = 1- e-λt
По условию задачи интенсивность λ = 4 подачи/сутки, тогда:
A(t) = 1- e-4t, t ≥ 0
Пусть v1,v2, . . . vk – время разгрузки одной подачи вагонов
B(t) = P(vk ≤ t) = 1- e-μt
Среднее время разгрузки одной подачи вагонов 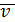 = 4,5 ч.
= 4,5 ч.
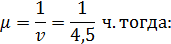
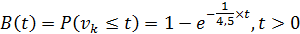
Диаграмма интенсивностей переходов между состояниями
Инфинитезимальной матрицей однородной марковской цепи (цепи в непрерывном времени) называется матрица Q, составленная из правых производных в нуле от элементов матрицы P(t) вероятностей перехода за время t.
Инфинитезимальная матрица имеет следующий вид:
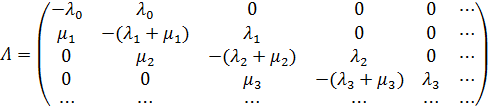
Для СМО вида М|M|1 верно следующее:
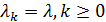
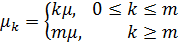
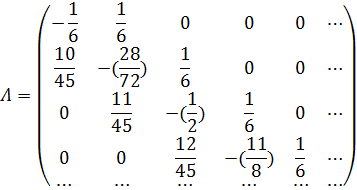
Стохастические графы
 |
1/6 1/6 1/6 1/6




…
10/45 11/45 12/45 12/45
Система дифференциальных уравнений Колмогорова для определения вероятностей состояния СМО в произвольный момент времени
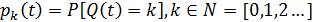
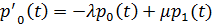
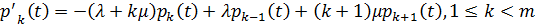
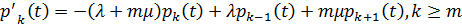
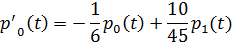
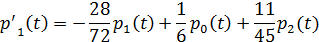
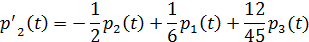
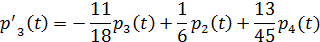
…
Проверка условий наличия стационарного режима
Условие, при котором существует стационарный режим СМО с ожиданием:
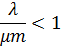
Загрузка системы:
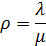
Загрузка СМО, приходящаяся на один прибор:
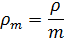
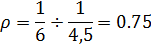
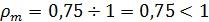
Вывод: рm < 1 значит данная система имеет стационарный режим.
Системы уравнений для определения стационарных вероятностных состояний
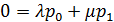
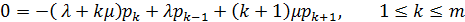
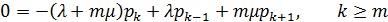
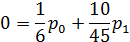
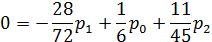
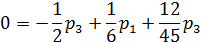
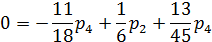
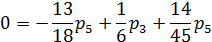
Решение системы в п.7, т.е. стационарные вероятности состояний СМО
В частном случае системы М|M|1|∞ :
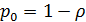 – вероятность простоя;
– вероятность простоя;
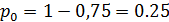
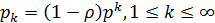 - вероятность стационарного состояния;
- вероятность стационарного состояния;
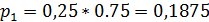
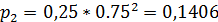
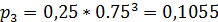
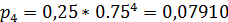
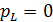 ;
;
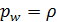 – вероятность того, что требование будет обслужено после некоторого ожидания;
– вероятность того, что требование будет обслужено после некоторого ожидания;
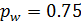
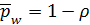 – вероятность того, что поступившее требование будет обслужено без ожидания;
– вероятность того, что поступившее требование будет обслужено без ожидания;
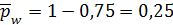
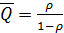 – среднее число требований, находящихся в СМО;
– среднее число требований, находящихся в СМО;
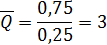
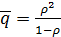 – среднее число требований, находящихся в очереди;
– среднее число требований, находящихся в очереди;
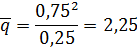
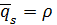 – среднее число занятых приборов
– среднее число занятых приборов
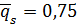
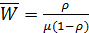 –среднее время ожидания начала обслуживания;
–среднее время ожидания начала обслуживания;
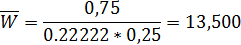
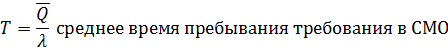
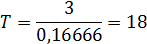
Основные показатели эффективности работы СМО, вычисленные с помощью средств системы MATLAB и результаты моделирования
Вычисление числовых характеристик открытой марковской системы M|M|1 с ожиданием
%Ввод исходных данных
lambda=4/24; mu=1/4.5;
m=1;
rho=lambda/mu; rho_m=rho/m;
% Проверка условия существования стационарного режима
if rho_m>=1,
disp('СТАЦИОНАРНОГО РЕЖИМА НЕ СУЩЕСТВУЕТ');
else
disp('СТАЦИОНАРНЫЙ РЕЖИМ СУЩЕСТВУЕТ');
K=input('СКОЛЬКО ВЕРОЯТНОСТЕЙ ВЫЧИСЛЯТЬ?');
while K<=m
disp('K ДОЛЖНО БЫТЬ НЕ МЕНЕЕ m+1');
K=input('СКОЛЬКО ВЕРОЯТНОСТЕЙ ВЫЧИСЛЯТЬ?');
end;
%Вычисление вероятностей
x=1:m;
x1=ones(1,K-1-m)*m;
xx=[x,x1];
slave1=ones(1,K-1)*rho;
slave2=slave1./xx;
slave=cumprod(slave2);
disp('ВЕРОЯТНОСТЬ ПРОСТОЯ');
P0=1/(1+sum(slave(1:m-1))+slave(m)/(1-rho_m)); disp(P0);
disp('ВЕРОЯТНОСТИ СОСТОЯНИЙ 1,...,K-1');
Psost=slave*P0; disp(Psost);
disp('ВЕРОЯТНОСТЬ ОЖИДАНИЯ ПЕРЕД ОБСЛУЖИВАНИЕМ');
Pw=Psost(m)/(1-rho_m); disp(Pw);
disp('ВЕРОЯТНОСТЬ ОБСЛУЖИВАНИЯ БЕЗ ОЖИДАНИЯ');
Pww=1-Pw; disp(Pww);
disp('СРЕДНЕЕ ЧИСЛО ЗАЯВОК В СИСТЕМЕ');
k=1:m-1;
Qsr=k*(Psost(1:m-1))'+m*Pw+Psost(m)*rho_m/(1-rho_m)^2;
disp(Qsr);
disp('СРЕДНЕЕ ЧИСЛО ЗАЯВОК В ОЧЕРЕДИ');
qsr=Psost(m)*rho_m/(1-rho_m)^2; disp(qsr);
disp('СРЕДНЕЕ ЧИСЛО ЗАНЯТЫХ ПРИБОРОВ');
qs=Qsr-qsr; disp(qs);
disp('СРЕДНЕЕ ВРЕМЯ ОЖИДАНИЯ');
W=qsr/lambda; disp(W);
disp('СРЕДНЕЕ ВРЕМЯ ПРЕБЫВАНИЯ В СИСТЕМЕ');
T=Qsr/lambda; disp(T);
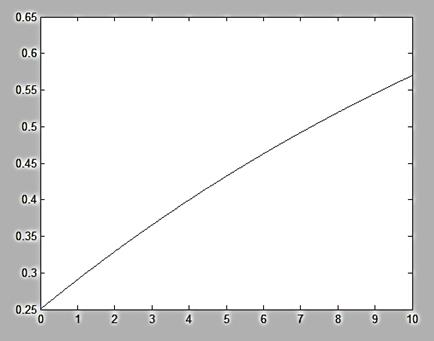
%График функции распределения
t=0:0.01:10;
FW=1-Pw*exp(-(m*mu-lambda)*t);
plot(t,FW);
end;
Результат работы программы:
СТАЦИОНАРНЫЙ РЕЖИМ СУЩЕСТВУЕТ
СКОЛЬКО ВЕРОЯТНОСТЕЙ ВЫЧИСЛЯТЬ?5
ВЕРОЯТНОСТЬ ПРОСТОЯ
0.2500
ВЕРОЯТНОСТИ СОСТОЯНИЙ 1,...,K-1
0.1875 0.1406 0.1055 0.0791
ВЕРОЯТНОСТЬ ОЖИДАНИЯ ПЕРЕД ОБСЛУЖИВАНИЕМ
0.7500
ВЕРОЯТНОСТЬ ОБСЛУЖИВАНИЯ БЕЗ ОЖИДАНИЯ
0.2500
СРЕДНЕЕ ЧИСЛО ЗАЯВОК В СИСТЕМЕ
СРЕДНЕЕ ЧИСЛО ЗАЯВОК В ОЧЕРЕДИ
2.2500
СРЕДНЕЕ ЧИСЛО ЗАНЯТЫХ ПРИБОРОВ
0.7500
СРЕДНЕЕ ВРЕМЯ ОЖИДАНИЯ
13.5000
СРЕДНЕЕ ВРЕМЯ ПРЕБЫВАНИЯ В СИСТЕМЕ
|
Моделирование открытой СМО М|M|1|∞ с ожиданием
clc
lambda=4/24; mu=1/4.5; m=1;
Num=input('Число изменений состояния системы за время моделирования');
s=1;
T=zeros(1,Num);
Qt=zeros(1,Num);
Time=zeros(1,Num);
for i=2:Num,
if Qt(i-1)==0
v=inf;u=-log(rand)/lambda;
else
u=-log(rand)/lambda;
qs=min(m,Qt(i-1));
v=-log(rand)/(qs*mu);
end;
delta_time=min(u,v);
T(i)=T(i-1)+delta_time;
Time(s)=Time(s)+delta_time;
if u<v
Qt(i)=Qt(i-1)+1;
else
Qt(i)=Qt(i-1)-1;
end;
s=Qt(i)+1;
end;
z=zeros(1,Num);
mvect=ones(1,Num)*m;
qt=max(z,Qt-mvect);
subplot(211);plot(T,Qt);
title('СКОЛЬКО КЛИЕНТОВ В СИСТЕМЕ');
subplot(212);plot(T,qt);
title('СКОЛЬКО КЛИЕНТОВ В ОЧЕРЕДИ');
disp('оценки характеристик системы M|M|1 с ожиданием');
disp('полученные на основе моделирования');
Psost=Time/T(Num);
disp('вероятность простоя'); disp(Psost(1));
N=input('Количество вероятностей,которые необходимо вывести на экран');
disp('вероятности состояний 1,...,N'); disp(Psost(2:N+1));
disp('вероятность ожидания'); Pw=1-sum(Psost(1:m)); disp(Pw);
disp('среднее число заявок в системе');
k=0:(Num-1);Qsr=k*Psost'; disp(Qsr);
disp('Среднее число заявок в очереди');
qsr=max(z,k-m)*Psost'; disp(qsr);
Результат работы программы:
Число изменений состояния системы за время моделирования500
оценки характеристик системы M|M|1 с ожиданием
полученные на основе моделирования
вероятность простоя
0.2469
Количество вероятностей,которые необходимо вывести на экран10
вероятности состояний 1,...,N
Columns 1 through 7
0.1588 0.1428 0.1106 0.0825 0.0582 0.0393 0.0322
Columns 8 through 10
0.0519 0.0415 0.0214
вероятность ожидания
0.7531
среднее число заявок в системе
3.0140
Среднее число заявок в очереди
2.2609
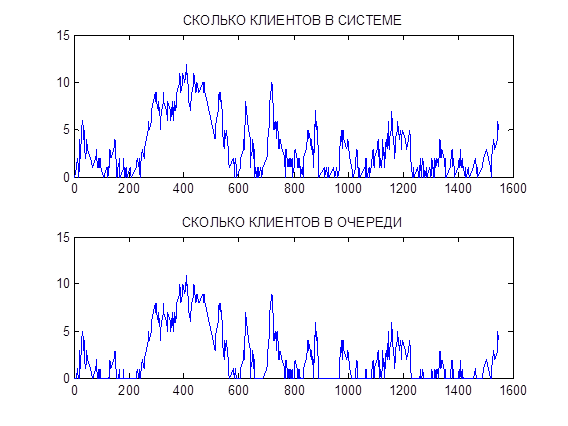
Таблица сравнений
Таблица 1
| Основные характеристики | Результаты расчета в системе MATLAB | Результаты ручного расчета | Результаты на основе моделирования |
| p0 вероятность простоя | 0.2500 | 0.25 | 0,2469 |
| pk вероятность стационарного состояния | 0.1875 0.1406 0.1055 0.0791 | 0.1875 0.1406 0.1055 0.0791 | 0,1588 0,1428 0,1106 0,0825 |
| pw вероятность ожидания перед обслуживанием | 0.7500 | 0.75 | 0.7531 |
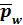 Вероятность обслуживания без ожидания Вероятность обслуживания без ожидания | 0.2500 | 0.25 | - |
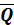 Среднее число заявок в системе Среднее число заявок в системе | 3.0140 | ||
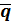 Среднее число заявок в очереди Среднее число заявок в очереди | 2.2500 | 2.25 | 2.2609 |
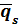 Среднее число занятых приборов Среднее число занятых приборов | 0.7500 | 0.75 | - |
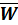 Среднее время ожидания Среднее время ожидания | 13.5000 | 13.5 | - |
| T Среднее время пребывания в системе | - |
