Способы нахождения обратной матрицы

Пусть дана квадратная матрица 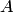. Требуется найти обратную матрицу .

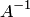Первый способ. В теореме 4.1 существования и единственности обратной матрицы указан один из способов ее нахождения.

1. Вычислить определитель 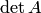данной матрицы. Если 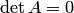, то обратной матрицы не существует (матрица 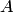вырожденная).

2. Составить матрицу 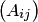из алгебраических дополнений 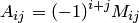элементов матрицы .

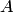3. Транспонируя матрицу 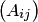, получить присоединенную матрицу .

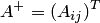4. Найти обратную матрицу (4.1), разделив все элементы присоединенной матрицы на определитель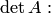

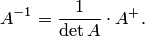
Второй способ. Для нахождения обратной матрицы можно использовать элементарные преобразования.

1. Составить блочную матрицу 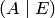, приписав к данной матрице 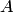единичную матрицу того же порядка.

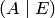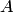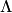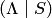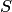2. При помощи элементарных преобразований, выполняемых над строками матрицы , привести ее левый блок к простейшему виду . При этом блочная матрица приводится к виду , где — квадратная матрица, полученная в результате преобразований из единичной матрицы .

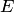3. Если 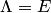, то блок 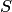равен обратной матрице, т.е. 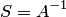. Если 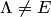, то матрица 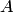не имеет обратной.

В самом деле, при помощи элементарных преобразований строк матрицы 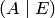можно привести ее левый блок 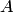к упрощенному виду 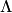(см. рис. 1.5). При этом блочная матрица 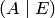преобразуется к виду 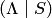, где 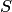— элементарная матрица, удовлетворяющая равенству 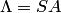. Если матрица 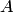невырожденная, то согласно п.2 замечаний 3.3 ее упрощенный вид совпадает с единичной матрицей 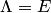. Тогда из равенства 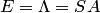следует, что 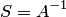. Если же матрица 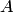вырожденная, то ее упрощенный вид 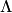отличается от единичной матрицы, а матрица 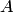не имеет обратной.

11.Матричные уравнения и их решение. Матричная форма записи СЛАУ. Матричный способ (метод обратной матрицы) решения СЛАУ и условия его применимости.

Матричными уравнениями называются уравнения вида :
A*X=C; X*A=C; A*X*B=C где матрица А,В,С известны ,матрица Х не известна, если матрицы А и В не вырождены, то решения исходных матриц запишется в соответственном виде : Х=А^-1 *С; Х=С*А^-1; Х=А^-1*С*В^-1Матричная форма записи систем линейных алгебраических уравнений.С каждой СЛАУ можно связать несколько матриц; более того – саму СЛАУ можно записать в виде матричного уравнения. Для СЛАУ (1) рассмотрим такие матрицы:

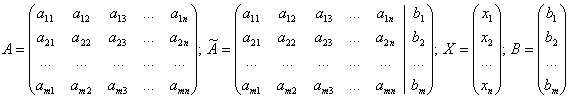
Матрица A называется матрицей системы. Элементы данной матрицы представляют собой коэффициенты заданной СЛАУ.

Матрица A˜ называется расширенной матрицей системы. Её получают добавлением к матрице системы столбца, содержащего свободные члены b1,b2,...,bm. Обычно этот столбец отделяют вертикальной чертой, – для наглядности.

Матрица-столбец B называется матрицей свободных членов, а матрица-столбец X – матрицей неизвестных.

Используя введённые выше обозначения, СЛАУ (1) можно записать в форме матричного уравнения: A⋅X=B.

Примечание

Матрицы, связанные с системой, можно записать различными способами: всё зависит от порядка следования переменных и уравнений рассматриваемой СЛАУ. Но в любом случае порядок следования неизвестных в каждом уравнении заданной СЛАУ должен быть одинаков .

Матричный метод подходит для решения СЛАУ, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы отличен от нуля. Если система содержит больше трех уравнений, то нахождение обратной матрицы требует значительных вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса.

12.Однородные СЛАУ, условия существования их ненулевых решений. Свойства частных решений однородных СЛАУ.

Линейное уравнение называется однородным, если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной и имеет общий вид:

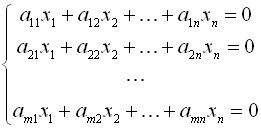
13.Понятие линейной независимости и зависимости частных решений однородной СЛАУ. Фундаментальная система решений (ФСР) и её нахождение. Представление общего решения однородной СЛАУ через ФСР.

Система функций y₁(x), y₂(x), …, y_n(x) называется линейно зависимой на интервале (a, b), если существует набор постоянных коэффициентов 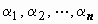, не равных нулю одновременно, таких, что линейная комбинация этих функций тождественно равна нулю на (a, b): 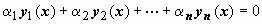для .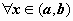
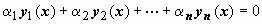Если равенство для 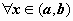возможно только при 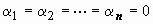, система функций y₁(x), y₂(x), …, y_n(x) называется линейно независимой на интервале (a, b).
Другими словами, функции y₁(x), y₂(x), …, y_n(x) линейно зависимы на интервале (a, b), если существует равная нулю на (a, b) их нетривиальная линейная комбинация. Функции y₁(x),y₂(x), …, y_n(x) линейно независимы на интервале (a, b), если только тривиальная их линейная комбинация тождественно равна нулю на (a, b).

Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.

Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы. Любое решение исходной системы есть линейная комбинация решений ФСР.

Теорема

Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и общего решения соответствующей однородной СЛАУ.

1. Если столбцы 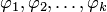— решения однородной системы уравнений, то любая их линейная комбинация 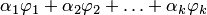также является решением однородной системы.

В самом деле, из равенств 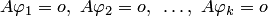следует, что

т.е. линейная комбинация решений является решением однородной системы.

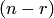2. Если ранг матрицы однородной системы равен , то система имеет линейно независимых решений.

Действительно, по формулам (5.13) общего решения однородной системы найдем 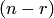частных решений 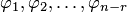, придавая свободным переменным следующие стандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):

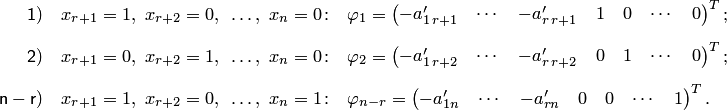
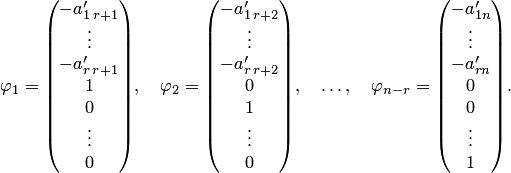
которые линейно независимы. В самом деле, если из этих столбцов составить матрицу, то последние 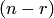ее строк образуют единичную матрицу. Следовательно, минор, расположенный в последних 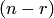строках не равен нулю (он равен единице), т.е. является базисным. Поэтому ранг матрицы будет равен 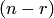. Значит, все столбцы этой матрицы линейно независимы (см. теорему 3.4).

Любая совокупность 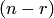линейно независимых решений 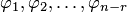однородной системы называется фундаментальной системой (совокупностью) решений.

14Минор 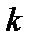-ого порядка, базисный минор, ранг матрицы. Вычисление ранга матрицы.

Минором порядка k матрицы А называется детерминант некоторой ее квадратной подматрицы порядка k.

В матрице А размеров m x n минор порядка r называется базисным, если он отличен от нуля, а все миноры большего порядка, если они существуют, равны нулю.

Столбцы и строки матрицы А, на пересечении которых стоит базисный минор, называются базисными столбцами и строками А.

Теорема 1. (О ранге матрицы). У любой матрицы минорный ранг равен строчному рангу и равен столбцовому рангу.

Теорема 2.(О базисном миноре). Каждый столбец матрицы раскладывается в линейную комбинацию ее базисных столбцов.

Рангом матрицы (или минорным рангом) называется порядок базисного минора или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры. Ранг нулевой матрицы по определению считают 0.

Отметим два очевидных свойства минорного ранга.

1) Ранг матрицы не меняется при транспонировании, так как при транспонировании матрицы все ее подматрицы транспонируются и миноры не меняются.

2) Если А’-подматрица матрицы А, то ранг А’ не превосходит ранга А, так как ненулевой минор, входящий в А’, входит и в А.

15.Понятие 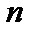-мерного арифметического вектора. Равенство векторов. Действия над векторами (сложение, вычитание, умножение на число, умножение на матрицу). Линейная комбинация векторов.

Упорядоченная совокупность n действительных или комплексных чисел 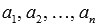называется n-мерным вектором.

Числа 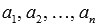называются координатами вектора.

Два (ненулевых) вектора a и b равны, если они равнонаправлены и имеют один и тот же модуль. Все нулевые векторы считаются равными. Во всех остальных случаях векторы не равны.

Сложение векторов. Для сложения векторов есть два способа.1. Правило параллелограмма. Чтобы сложить векторы 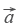и 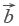, помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов 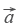и .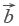

2. Второй способ сложения векторов — правило треугольника. Возьмем те же векторы 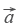и 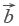. К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов 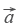и 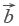. По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.

Вычитание векторов. Вектор 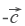направлен противоположно вектору 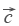. Длины векторов 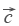и 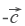равны. Теперь понятно, что такое вычитание векторов. Разность векторов 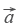и 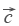— это сумма вектора 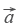и вектора .

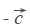Умножение вектора на число

При умножении вектора 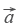на число k получается вектор, длина которого в k раз отличается от длины 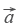. Он сонаправлен с вектором 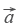, если k больше нуля, и направлен противоположно 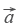, если k меньше нуля.

Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними. Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов 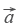и 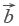.