Преобразование декартовых координат

Параллельный перенос СК

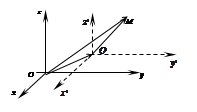Пусть , , , , ,

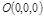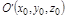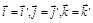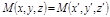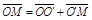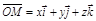, тогда ,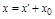
, ,
.

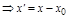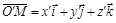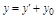
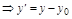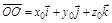
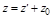
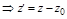Таким образом, в системе 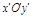координаты точки .

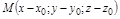Поворот СК на плоскости

Введем четыре СК: ,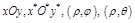

: .

: .

= = = .

= =
= .

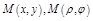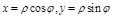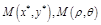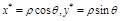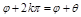
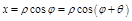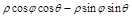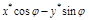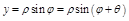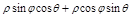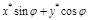§ 5. Приведение общего уравнения линии
2-го порядка к каноническому виду

Задача: по общему виду уравнения кривой 2-го порядка определить тип кривой и построить ее.

Будем рассматривать только случай, когда В=0, т.е. уравнение линии 2-го порядка имеет вид:

.

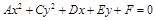Метод решения данной задачи – выделение полного квадрата: 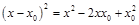(рабочая формула).

После выделения полного квадрата и перегруппировки слагаемых получим:

1) если 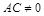, то ;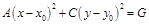

2) если 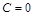, то ;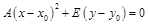

3) если 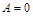, то .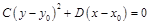

Сделаем параллельный перенос системы координат:

, .

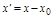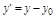В новой системе координат уравнение примет канонический вид. С учетом переноса СК, получим одну из следующих кривых:

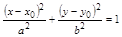– эллипс;

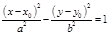–гипербола;

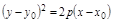– парабола;

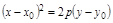– парабола.

ПР. 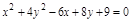. (эл.)

Плоскость.

Общее уравнение плоскости

В ДПСК в пространстве плоскость 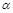задается уравнением 1-й степени:

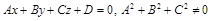. (13)

Опр. Вектор, перпендикулярный плоскости, называется ее нормалью.

Нетрудно установить (см. §1, п.1), что вектор 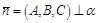. Таким образом, геометрический смысл коэффициентов общего уравнения плоскости состоит в том, что они дают координаты нормали плоскости.

Проведем анализ общего уравнения плоскости (13).

Если 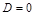, то плоскость 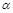проходит через начало координат: .

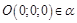Если 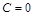, то 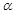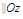, т.к. .

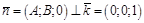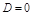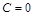Если и , то 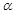содержит ось Oz.

Если A=0, B=0, то .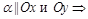

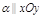Если A=0, B=0, 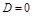, т.е. : .

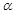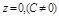
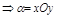Остальные случаи рассмотрите самостоятельно.

2. Уравнение плоскости в «отрезках»

Пусть в уравнении (13) 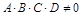. Разделим обе части уравнения на (–D), получим

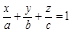, (14)

где 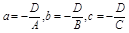− это отрезки, отсекаемые плоскостью на осях координат. Уравнение (14) называется уравнением плоскости в «отрезках».

Пр. 6x-4y+3z-12=0.

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Даны точка 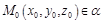и вектор 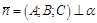. Составим уравнение плоскости .

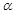Пусть точка 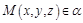. Тогда 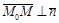. Следовательно, 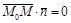. Получаем уравнение плоскости :

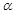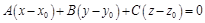. (15)

ПР.Найти уравнение плоскости 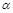, проходящей через 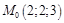перпендикулярно вектору .

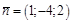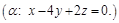
4. Уравнение плоскости, проходящей
через три данные точки

Пусть заданы три точки 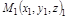, , 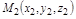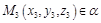. Составим уравнение плоскости .

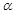Пусть точка 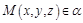. Тогда 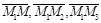компланарны. Следовательно, их смешанное произведение равно нулю: ( 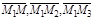)=0. Получаем:

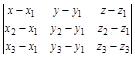=0. (16)

Замечание. Если точки 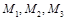лежат на одной прямой, то векторное произведение 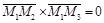. Тогда уравнение (16) справедливо для любой точки М. Это означает, что через любую точку пространства проходит плоскость, содержащая точки .

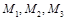ПР. Составить уравнение плоскости, проходящей через точки: , .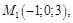

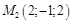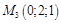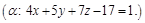
Угол между плоскостями

Опр. Углом между плоскостями называется меньший из двугранных углов, образованных этими плоскостями.

Пусть две плоскости заданы своими общими уравнениями:

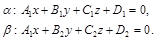
Найдем угол между ними.

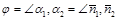или 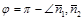. Следовательно,

.

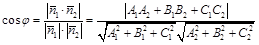Условие параллельности плоскостей:

.

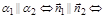
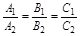Условие перпендикулярности плоскостей:

.

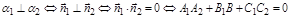ПР. Найти угол между плоскостями 5x-2y+z+2=0 и x+3z+3=0.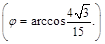

Прямая в пространстве.

Общие уравнения прямой.

Прямую в пространстве понимают как линию пересечения двух плоскостей: 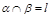. Поэтому общими уравнениями прямой в пространстве называют уравнения

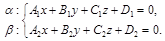(17)