Применение скалярного произведения в экономических задачах
Пример 1.Дана таблица объёма продаж фирмы (Рис. 23). Подсчитать объёмы прибыли фирмы.
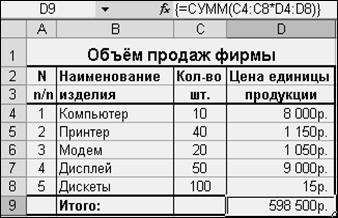 Выполнение:
Выполнение:
1.Объёмы прибыли фирмы
(общая стоимость всех изделий)
вычисляются по формуле
скалярного произведения векторов:
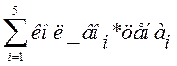 , где
, где
кол_во - вектор значений объёма продаж;
цена - вектор значений цены Рис.23. Таблица объёма продаж фирмы
изделия.
2.Ввести формулу массива в ячейку D9: {= СУММ(С4:С8* D4:D8)}
(или {= СУММ(кол_во* цена)});
Пример 2.Дана таблица реализации печатной продукции:
| N книг | Количество, шт. | Цена за ед. продукции, руб. | ||||
| n/n | январь | февраль | март | январь | февраль | март |
Подсчитать прибыль за квартал.
Выполнение:
1.Формула вычисления:
Прибыль за квартал = 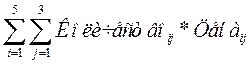 , где
, где
i - n/n автора и книги, j - номер месяца,
Количество – матрица значений количества проданной продукции
за 3 месяца;
Цена – матрица значений цены проданной продукции за 3 месяца.
2.Ввести формулу массива: {=СУММ(Кол_во*Цена)} в ячейку результата.
3.Проверить результат другим способом:
- добавить в таблицу столбец "Стоимость";
- поместить в этот столбец результат скалярного произведения вектора"Количество" и вектора "Цена" для каждой книги
- найти общую стоимость всех книг автосуммированием.
Сравнить результаты обоих способов.
6.5.2. Варианты заданий «Вычисление скалярного произведения векторов»
Вычислить скалярное произведение, если 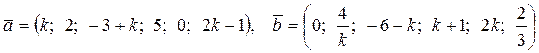 ,
,
где k – номер варианта задания.
| № | Задание | № | Задание |
| 1. | 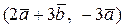 | 16. | 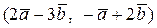 |
| 2. | 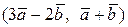 | 17. | 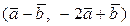 |
| 3. | 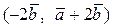 | 18. | 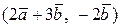 |
| 4. | 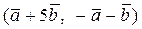 | 19. | 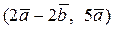 |
| 5. | 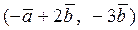 | 20. | 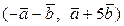 |
| 6. | 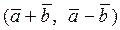 | 21. | 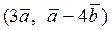 |
| 7. | 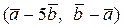 | 22. | 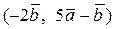 |
| 8. | 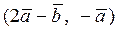 | 23. | 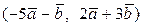 |
| 9. | 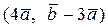 | 24. | 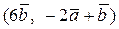 |
| 10. | 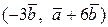 | 25. | 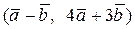 |
| 11. | 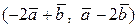 | 26. | 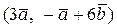 |
| 12. | 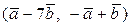 | 27. | 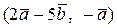 |
| 13. | 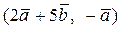 | 28. | 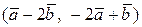 |
| 14. | 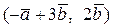 | 29. | 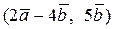 |
| 15. | 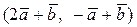 | 30. | 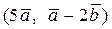 |
6.5.3. Варианты заданий: «Решение системы линейных уравнений методом обратной матрицы»
| № | задание | № | задание | № | задание |
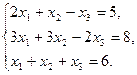 | 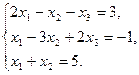 | 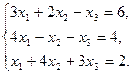 | |||
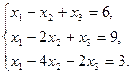 | 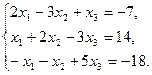 | 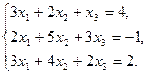 | |||
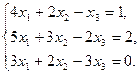 | 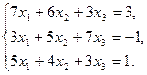 | 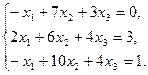 | |||
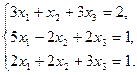 | 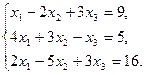 | 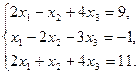 | |||
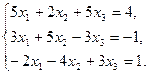 | 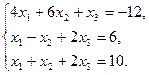 | 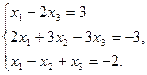 | |||
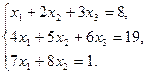 | 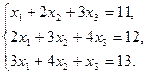 | 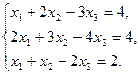 | |||
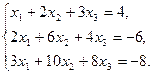 | 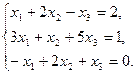 | 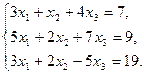 | |||
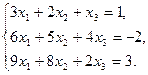 | 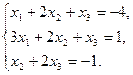 | 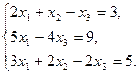 | |||
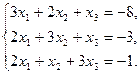 | 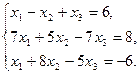 | 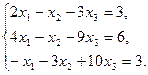 | |||
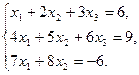 | 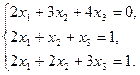 | 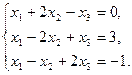 |
6.5.4. Варианты заданий: «Вычисление матричных выражений»
Выполнить операции над матрицами:
1. 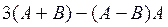 , где
, где 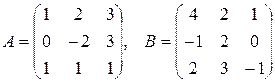 .
.
2. 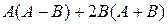 , где
, где 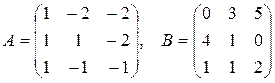 .
.
3. 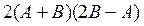 , где
, где 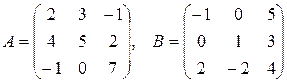 .
.
4. 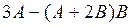 , где
, где 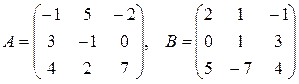 .
.
5. 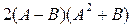 , где
, где 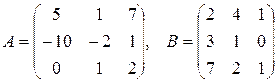 .
.
6. 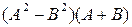 , где
, где 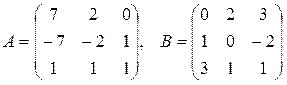 .
.
7. 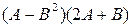 , где
, где 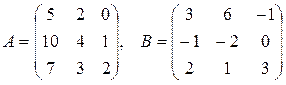 .
.
8. 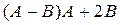 , где
, где 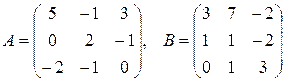 .
.
9. 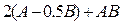 , где
, где 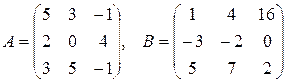 .
.
10. 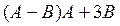 , где
, где 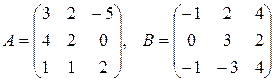 .
.
-
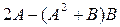 , где
, где 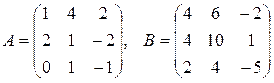 .
.
12. 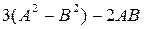 , где
, где 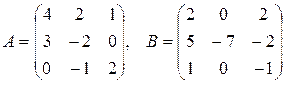 .
.
13. 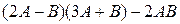 , где
, где 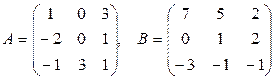 .
.
14. 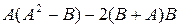 , где
, где 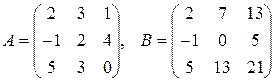 .
.
15. 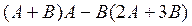 , где
, где 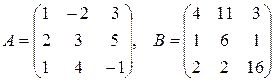 .
.
16. 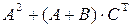 , где
, где 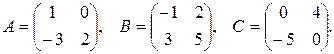
17. 3А3-А2+2Е, где 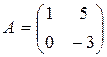 .
.
18. 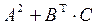 , где
, где 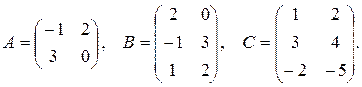
19. 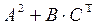 , где
, где 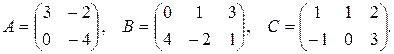
20. 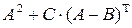 , где
, где 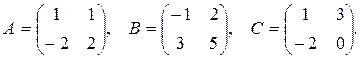
21. 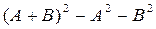 , где
, где 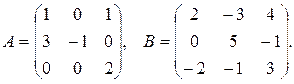
22. 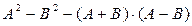 , где
, где 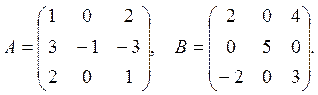
-
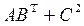 , где
, где 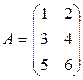 ,
, 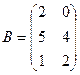 ,
, 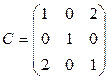 .
.
24. ABC-3Е, где 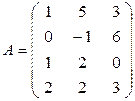 ,
, 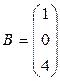 , C = (-1 6 10 5).
, C = (-1 6 10 5).
25. АТ·В-5С, где 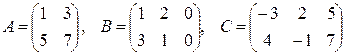
26. 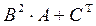 , где
, где 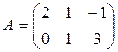 ,
, 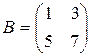 ,
, 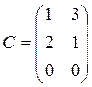 .
.
27. 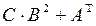 , где
, где 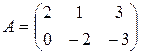 ,
, 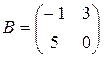 ,
, 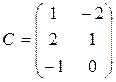 .
.
28. 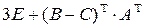 , где
, где 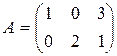 ,
, 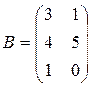 ,
, 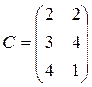 .
.
- А·АТ·А-В Т, где А = (1 0 –2 3),
 .
. -
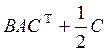 , где
, где 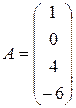 , B = ( 2 -1 3 5 ), C = ( 7 ).
, B = ( 2 -1 3 5 ), C = ( 7 ).
GПримечание. Е –единичная матрица соответствующего порядка.
7. Лабораторная работа по теме: «Финансовые функции»
Цель работы: знакомство с функциями Excel, предназначенными для
финансовых расчетов.
Изучение большинства дисциплин, использующих финансовые расчёты, происходит на старших курсах, потому в рамках дисциплины «Информатика» на 1 курсе рассматриваются самые простые финансовые расчёты и функции Excel. Поскольку аргументы финансовых функций являются типовыми, то подробное изучение хотя бы одной функции позволит в будущем правильно применять и другие финансовые функции Excel в расчётах.
Теоретическая справка. Подробную информацию по данной теме можно получить в [1] (п.7 «Финансовые функции»).
В данной лабораторной работе в качестве примера используется функция БС[1] (Категория†Финансовые) – будущая стоимость инвестиций на основе периодических постоянных (равных по величине сумм) платежей и постоянной процентной ставки.
Функция БСприменяется для расчётов по кредитованию и ожидаемых сумм по вкладам.Эти суммы вычисляются, как правило, по схеме простых и сложных процентов, т.е. базовая сумма (Р) возрастает за определённый период (t) на сумму, рассчитанную за проценты (I) и становится равнойS = Р + I(простые проценты),затем на следующий период tбазовая сумма (S) снова возрастает на сумму по процентам и т.д. Говорят, что сложные проценты рассчитываются на последовательно изменяющуюся базу (базовую сумму), «проценты на проценты».
Начисление по схеме простых процентов (постоянная база): S+P(1+rt)=0,
Начисление по схеме сложных процентов (функция БС): S + Р(1 + r)t = 0 ,где r = 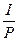 - процентная ставка за период (ден.ед./год).
- процентная ставка за период (ден.ед./год).
Форма записи функции БС имеет следующий вид:
БС(Ставка, Кпер, Плт, Пс, Тип),
где:Ставка – процентная ставка за период.
Кпер – общее число периодов выплат инвестиции.
Плт – выплата, производимая в каждый период и не меняющаяся за все время выплаты.
Пс – общая сумма, которая на настоящий момент равноценна серии будущих выплат.
Тип– значение 0 или 1, обозначающее, должна ли производиться выплата в начале периода (1) или же в конце периода (0 или отсутствие значения).
Пример 1. По вкладу размером 2000 тыс. руб. начисляется 10% годовых. Рассчитать, какая сумма будет на сберегательном счете через 5 лет, если проценты начисляются ежемесячно.
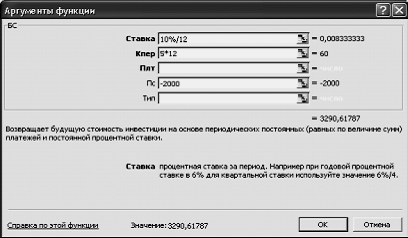 Решение:
Решение:
БС(10%/12;5*12;;-2000)
GПримечания.
1. Годовая процентная ставка делится на 12, т. к. начисление производится ежемесячно.
2. Положительные платежи означают поступление денег, отрицательные платежи - выплату денег
(-2000).
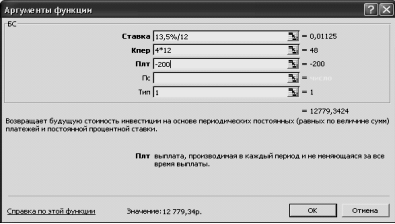 Пример 2. На сберегательный счет вносятся платежи по 200 тыс. руб. в начале каждого месяца. Рассчитать, какая сумма окажется на счете через 4 года при ставке процента 13,5 годовых.
Пример 2. На сберегательный счет вносятся платежи по 200 тыс. руб. в начале каждого месяца. Рассчитать, какая сумма окажется на счете через 4 года при ставке процента 13,5 годовых.
Решение:
=БС(13,5%/12;4*12;-200;;1)
GПримечание.
1. Одинаковые суммы вносятся периодически, потому заполняется аргумент Плт ;
2. Платежи выполняются в начале месяца:Тип=1
7.1.1. Варианты заданий «Простые и сложные проценты»
1.Банк 15.01.03 выдал фирме кредит в размере 500000 руб. для завершения строительных работ. Кредит выдан до 15.03.03 под 110% годовых. Рассчитать возвратную сумму для банка.
2.Банк дает ссуду 100000 руб. на полтора года под годовую процентную ставку 16% с ежеквартальным начислением. Определить конечную сумму платежа.
3.Банк принимает вклад 100000 руб. на срок 3 месяца с объявленной годовой ставкой 905 или на 6 месяцев под 100%. Как выгоднее вкладывать деньги на полгода: дважды на три месяца или один раз на 6 месяцев?
4.Какова сумма долга через 28 месяцев, если его первоначальная величина 100000 руб., проценты сложные, ставка 25%, начисление поквартальное?
5.Фермер взял льготный кредит в одном из частных банков 25000 руб. сроком на 5 лет под 3 простых процента. Определить, какую сумму должен возвратить фермер частному банку через 5 лет?
6.Для покупки квартиры взята ссуда 1000000 руб. на 2 года под ставку 24% годовых с ежеквартальным начислением. Определить возвратную сумму.
7.Банк выдает ссуду в размере 50000 руб. на 6 месяцев с годовой ставкой 120% или на год с годовой ставкой 140%. Как выгоднее получить ссуду: дважды по 6 месяцев или 1 раз в год?
8.Определить конечную сумму вклада в 1000 руб. через 2, 3, 4, 5, 6 лет при годовых процентных ставках 5, 10, 15, 20 и 30%?
9.Вы открываете счет и собираетесь вкладывать по 1400 руб. в начале каждого года в течение 8 лет при годовой ставке 3,5%. Сколько денег будет на счете через 8 лет?
10.Вы открываете счет и собираетесь вкладывать по 400 руб. в начале каждого месяца в течение 5 лет при годовой ставке 3%. Сколько денег будет на счете через 5 лет?
11.Какова сумма долга через 26 месяцев, если его первоначальная величина 500000 руб., проценты сложные, ставка – 20% годовых, начисление поквартальное?
12.По вкладу размером 3000 тыс. руб. начисляется 13% годовых. Рассчитать, какая сумма будет на счете через 4 года, если проценты начисляются ежемесячно.
13.Вкладчик открывает счет и планирует вносить на счет 2000 руб. в начале каждого месяца, ставка – 11% годовых. Какая сумма будет на счете через 5 лет?
14.Вкладчик открывает счет и планирует вносить на счет 2000 руб. в начале каждого месяца, ставка – 11% годовых. Какая сумма будет на счете через 5 лет, если счет был открыт 3 года назад и на настоящий момент на нем 10000 руб.?
15.Вложены деньги в банк в сумме 20 млн. руб. на 3 года под 20% годовых. Какую схему начисления сложных процентов: один раз в год, раз в полугодие, раз в квартал, раз в месяц или ежедневно - выберет вкладчик?
16.Стоимость земли, купленной за $20000, повышается на 15% в год (по сложному проценту). Сколько она будет стоить через 5 лет без учета налогов, страховых сборов и торговых расходов?
17.Ссуда в размере 10 млн. руб. выдана 20 января 2005г до 5 октября 2005г под 18%, проценты простые. Подсчитать, какую сумму должен заплатить должник.
18.Банк предлагает два варианта вложений денежных средств:
а) на срок 1 месяц — 22 % годовых,
б) на срок 6 месяцев — 23 % годовых.
Определить наиболее выгодную схему длительной финансовой операции для вкладчика, располагающего суммой 10000 руб.
19.Платежи величиной 5000 руб. вносятся ежегодно в течение 5 лет с начислением на них процентов по сложной ставке 15% годовых. Определить наращенную сумму.
20.Вкладчик намерен внести 40 тыс. руб. на один год в банк, который гарантирует выплату 12 сложных процентов годовых с ежемесячным начислением. Рассчитать будущий размер вклада.
21.Стоимость обучения в ВУЗе за 1-ый, 2-ой, 3-ий, 4-ый и 5-ый курсы составляет 15, 16, 17, 18, 19 тыс. руб. соответственно. Абитуриент вложил за 1 год до поступления в ВУЗ 45000 руб. в банк, обеспечивающий выплату 18% годовых. Сможет ли он покрыть все расходы на обучение?
22.Вас просят дать в долг 210000 руб. и обещают возвращать по 31000 руб. ежегодно в течение 7 лет. Определить, выгодна ли сделка (с точки зрения размера получаемой в конце срока суммы), если эту же сумму вы можете положить в банк под 10% годовых.
23.По вкладу размером 3500 тыс. руб. начисляется 13% годовых. Рассчитать какая сумма будет на сберегательном счете через 4 года, если проценты начисляются ежемесячно.
24.По вкладу размером 7500 тыс. руб. начисляется 13% годовых. Рассчитать какая сумма будет на сберегательном счете через 3 года, если проценты начисляются поквартально
25.Выдан кредит в размере 2 млн. долл. С 12.01.2005 по 22.06.2005 под 25% годовых. Рассчитать сумму погасительного платежа.
26.Сумма 1600 руб. размещена под 8% годовых на 8 лет. Проценты начисляются раз в квартал. Какая сумма будет на счете?
27.Банковская процентная ставка составляет 15% годовых. Рассчитать сумму вклада через 5 лет, если первоначальный вклад составлял 100 тыс. руб.
a) применяя формулу простых процентов;
b) применяя формулу сложных процентов (% начисляются 1 раз в год);
c) применяя формулу сложных процентов (% начисляются 1 раз в квартал);
d) применяя формулу сложных процентов (% начисляются 1 раз в месяц);
e) применяя формулу сложных процентов (% начисляются каждый день);
28.Банки А и Б предлагают вкладчикам 8% годовых. При этом банк А начисляет 8% по простой процентной ставке, банк Б - по сложной процентной ставке раз в полгода. Определить, какой из банков предлагает более выгодные условия вкладчику, делающему вклад на 6 месяцев и на 12 месяцев.
29.Банк предлагает компании ссуду на приобретение новой техники в размере 40000 руб. какую сумму придется вернуть банку по истечении срока ссуды, если она предоставляется на три месяца под 14% годовых по схеме простых процентов?
30.Вкладчик открывает счет и планирует вносить на счет 6000 руб. в начале каждого месяца, ставка – 11% годовых. Какая сумма будет на счете через 5 лет, если счет был открыт 3 года назад и на настоящий момент на нем 10000 руб.?
Контрольные вопросы
1. Что такое электронная таблица? Чем она отличается от обычной таблицы?
2. Какую структуру имеет строка формул?
3. Как задается адрес ячейки? Что понимается под координатами ячейки?
4. Для чего нужен маркер заполнения текущей ячейки?
5. Что может находиться в ячейке Excel?
6. Что понимается под форматом ячейки?
7. Какие типы данных можно вводить в ячейки листа?
8. Что происходит, если введенное значение не помещается в ячейку?
9. Описать способы редактирования данных в ячейках.
10. Когда следует применять команду Специальная вставка?
11. Сформулировать правила записи формул в Excel.
12. Описать порядок работы с Мастером функций.
13. Какие аргументы могут иметь функции в Excel?
14. Как включить функцию в формулу?
15. Что означает метод последовательной детализации при вычислениях?
16. Ошибочные значения в Excel?
17. Перечислить несколько статистических функций Excel.
18. Перечислить логические функции Excel.
19. Перечислить аргументы функции ЕСЛИ.
20. Алгоритм какого типа позволяет реализовать функция ЕСЛИ?
21. Чем отличаются функции СЧЕТ и СЧЕТЗ?
22. Описать назначение функций СУММЕСЛИ и СЧЕТЕСЛИ.
23. Какие типы адресации ячеек существуют?
24. Какой тип адресации ячеек устанавливается Excel по умолчанию?
25. Для чего необходимо изменять тип адресации? Какой клавишей?
26. Каким образом изменяется относительный адрес при копировании формулы?
27. Какой тип адреса имеет именованная ячейка?
28. Как с помощью адресации рассчитать таблицу значений функции двух переменных?
29. Что является основой диаграммы?
30. Описать порядок создания диаграмм в Excel.
31. Перечислить основные типы и элементы диаграмм в Excel.
32. Каким образом можно добавить новые данные к существующей диаграмме?
33. В каких задачах используется табулирование функции?
34. Для каких задач можно использовать команду Подбор параметра?
35. Что называют табличной формулой, ее особенности, назначение?
36. Какие задачи матричной алгебры можно решить средствами Excel?
37. Как используется скалярное произведение в экономических задачах?
38. Для чего предназначена функция БС? Как её применять?
9. 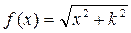 Контрольные задания
Контрольные задания
1.Рассчитать таблицу значений функции: , где x меняется от 2 до -2, количество значений х: 10; k – параметр, задаваемый пользователем таблицы. Построить график функции. Задавая различные значения параметра, проследить за изменениями графика.
2.Рассчитать таблицу значений функции f(x)=cos(kx+b) на некотором отрезке области определения, k, b – параметры, задаваемые пользователем таблицы. Построить график функции. Задавая различные значения параметров, проследить за изменениями графика.
3. 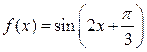
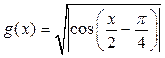 Рассчитать таблицу значений функций: где х изменяется от 2 до 4, и
Рассчитать таблицу значений функций: где х изменяется от 2 до 4, и
количество значений х: 10;.
Построить графики этих функций на одной координатной плоскости. Найти координаты точек пересечения функций.
4.Оклад работников организаций бюджетной сферы определяется по Единой тарифной сетке (ЕТС) следующим образом. Каждому работнику присваивается разряд от 1-го до 18-го, а для каждого разряда устанавливается коэффициент, по которому определяется оклад работника данного разряда путем умножения коэффициента на минимальный размер оплаты труда (МРОТ). Рассчитать оклад работника каждого разряда.
Так как величина МРОТ периодически меняется правительством, то ее целесообразно записать один раз в отдельной ячейке вне таблицы. Построить диаграмму значений коэффициента по разрядам ЕТС.
| Разряд ЕТС | Коэффициент | Оклад | Разряд ЕТС | Коэффициент | Оклад |
| 2,44 | |||||
| 1,11 | 2,68 | ||||
| 1,23 | 2,89 | ||||
| 1,36 | 3,12 | ||||
| 1,51 | 3,36 | ||||
| 1,67 | 3,62 | ||||
| 1,84 | 3,9 | ||||
| 2,02 | 4,2 | ||||
| 2,22 | 4,5 |
5.Подготовить лист для расчета суммы денег, выплачиваемой каждому из сотрудников. В него включить сведения: Ф.И.О. сотрудника, оклад, подоходный налог, пенсионный налог, профсоюзный взнос, сумму к выплате.
Сколько сотрудников получили зарплату более 2000 руб.?
Подоходный налог вычисляется по формуле: 13% от оклада за вычетом минимального размера оплаты труда (МРОТ) и пенсионного налога. Пенсионный налог и профсоюзный взнос составляют по 1% от оклада. Так как МРОТ и проценты налогов периодически меняются, то их величины целесообразно записать один раз, в отдельные ячейки вне таблицы.
Построить диаграмму выплат каждому сотруднику.
6.Фирма состоит из двух отделений, суммарная величина прибыли которых в минувшем году составила 12 млн. у. е. На этот год запланировано увеличение прибыли первого отделения на 70%, второго – на 40%. В результате суммарная прибыль должна вырасти в 1,5 раза. Какова величина прибыли каждого из отделений: а) в минувшем году; б) в этом году?
Составить систему уравнений и решить с помощью формул массива.
7.Фирмой было выделено 236 тыс. у. е. для покупки 29 предметов для оборудования офиса: несколько компьютеров по цене 20 тыс. у. е. за компьютер, офисных столов по 8,5 тыс. у. е. за стол, стульев по 1,5 тыс. у. е. за стул. Позже выяснилось, что в другом месте компьютеры можно приобрести по 19,5 тыс. у. е., а столы – по 8 тыс. у. е. (стулья по той же цене), благодаря чему на ту же сумму было куплено на 1 стол больше. Выяснить, какое количество единиц каждого вида оборудования было приобретено. Составить систему уравнений и решить с помощьюформул массива.
8.Подсчитать общую стоимость всех путевок, а также продажи в каждую страну. Вычисления выполнять по формулам массива. Перевести цену путёвок из руб. в € по принятому курсу. Построить диаграмму продаж в каждую страну.
| Страна | Количество | Цена за 1 путёвку | Общие продажи, р. | Общие продажи,€ | |||||
| июнь | июль | август | июнь | июль | август | ||||
| Турция | |||||||||
| Италия | Общая формула: | ||||||||
| Греция | |||||||||
| Итого - |
9.Таблица содержит сведения о работе салона проката видеокассет: фамилия клиента, название фильма, дата выдачи, срок проката (в днях). Для каждого клиента определить срок возврата и стоимость проката, зная цену проката за одну штуку (в день). Вычислить истек ли срок проката каждого клиента на текущую дату. Сколько клиентов просрочили возврат видеокассет. Построить диаграмму стоимости проката видеокассет для каждого клиента.
10.В таблице содержится следующая информация о продовольственных товарах: наименование товара, дата изготовления, срок годности (в днях), цена за ед. продукции, остаток на складе (в ед.). Необходимо определить стоимость остатка каждой партии товара; установить, истек ли срок годности на заданную (текущую) дату; также вычислить суммарную стоимость просроченного товара. Построить диаграмму стоимости остатка каждой партии товара.
11.Таблица содержит данные о партиях лекарств: наименование лекарства, оптовая цена за ед., объем партии (в ед.), дата выпуска, срок годности (в годах). Необходимо для каждой партии определить, истек ли срок годности на заданную дату (истек / истекает менее, чем через месяц / не истек). Определить стоимость партий с неистекшим сроком, а для просроченных лекарств эту стоимость возвращать со знаком «-». Построить диаграмму оптовой цены каждого лекарства.
12.Таблица о почтовых посылках содержит следующую информацию: код посылки, категория срочности (срочная/обычная), категория ценности (ценная/обычная), масса (кг), оценочная стоимость (только для ценных посылок). Отдельно заданы стоимости доставки обычных и ценных посылок в расчете на 1 кг веса. Необходимо рассчитать полную стоимость доставки каждой посылки, учитывая, что наценка за срочность доставки для обычных посылок составляет 30%, а для ценных – 60%. Необходимо также подсчитать количество ценных посылок. Построить диаграмму полной стоимости доставки каждой посылки.
13.В таблице содержатся данные о результатах проверки измерительных приборов: инв. номер прибора, класс точности (1, 2), фактическая относительная погрешность (в %). В отдельных ячейках заданы величины максимально допустимой величины относительной погрешности для каждого класса точности. Требуется сделать заключение об исправности приборов (годен / не годен), оценив, превышает ли фактическая погрешность максимально допустимую для данного класса точности. Построить диаграмму фактической относительной погрешности каждого прибора.
14.В таблице содержится информация о музыкальных сборниках, выпускаемых на компакт-дисках в формате MP3: название сборника, дата выпуска, количество дисков в сборнике, вариант исполнения (обычный / подарочный). Отдельно заданы базовая цена сборника на одном диске; наценка за подарочный вариант исполнения. Необходимо сформировать продажную цену каждого сборника с учетом количества дисков (базовая цена умножается на количество дисков в комплекте) и варианта исполнения. Также нужно подсчитать количество сборников, выпущенных после заданной даты. Построить диаграмму продажной цены каждого сборника.
15.Известен прогноз погоды на ближайшую неделю, сведенный в таблицу:
| Дата | Средняя дневная температура, °С | Занятия |
| = СЕГОДНЯ()+1 | -35 | Отменены |
| … | … | … |
В отдельной ячейке задано предельное значение температуры. Необходимо в столбце «Занятия» вывести сведения (Отменены / Проводятся), в какие дни занятия в школах предположительно будут отменены; считать, что занятия не проводятся, если температура не выше предельной. Если дата соответствует выходному дню (воскресенье), то в столбце «Занятия» вывести значение «Выходной». Используя условное форматирование, отметить цветом ячейки (или строки), соответствующие дням, в которые занятия будут отменены. Определить количество рабочих дней с температурой не выше предельно допустимой. Построить диаграмму ежедневной температуры.
16.Результаты тестирования абитуриентов при поступлении в вуз определяются так: свыше 90% правильных ответов - 5 баллов, от 75% до 90% - 4; от 60% до 75% -3. Рассчитать и ввести необходимые данные.
Подсчитать, сколько абитуриентов поступило в вуз и сколько не поступило.
Построить диаграмму полученных баллов по каждым абитуриентом.
Сумма проходных баллов = 8
| абитуриент | Тест по математике | Оценка по математике | Тест по физике | Оценка по физике | Баллы | Поступил (да/нет) |
| Иванов | 92% | 81% | ||||
| Петров | 85% | 78% | ||||
| Сидоров | 72% | 66% |
17.В таблице содержатся сведения о библиотечных книгах, находящихся на руках у читателей: название, автор, категория (худ. книга, учебник, учебное пособие), фамилия читателя, дата выдачи, срок возврата (в сутках). Определить, истек ли срок возврата для каждой взятой книги на заданную дату (текущую дату). Подсчитать количество просроченных учебников. Подсчитать для каждой просроченной книги стоимость штрафа, исходя из следующего: для учебников и учебных пособий каждые лишние сутки взимается 3 руб, а для худ. книг – 2 руб. Построить диаграмму срока возврата каждой книги.
18.Таблица содержит информацию о заказах на фотопечать: фамилия клиента, формат фотографий (10х15, 15х21, 30х40), количество фотографий, тип поверхности фотобумаги (матовая, глянцевая), тип фотобумаги (обычная, металлизированная). Задана стоимость печати фотографии каждого формата на обычной бумаге. Печать фотографий с металлизированной подложкой дороже на 30%. Рассчитать стоимость печати для каждого заказа; определить, какую долю от общего объема заказов (в руб.) составляет печать на глянцевой бумаге. Определить количество заказов на печать на бумаге с металлизированной подложкой. Построить диаграмму стоимости печати каждого заказа.
19.В таблицу внесены данные об услугах, оказанных автовладельцам в автосервисе: фамилия И.О. автовладельца, марка автомобиля, наименование услуги, дата оказания услуги, стоимость услуги. Определить суммарную стоимость услуг, оказанных после определенной даты. Определить, какую долю от общего количества оказанных услуг составляет услуга «мойка». В отдельном столбце начислить размер скидки для всех услуг, кроме мойки. Скидки начисляются так: 2% для услуг, стоимость которых составляет от 100 до 2000 руб., 5% для услуг стоимостью свыше 2000 руб. Построить диаграмму скидок по каждой услуге.
20.В фирме принята следующая система стимуляции пунктуальности сотрудников: если количество опозданий за месяц не превышает двух, то сотрудник поощряется премиальной надбавкой; если сотрудник опаздывал на работу от 3 до 10 раз, он лишается надбавки; если же работник опаздывал более 10 раз за месяц, то он лишается надбавки, и дополнительно из его зарплаты вычитается 1% за каждое опоздание. В таблицу внесены данные: ФИО сотрудника, базовая зарплата, количество опозданий за месяц. Отдельно задана величина премиальной надбавки (в процентах от базовой зарплаты). Нужно рассчитать сумму зарплаты к выдаче для каждого сотрудника. Построить диаграмму зарплаты каждого сотрудника.
21.Таблица по учету произведенной рабочими продукции за месяц содержит следующие сведения: фамилия И.О. рабочего, разряд рабочего (от 3 до 6), количество произведенных деталей (шт.), количество бракованных деталей (шт.). Также заданы базовая ставка оклада (руб.), норма производства (шт.) Определить для каждого рабочего размер заработной платы, учитывая, что:
- зарплата включает постоянную часть (оклад), определяемую по формуле:
Окл = БазСтавка + (8 - Разряд) × 400;
- к постоянной части добавляется премиальная часть, составляющая 30% оклада, если норма производства выполнена, 50%, если норма производства выполнена более чем на 15%. Количество брака вычитается из общего количества произведенных деталей.
- из заработной платы вычитается штраф в размере 10% оклада, если доля брака составляет более 5% от общего количества произведенных деталей.
Построить диаграмму заработной платы каждого рабочего.
22.Таблица содержит данные о результатах контроля произведенных деталей: код детали, контролируемый размер детали (в мм), фамилия И.О. контролера. Также заданы: базовая величина размера (мм) детали, относительное предельное отклонение (в процентах) от базовой величины размера. Необходимо определить для каждой детали:
- является ли она годной (модуль разности фактической и базовой величин размера не должен превышать предельного отклонения в абсолютном выражении),
- исправимым браком (фактический размер больше предельно допустимого),
- неисправимым браком (фактический размер меньше предельно допустимого).
Определить количество годных деталей. Определить долю неисправимого брака от общего количества деталей. Сколько всего деталей проконтролировал Иванов И.П. Построить диаграмму размера каждой детали.
23.В таблице содержится информация о заказах билетов на авиарейсы авиакомпании (а/к) «Крылышки»: ФИО пассажира, порт прибытия, класс (эконом, туристический, бизнес), базовая цена (руб.), количество предыдущих поездок пассажира этой а/к. В отдельных ячейках заданы величина скидки (в % от базовой цены) и величина коммерческого сбора (в % от базовой цены). Необходимо определить полную стоимость билета следующим образом:
- к базовой цене прибавляется сумма коммерческого сбора;
- для различных классов установлены постоянные коэффициенты увеличения базовой цены: эконом - 1,0, туристический - 1,3, бизнес - 1,7;
- если количество предыдущих поездок пассажира не менее трех, то ему предоставляется скидка.
Определить количество пассажиров, заказавших билеты на рейсы а/к в первый раз. Построить диаграмму полной стоимости билета каждого пассажира.
24.В таблицу сведены данные о результатах тестирования ресурса картриджей для различных моделей струйных принтеров: модель принтера, цена принтера, цена картриджа, количество страниц, напечатанных с использованием одного картриджа, ресурс принтера (в страницах). Необходимо условно разделить принтеры на две группы (дорогой / недорогой) по удельной стоимости печати (в расчете на одну напечатанную страницу). Удельная стоимость печати определяется по формуле:
- УдСт = ЦенаПринтера / РесурсПринтера + ЦенаКартр / КолСтраниц.
- Если удельная стоимость превышает заданную отдельно пороговую величину, то принтер относится к дорогим, в противном случае – к недорогим.
Построить диаграмму удельной стоимости печати каждой модели принтера.
25.Имеется информация о любительских цифровых фотокамерах: модель, относительный размер матрицы, количество точек матрицы, цена, сведенная в таблицу:
| Модель | Кол-во точек матрицы, МПикс | Цена, руб. | Возможна печать фото 15х22 см |
| М1 | 3.0 | … | |
| М2 | 5.1 | ||
| М3 | 5.1 | ||
| М4 | 7.1 | ||
| М5 | 7.1 | ||
| М6 | 5.1 |
В отдельной ячейке задано потребное разрешение для печати (измеряется в dpi, точек на дюйм), которое может принимать значения: 150, 200, 300, 400 dpi.
Если потребное для печати число точек (пикселей), определяемое по формуле:
ПотребноеКолТочек = 15 × 22 / 2,542 ×Разрешение×2,
не будет превышать количества точек матрицы фотокамеры, то печать с заданным разрешением возможна («да»), в противном случае - «нет».
Определить также среднюю стоимость фотокамер с 5.1 Мпикс. матрицей.
Построить диаграмму стоимости каждой модели фотокамеры.
Литература
1. А.Н. Асанова. Вычисления в Excel. Методическое пособие /г. Наб.Челны: Камский издательский дом, 2001, 86с.
2. Л.В. Маликова, А.Н. Пылькин. Практический курс по электронным таблицам MS Excel: Учебное пособие для вузов.- М.: Горячая линия – Телеком, 2004. -224с.
3. С.М. Лавренов. Excel: Сборник примеров и задач. – М: Финансы и статистика, 2000. – 336с.
4. О.Н. Салманов. Математическая экономика с применением Mathcad и Excel. – СПб.: БХВ-Петербург, 2003.-464с.
5. Высшая математика для экономистов: учебник для вузов под ред. проф. Н.Ш. Кремера – М.: ЮНИТИ, 2001,- 471с.
[1] В версии Excel 2000 эта функция имеет имя БЗ (будущее значение) с теми же параметрами.
