Разностные уравнения второго порядка с постоянными коэффициентами

Рассмотрим однородное разностное уравнение второго порядка с постоянными коэффициентами

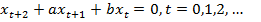. (11)

Будем искать его решения в виде 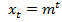, при этом 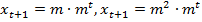. Подставляя найденные значения в (11), получаем уравнение

из которого, при 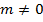, следует, что 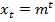является решением уравнения (11) тогда и только тогда, когда число 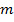является корнем характеристического уравнения

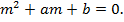(12)

Если 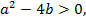то уравнение (12) имеет корни

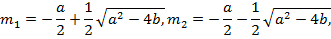
при этом общее решение уравнения (11) имеет вид

.

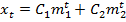Если 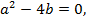то уравнение (12) имеет корень 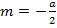кратности 2,

при этом общее решение уравнения (11) имеет вид

.

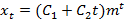Если 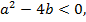то уравнение (12) имеет комплексно-сопряжённые корни, при этом общее решение уравнения (11) имеет вид

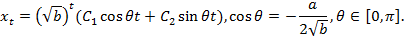
Во всех этих случаях при заданных значениях 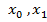можно найти 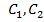, что однозначно определит решение уравнения (11).

Отметим, что в случае комплексно-сопряжённых корней характеристического уравнения имеет место осцилляция. При этом если 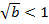, то колебания затухают, если 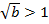, то их амплитуда растёт.

Примеры. Найти общее решение для каждого из уравнений

1.

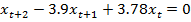
2.

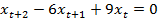
3.

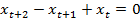
Первому уравнению соответствует характеристическое уравнение

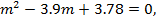
имеющее корни 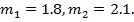Таким образом, общее решение этого уравнения имеет вид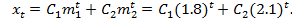

Второму уравнению соответствует характеристическое уравнение

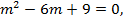
имеющее корень 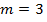кратности 2 и общее решение этого уравнения имеет вид .

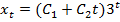Третьему уравнению соответствует характеристическое уравнение

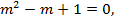
имеющее комплексно-сопряжённые корни .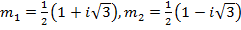

Для него 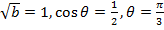и общее решение этого уравнения имеет вид

.

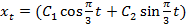Перейдём к неоднородному случаю и рассмотрим уравнение

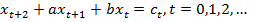. (13)

Как отмечалось выше, общее решение уравнения (12) имеет вид

+

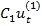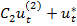
где 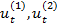- любые два линейно независимые решения (11), 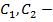произвольные постоянные, а 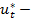любое частное решение уравнения (13).

В общем случае можно отыскать 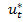по формуле (10), однако это требует большого количества вычислений. В ряде случаев можно заранее указать тот вид, в котором имеет смысл искать решение .

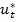Например, если 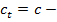постоянная и если 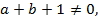то

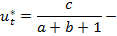
искомое частное решение. Если 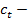линейная комбинация функций 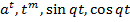, или их произведений, то можно использовать метод неопределённых коэффициентов, как в следующем примере.

Пример. Решить уравнение

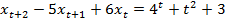
Общее решение соответствующего однородного уравнения имеет вид 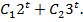Частное решение неоднородного уравнения ищем в виде

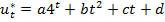, подставляя эту величину в исходное уравнение, получаем

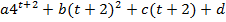-5(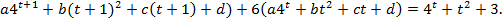

Ввиду линейной независимости функций 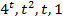из этого равенства вытекает, что 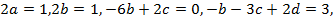откуда 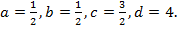Таким образом, общее решение этого уравнения имеет вид

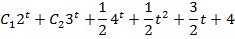
Задачи. Найти общее решение уравнения:

1.

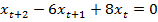
2.

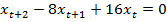
3.

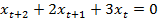
4.

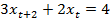
5.

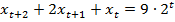
6.

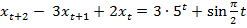
УСТОЙЧИВОСТЬ

Определение. Уравнение (13) называется глобально асимптотически устойчивым, если любое решение соответствующего уравнения (11) стремится к 0 при .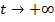

Теорема. Уравнение (13) является глобально асимптотически устойчивым, если модуль любого корня уравнения (12) меньше 1. Это условие можно равносильным образом выразить через коэффициенты уравнения (13):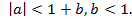

Пример. Уравнение 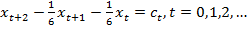является глобально асимптотически устойчивым.

Задачи . Исследовать глобальную асимптотическую устойчивость следующих уравнений:

1.

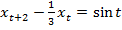
2.

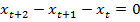
3. .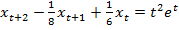