Свойства векторного произведения
1. При перестановке сомножителей векторное произведение меняет знак
.
2. Сочетательное свойство относительно скалярного множителя
.
3. Два ненулевых вектора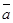 
и 
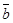коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору
.
4. Распределительное свойство
.
Пример 10.
Вычислить модуль векторного произведения векторов
и 
.
Решение:
По формуле 
получим
Тогда модуль векторного произведения равен 
.
Пример 11.
Найти площадь параллелограмма, построенного на векторах
и 
.
Решение:
Используя формулу 
получим
Пример 12.
Вычислить площадь треугольника ABC, если А(–2;1;3), В(2;–1;7),
С(11; 2; –5).
Решение:
Используя координаты вершин треугольника, находим
Тогда
=S
Пример 13.
Исследуйте векторы на коллинеарность
Решение:
Если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору)
а) Найдём векторное произведение
Таким образом, векторы 
и 
не коллинеарны.
б) Найдём векторное произведение
Значит, 
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Рассмотрим произведение векторов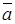 
, 
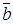и 
, составленное следующим образом 
.
Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешаннымпроизведением трех векторов. Смешанное произведение представляет собой некоторое число.
Свойства смешанного произведения
1. Смешанное произведение не меняется при перестановке сомножителей
.
2. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения
.
3. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей
.
4. Смешанное произведение ненулевых векторов 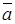, 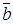и равно нулю тогда и только тогда, когда они компланарны.
Выясним геометрический смысл выражения 
. Построим параллелепипед, ребрами которого являются вектора 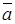, , 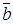и вектор 
(рис.9).
Рис. 9
Имеем
,
где S – площадь параллелограмма, построенного на векторах 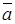и .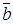
– для правой тройки векторов
– для левой тройки векторов;
где 
– высота параллелепипеда.
Получаем
.
Т.е. 
,
где V – объем параллелепипеда, образованного векторам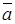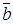и , и .
Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти вектора образуют правую тройку, и со знаком «минус», если они образуют левую тройку.
Объем параллелепипеда, построенного на векторах 
, 
вычисляется как
.
Объем треугольной пирамиды, построенной на этих же векторах, равен
.
Если 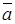, 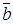и компланарны, то их смешанное произведение равно нулю.