Методика вычисления матрицы методом Зейделя
Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений
A∙X=B
с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду
X=B∙X+C
Здесь B – квадратная матрица с элементами bij (i, j = 1, 2, …, n), C – вектор-столбец с элементами cij (i = 1, 2, …, n).
В развернутой форме записи система имеет следующий вид:
x1 = b11x1 + b12x2 + b13x3 + … + b1nxn + c1
x2 = b21x1 + b22x2 + b23x3 + … + b2nxn + c2
. . . . . . . . . . . . . . . . .
xn = bn1x1 + bn2x2 + bn3x3 + … + bnnxn + cn
Операция приведения системы к виду, удобному для итераций, не является простой и требует специальных знаний, а также существенного использования специфики системы.
Самый простой способ приведения системы к виду, удобному для итераций, состоит в следующем. Из первого уравнения системы выразим неизвестное x1:
x1 = a11–1 (b1 – a12x2 – a13x3 – … – a1nxn),
из второго уравнения – неизвестное x2:
x2 = a21–1 (b2 – a22x2 – a23x3 – … – a2nxn),
и т. д. В результате получим систему
x1 =b12x2 + b13x3 + … + b1,n–1xn–1 +…+b1nxn+ c1 ,
x2 = b21x1 +…+b23x3 +… +b2,n–1xn–1 +…+b2nxn+c2 ,
x3 = b31x1 + b32x2 +… +b3,n–1xn–1 +…+b3nxn+c3 ,
. . . . . . . . . . . . . . . . . . . . . . .
xn = bn1x1 + bn2x2 + bn3x3 +… + bn,n–1xn–1 +cn ,
в которой на главной диагонали матрицы Bнаходятся нулевые элементы. Остальные элементы выражаются по формулам
bij = –aij / aii, ci = bi / aii (i, j = 1, 2, …, n, j ≠ i)
Конечно, для возможности выполнения указанного преобразования необходимо, чтобы диагональные элементы матрицы A были ненулевыми.
Описание метода. Введем нижнюю и верхнюю треугольные матрицы







 0 0 0 … 0 0 b12 b13 … b1n
0 0 0 … 0 0 b12 b13 … b1n
b21 0 0 … 0 0 0 b23 … b2n
B1 = b31 b32 0 … 0 , B2 = 0 0 0 … b3n
. . . . . . . . . . . . . . .



 bn1 bn2 bn3…0 0 0 0 … 0
bn1 bn2 bn3…0 0 0 0 … 0
Заметим, что B=B1+B2 и поэтому решение X исходной системы удовлетворяет равенству
X = B1∙X + B2∙X + C.
Выберем начальное приближение X(0) = [x1(0), x2(0), …, xn(0)]T. Подставляя его в правую часть равенства при верхней треугольной матрице B2и вычисляя полученное выражение, находим первое приближение
X(1) = B1∙X(0) + B2∙X(1)
Подставляя приближение X(1), получим
X(2) = B1∙X(1) + B2∙X(2)
Продолжая этот процесс далее, получим последовательность X(0), X(1), …, X(n), … приближений к вычисляемых по формуле
X(k+1) = B1(k+1) + B2(k) + C
или в развернутой форме записи
x1(k+1) = b12x2(k) + b13x2(k) + … + b1nxn(k) + c1 ,
x2(k+1) = b21x1(k+1) + b23x3(k) + … + b2nxn(k) + c2 ,
x3(k+1) = b31x1(k+1) + b32x2(k+1) + … + b3nxn(k) + c3 ,
. . . . . . . . . . . . . . . . . . . . . . . . . .
Xn(k+1) =bn1x1(k+1) +bn2x2(k+1) +bn3x3(k+1) +… +Cn .
|
|
|
|
|
|
(условие доминированния диагонали).
Метод Зейделя иногда называют также методом Гаусса-Зейделя, процессом Либмана, методом последовательных замещений.
Ручной счет
Исходные данные
| i | |||||
| Xi | -0,9 | -0,3 | 0,1 | 0,5 | 1,0 |
| Yi | -0,3 | 0,1 | 0,0 | 0,2 | 0,7 |
Ѱ1(X)=1, Ѱ 2(X)=X, Ѱ 3(X)=3X2-1
Система нормальных уравнений
Ѱ(Xi)=C1* Ѱ1(X)+C2* Ѱ2(X)+ C3* Ѱ3(X)
Ѱ(Xi)=C1*1+C2*X+C3*(3*X2-1)
|

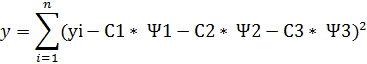
y`=0( min и max – точки экстремумы)
Условие минимума
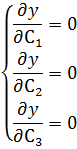
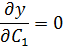
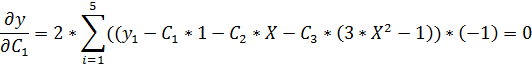
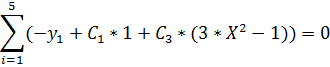
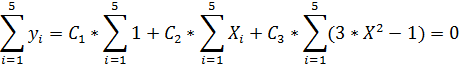
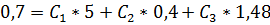 (1)
(1)
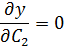
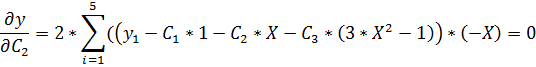
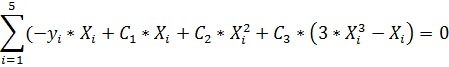
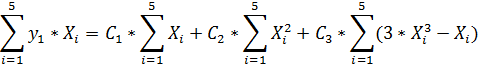
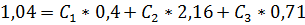 (2)
(2)
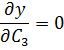
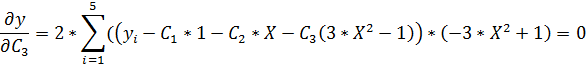
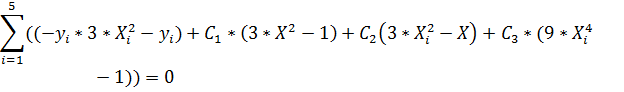
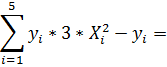
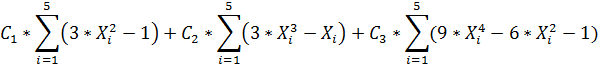
0,848= 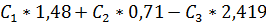 (3)
(3)