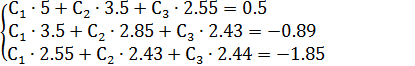Методика вычисления обратной матрицы

Один из методов решения системы линейных уравнений (3), записываемый в матричной форме А·Х=В, связан с использованием обратной матрицы А^-1. В этом случае решение системы уравнений получается в виде

Х=А^-1·В,

где А^-1–матрица, определяемая следующим образом.

Пусть А – квадратная матрица размером n х n с ненулевым определителем detA≠0. Тогда существует обратная матрица R=A^-1, определяемая условием A·R=E,

где Е – единичная матрица, все элементы главной диагонали которой равны I, а элементы вне этой диагонали – 0, Е=[E₁,..., E_n], где Е_i–вектор-столбец.

Матрица R –квадратная матрица размером n х n.

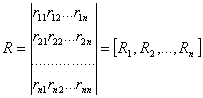
где Rj –вектор-столбец.

Рассмотрим ее первый столбец R=( r₁₁, r₂₁,…, r_n1)^T, где Т –означает транспонирование. Нетрудно проверить, что произведение A·R равно первому столбцу E₁=(1, 0, …, 0)^Т единичной матрицы Е, т.е. вектор R₁ можно рассмотреть как решение системы линейных уравнений A·R₁=E_1. Аналогично m –й столбец матрицы R , Rm, 1≤ m ≤ n, представляет собой решение уравнения A·Rm=Em, где Em=(0, …, 1, 0)^T m –й столбец единичной матрицы Е.

Таким образом, обратная матрица R представляет собой набор из решений n систем линейных уравнений

A·Rm=Em , 1≤ m ≤ n.

Для решения этих систем можно применять любые методы, разработанные для решения алгебраических уравнений. Однако метод Гаусса дает возможность решать все эти n систем одновременно, а независимо друг от друга. Действительно, все эти системы уравнений отличаются только правой частью, а все преобразования, которые проводятся в процессе прямого хода метода Гаусса, полностью определяются элементами матрицы коэффициентов (матрицы А). Следовательно, в схемах алгоритмов изменению подлежат только блоки, связанные с преобразованием вектора В. В нашем случае одновременно будут преобразовываться n векторов Em, 1≤ m ≤ n. Результатом решения также будет не один вектор, а n векторов Rm, 1≤ m ≤ n.

Ручной счет

3.1 Исходные данные.
Исходные данные заданы в виде табличной зависимости:

№
Xi	0.00	0.79	1.57	2.36	3.14
Yi	3.0	5.0	2.0	0.0	-2.0

φ₁(x) = 1
φ₂(x) = sin(x)
φ₃(x) = cos(x)

Метод MINU

Система нормальных уравнений

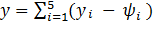²

Ψ(x) = C₁·1 + C₂·sin(x) + C₃·cos(x)

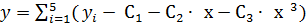²

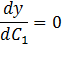
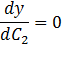
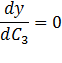
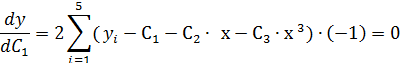
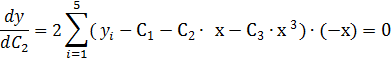
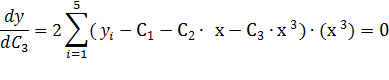
C₁:

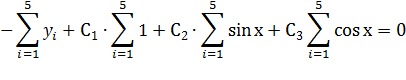
C₂:

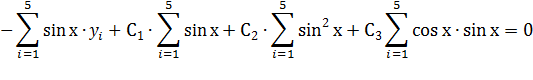
C₃:

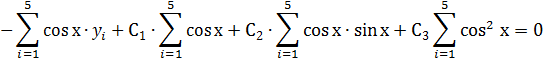Далее аппроксимируем функцию 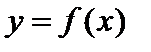. Для определения коэффициентов С₁, С₂ и С₃ воспользуемся системой:

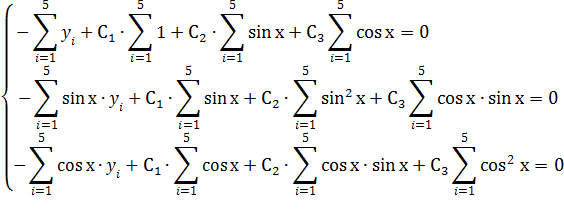
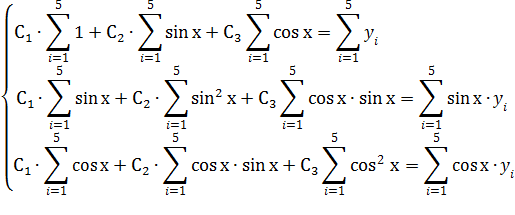
Таблица промежуточных вычислений:

	Xi	Yi	sin(xi)	cos(xi)	sin2(xi)	cos2(xi)	cos(xi) sin(xi)
	0.0
	0.79		0.710	0.703	0.504	0.4942	0.4993
	1.57		0.999		0.998
	2.36		0.704	-0.709	0.496	0.502	-0.4994
	3.14	-2	0.001	-0.999	0.0	0.998	-0.0009
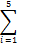	7.86		2.415	-0.005	1.999	1.994	-0.0001

Далее, используя итоговые суммы «Таблицы промежуточных вычислений» запишем систему в виде: