Основные свойства гиперболического тангенса
Показательные и логарифмические выражения
Показательная функция, гиперболические функции
Показательной функциейназывается функция
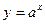,где 
.
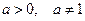Основные свойства показательной функции.
1. Область определения: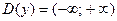 
.
2. Множество значений: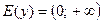 
.
3. Четность и нечетность: не обладает свойством четности.
4. Периодичность: не периодическая.
5. Нули функции: нулей не имеет.
6. Промежутки знакопостоянства:функция положительна для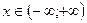 
.
7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.
8. Промежутки возрастания и убывания: если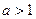 
функция возрастает для всех 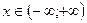; если 
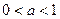–убывает для .
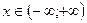9. Точки пересечения с осями координат: пересекает ось Оу в точке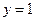 
, ось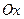 
не пересекает.
10. Асимптоты: прямая y = 0 (ось 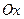) является горизонтальной асимптотой.
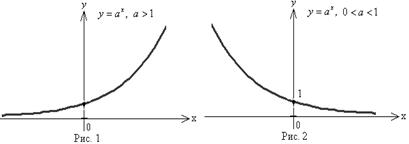
11. График функции дляa > 1 изображен на рисунке 1, для –на рис. 2.
Из свойств функции следует: неравенство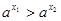 
равносильно неравенству:
1) 
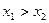, если ,
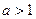2) 
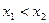, если .
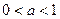Показательная функция с основанием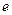 
, где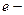 
иррациональное число 
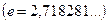, называется экспонентой, пишут 
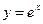или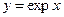 
.
Через показательные выражения с основанием 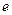определяются гиперболические функции.
Гиперболическим синусом называется функция
.
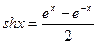Основные свойства гиперболического синуса.
1. Область определения: .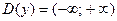
2. Множество значений: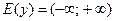 
.
3. Четность и нечетность: нечётная.
4. Периодичность: не периодическая.
5. Нули функции: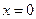 
.
6. Промежутки знакопостоянства:функция отрицательна для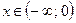 
, положительна – для 
.
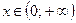7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.
8. Промежутки возрастания и убывания: функция возрастает для всех .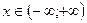
9. Точки пересечения с осями координат: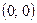 
.
10. Асимптоты: асимптот не имеет.
11. График функции изображен на рисунке 3.
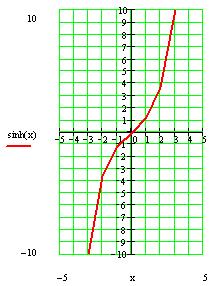
Рис. 3.
Гиперболическим косинусом называется функция
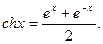
Основные свойства гиперболического косинуса.
1. Область определения: .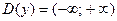
2. Множество значений: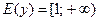 
.
3. Четность и нечетность: чётная.
4. Периодичность: не периодическая.
5. Нули функции: нулей не имеет.
6. Промежутки знакопостоянства:функция положительна для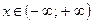 
.
7. Наибольшее и наименьшее значения: наименьшее значение, равное 1, функция принимает при .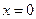
8. Промежутки возрастания и убывания: функция убывает при 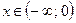; возрастает – при .
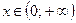9. Точки пересечения с осями координат: пересекает ось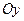 
в точке 
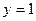, ось 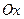не пересекает.
10. Асимптоты: асимптот не имеет.
11. График функции изображен на рисунке 4.
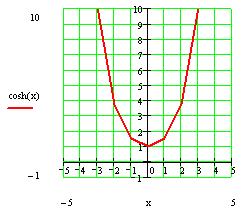
Рис. 4.
Гиперболические тангенс и котангенс определяются через отношение гиперболического синус и косинуса.
Гиперболического тангенсом называется функция
,
.
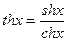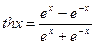Основные свойства гиперболического тангенса.
1. Область определения: .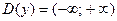
2. Множество значений: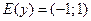 
.
3. Четность и нечетность: нечётная.
4. Периодичность: не периодическая.
5. Нули функции: .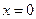
6. Промежутки знакопостоянства:функция отрицательна для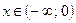 
; положительна – для 
.
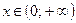7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.
8. Промежутки возрастания и убывания: функция возрастает для .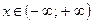
9. Точки пересечения с осями координат: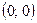 
.
10. Асимптоты: имеет горизонтальные асимптоты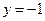 
и .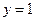
11. График функции изображен на рисунке 5.
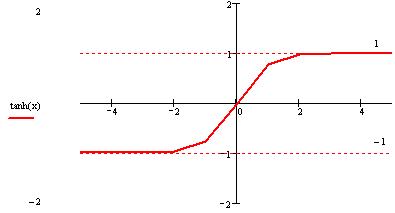
Рис. 5.
Гиперболический котангенсом называется функция
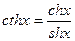, т.е.
.
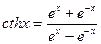