Решение задач муниципального этапа
Решение задач муниципального этапа
Всероссийской олимпиады школьников по математике
Класс
1. Постройте ромб по диагонали и его высоте
Решение:Сначала построить треугольник по гипотенузе, равной диагонали, и катету, равному высоте. По этому треугольнику построить искомый ромб.
2. Расстояние между пунктами А и В – 60 км. Из А в В выходит автомобиль, а из В в том же направлении одновременно с первым автомобилем выходит второй. Если скорость первого автомобиля увеличить на 10 км/ч, а второго – на 8 км/ч, то первый автомобиль догонит второй в том же месте, но на час раньше. Какова скорость каждого автомобиля?
 Решение:Пусть х км/ч скорость первого автомобиля, а у км/ч – скорость второго. Тогда
Решение:Пусть х км/ч скорость первого автомобиля, а у км/ч – скорость второго. Тогда 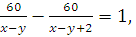 откуда x-y=10. Значит х
откуда x-y=10. Значит х 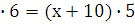 , х=50, у=40. Ответ: 50 и 40 км/ч
, х=50, у=40. Ответ: 50 и 40 км/ч
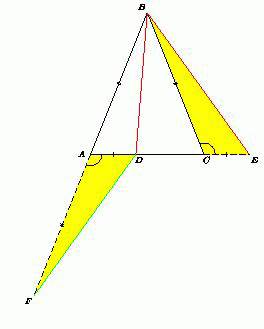
3. В равнобедренном треугольнике АВС (АС=АВ) отношение высоты AD к основанию ВС равно 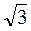 . Точка М взята на стороне АВ так, что
. Точка М взята на стороне АВ так, что 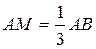 . Найти величину угла МСВ.
. Найти величину угла МСВ.
Решение:Проведем DF║CM. Так как CD=DB, то MF=FB, а с учетом 
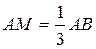 получаем AM=MF. Отсюда DE=AE.
получаем AM=MF. Отсюда DE=AE. 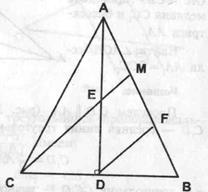 Имеем
Имеем 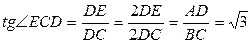 . Следовательно,
. Следовательно, 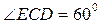 .
.
4. Вычислите 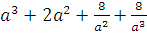 , если
, если 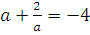 .
.
Решение: 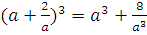 +6(
+6( 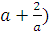 =-64, тогда
=-64, тогда 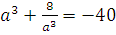 ;
;
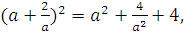 тогда
тогда 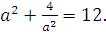
Получаем 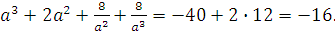
5. Три юноши и семь девушек отправляются на двух лодках по реке. Сколькими способами их можно разместить в лодках поровну, чтобы в каждой лодке был хотя бы один юноша?
Решение:
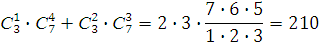
Решение задач муниципального этапа
Всероссийской олимпиады школьников по математике
Класс
1. Найдите наибольшее значение функции у=(2-х)(х+2).
Ответ:4
2. Натуральное число х возвели в третью степень. Докажите, что хотя бы одно из чисел 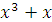 или
или 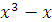 делится на 10.
делится на 10.
Решение: Возможное решение. Найдем последнюю цифру выражений 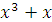 и
и 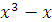 :
:
| x оканчивается на | ||||||||||
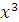 оканчивается на оканчивается на | ||||||||||
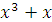 оканчивается на оканчивается на | ||||||||||
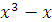 оканчивается на оканчивается на |
Из таблицы видно, что хотя бы одно из чисел 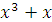 или
или 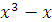 делится на 10.
делится на 10.
3. На боковой стороне АВ равнобедренного треугольника как на диаметре построена окружность. Окружность пересекает основание АС в точке М и боковую сторону ВС в точке N. Найдите длины отрезков MN и NC, если AC=a и AB=b. 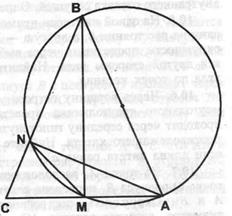
Решение: Так как АВ – диаметр окружности, то 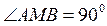 . Тогда ВМ – высота равнобедренного треугольника. Отсюда
. Тогда ВМ – высота равнобедренного треугольника. Отсюда 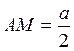 ,
, 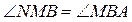 . Следовательно,
. Следовательно, 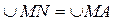 и
и 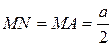 . Имеем:
. Имеем: 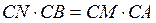 . Отсюда
. Отсюда 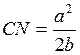 .
.
4. Сколько членов арифметической прогрессии нужно взять, чтобы их сумма равнялась -122,5, если первый член прогрессии – наименьшее целое число, удовлетворяющее неравенству 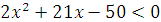 , а разность прогрессии – большее из чисел 0,5 и
, а разность прогрессии – большее из чисел 0,5 и 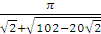 ?
?
Решение:
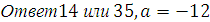 , d=0,5.
, d=0,5.
5. Сколько различных пятизначных чисел, делящихся на 4 можно составить из цифр 1,2,3 и 5?
Решение:Указанные числа должны оканчиваться на 12, 32 или 52.При каждой из таких возможностей на первых трех местах может стоять любая из данных четырех цифр. Это размещения с повторениями. Их будет 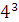 . Всего чисел 64
. Всего чисел 64 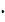 3=192.
3=192.
Решение задач муниципального этапа
