Плоскости частного положения
Лекция 2
Взаимное положение прямой и плоскости, двух плоскостей на эпюре Монжа
1. Определение плоскости на эпюре Монжа.
2. Прямые и точки на плоскости.
3. Главные линии плоскости.
4. Плоскости частного положения.
5. Параллельность и перпендикулярность прямой и плоскости.
6. Пересечение двух плоскостей.
Определение плоскости на эпюре Монжа.
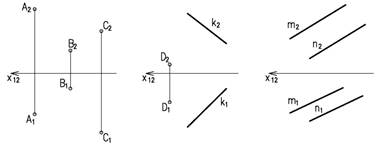
 Положение плоскости в пространстве определяется тремя не лежащими на одной прямой точками, прямой и не лежащей на ней точкой, двумя параллельными или пересекающимися прямыми, плоской фигурой. Примеры задания плоскости даны на рисунке 1.1.
Положение плоскости в пространстве определяется тремя не лежащими на одной прямой точками, прямой и не лежащей на ней точкой, двумя параллельными или пересекающимися прямыми, плоской фигурой. Примеры задания плоскости даны на рисунке 1.1.
Рисунок 1.1
Все изображенные на рисунке 1.1 плоскости являются плоскостями общего положения. Плоскостью общего положенияназывается плоскость не перпендикулярная и не параллельная ни одной из плоскостей проекций.
Прямые и точки в плоскости
Точка лежит в плоскости, если она лежит на прямой принадлежащей этой плоскости. Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости.
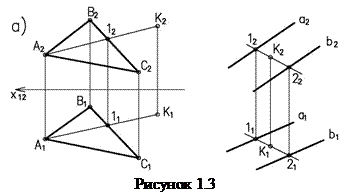 б)
б)
На рисунке 1.3а. фронтальная проекция точки К выбрана произвольно в плоскости  (DАВС). Для построения горизонтальной проекции через К2 проведена произвольная прямая проходящая через точки 12 и А2 принадлежащие плоскости
(DАВС). Для построения горизонтальной проекции через К2 проведена произвольная прямая проходящая через точки 12 и А2 принадлежащие плоскости  . Построив горизонтальные проекции точки 11 проведем горизонтальную проекцию прямой принадлежащей плоскости
. Построив горизонтальные проекции точки 11 проведем горизонтальную проекцию прямой принадлежащей плоскости  и по линии связи найдем на ней горизонтальную проекцию К1. Аналогично построена точка К принадлежащая плоскости g (a||b) (рисунок 1.3б).
и по линии связи найдем на ней горизонтальную проекцию К1. Аналогично построена точка К принадлежащая плоскости g (a||b) (рисунок 1.3б).
Главные линии плоскости
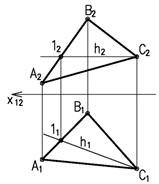
Главными линиями плоскости называются ее горизонтали, фронтали и линии наибольшего ската. Горизонтали плоскости – это прямые, принадлежащие плоскости и параллельные горизонтальной плоскости проекций – h (h1, h2) .
Все горизонтали плоскости параллельны между собой. Фронтальные проекции горизонталей параллельны оси Х12 (рисунок 1.4).

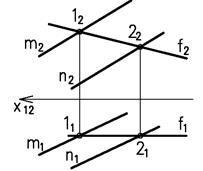
Фронтали плоскости – это прямые, принадлежащие плоскости и параллельны фронтальной плоскости проекций – f (f1, f2).
Все фронтали плоскости параллельны между собой. Горизонтальные проекции фронталей параллельны оси Х12 (рисунок 1.5).

Плоскости частного положения
Плоскости, как и прямые, относительно плоскостей проекций могут занимать частное положение. Плоскости, перпендикулярные или параллельные одной из плоскостей проекций, называются плоскостямичастного положения.Плоскости, перпендикулярные одной из плоскостей проекций, называютсяпроецирующими(рисунок 1.6).
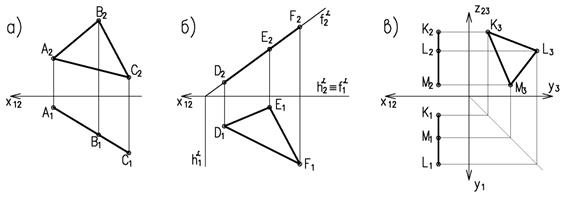

а) горизонтально проецирующая плоскость 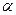 (DАВС);
(DАВС);
б) фронтально проецирующая плоскость d (D DEF);
в) профильно-проецирующая плоскость q (D KLM).
 Плоскости, параллельные одной из плоскостей проекций, называются плоскостями уровня(рисунок 1.7).
Плоскости, параллельные одной из плоскостей проекций, называются плоскостями уровня(рисунок 1.7).

а) горизонтальная плоскость уровня β, заданная треугольником АВС;
б) фронтальная плоскость уровня ε заданная пересекающимися прямыми mn;
в) профильная плоскость уровня g, заданная треугольником KLM
