Нелинейные корректирующие звенья.
Нелинейные корректирующие звенья бывают двух типов: нелинейные корректирующие звенья, включаемые последовательно или параллельно с основными звеньями системы, и переключающие корректирующие звенья, релейно изменяющие настройку или структурную схему системы при соответствующем изменении ее состояния или внешних условий. Последний тип корректирующих звеньев присущ только нелинейной коррекции.
В качестве нелинейных корректирующих звеньев применяются нелинейные звенья непрерывного и дискретного действия, их комбинации друг с другом, а также с линейными корректирующими звеньями.
Простейшим видом нелинейных корректирующих звеньев являются корректирующие звенья с нелинейными статическими характеристиками. Первая область их применения, как уже говорилось, - это коррекция статических характеристик системы и, в частности, коррекция нежелательных нелинейностей ее основных звеньев. Вторая область применения – это коррекция динамических свойств. В этом случае такие безынерционные корректирующие звенья часто применяются в комбинации с линейными корректирующими звеньями, образуя вместе нелинейные динамические корректирующие звенья.
В качестве нелинейных статических характеристик используют при этом характеристики с насыщением, зоной нечувствительности, петлевые, а также различные специально подобранные нелинейности. Если пользоваться частотным описанием таких нелинейных динамических корректирующих звеньев (на основе гармонической линеаризации), то их назначение можно определить следующим образом. Во-первых, они применяются для получения определенной желаемой зависимости частотных характеристик от амплитуды сигнала и тем самым для получения различной реакции системы на воздействия разной величины или, наоборот, для устранения нежелательных таких зависимостей, обусловленных имеющимися в системе нелинейностями основных звеньев. Во-вторых, такие корректирующие звенья применяются для преодоления той жесткой зависимости между амплитудной и фазовой частотными характеристиками, которая существует в линейных системах, с целью независимой корректировки каждой из этих характеристик. Для последней цели часто используются так называемые псевдолинейные корректирующие звенья.

Рис.12.5. Структурная схема нелинейного динамического корректирующего звена.
На рис. 12.5 в качестве примера показана структурная схема нелинейного динамического корректирующего звена, состоящего из двух линейных корректирующих звеньев 1 и 3 и нелинейного звена с насыщением 2. При  звено 1 является обычным пропорционально-дифференцирующим звеном, т. е. фильтром верхних частот, а звено 3 - соответственно инерционным звеном, т. е. фильтром нижних частот. Для малых входных сигналов, когда нелинейное звено 2 не входит в насыщение, передаточная функция всей схемы равна 1, т. е. это звено не влияет на работу системы, в которой находится. При достаточно больших сигналах, когда звено 2 входит в насыщение, схема ведет себя как динамическое звено со спадающей с ростом частоты амплитудной частотной характеристикой, степень спадания которой зависит от величины входного сигнала, и с примерно постоянным фазовым сдвигом.
звено 1 является обычным пропорционально-дифференцирующим звеном, т. е. фильтром верхних частот, а звено 3 - соответственно инерционным звеном, т. е. фильтром нижних частот. Для малых входных сигналов, когда нелинейное звено 2 не входит в насыщение, передаточная функция всей схемы равна 1, т. е. это звено не влияет на работу системы, в которой находится. При достаточно больших сигналах, когда звено 2 входит в насыщение, схема ведет себя как динамическое звено со спадающей с ростом частоты амплитудной частотной характеристикой, степень спадания которой зависит от величины входного сигнала, и с примерно постоянным фазовым сдвигом.
Такое корректирующее звено применяется в качестве последовательного корректирующего звена, например, для устранения автоколебаний при больших возмущениях и соответствующего увеличения критического по устойчивости значения коэффициента передачи системы. Это корректирующее звено применяется также в цепях обратной связи, например, следящих систем для улучшения качества переходных процессов при больших входных сигналах.
Псевдолинейные корректирующие звенья – это нелинейные корректирующие звенья, эквивалентные амплитудные и фазовые частотные характеристики которых не зависят от амплитуды входного сигнала, чем и объясняется их название. Как уже говорилось, основным свойством этой группы корректирующих звеньев является практическое отсутствие связи между эквивалентными амплитудной и фазовой частотными характеристиками.
Существуют два основных типа псевдолинейных корректирующих звеньев: фильтры с амплитудным ослаблением - для коррекции амплитудной характеристики без изменения фазы и фильтры с фазовым опережением - для коррекции фазовой характеристики без изменения амплитудной характеристики.
На рис. 12.6 показан пример схемы фильтра с амплитудным ослаблением. Здесь звено 1 - реле, 2 - фильтр нижних частот ФНЧ, звено 3 дает абсолютное значение (модуль) входного сигнала Х1 (в электрических системах постоянного тока это выпрямительная схема), 4 – множительное звено.
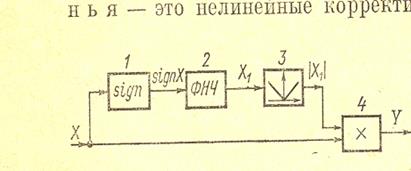
Рис.12.6. Схема нелинейного фильтра с амплитудным ослаблением.
Существует много других псевдолинейных корректирующих устройств. Имеются, например, псевдолинейные интегрирующие звенья, амплитудная характеристика которых совпадает с амплитудной характеристикой обычнoгo линейного интегрирующего звена, а фазовый сдвиг вдвое меньше, что облегчает задачу стабилизации астатических систем с таким интегрирующим звеном. Предложены псевдолинейные дифференцирующие звенья, обладающие характеристиками, более близкими к характеристикам идеального дифференцирующего звена, чем у реальных линейных дифференцирующих звеньев.
Сложные нелинейные динамические корректирующие звенья получаются в результате синтеза оптимальных САУ. Они включают, помимо функциональных зависимостей, логические операции и зачастую требуют для своей реализации специального вычислительного устройства.
Переключающие корректирующие звенья осуществляют коррекцию динамических свойств системы путем дискретных изменений ее параметров и структурной схемы в ходе процесса управления в функции переменных системы и внешних воздействий. Эти изменения могут осуществляться как в основных, так и в корректирующих звеньях системы.
Примером такой коррекции является релейная форсировка переходных процессов в системах с насыщением, которая осуществляется при больших отклонениях от заданного режима путем дискретного изменения настройки корректирующих звеньев системы.
Переключающие корректирующие звенья применяются также для изменения алгоритма работы управляющего устройства системы при значительных изменениях внешних условий или свойств самой системы. Системы с такой коррекцией относятся к простейшим самоорганизующимся САУ.
В системах, управляющее устройство которых включает в себя вычислительную машину, реализующую алгоритм управления, переключающие корректирующие звенья часто также могут быть реализованы алгоритмически в этой ЭВМ без создания их физически в виде отдельного функционального блока.
Изложенное показывает большие возможности нелинейной коррекции. Вместе с тем, говоря о достоинствах нелинейной коррекции, следует отметить, что такая коррекция по своей природе является более специализированной по отношению к режимам системы, при которых она дает нужный эффект. Может получиться, например, так, что нелинейная коррекция, выбранная для определенного вида внешних воздействий, окажется не только неэффективной, но даже вредной при других неучтенных режимах САУ. Поэтому, чем шире диапазон внешних воздействий и вообще условий работы системы, тем труднее выбрать нелинейную коррекцию и тем скорее может оказаться наиболее приемлемой линейная коррекция. Последнее обстоятельство усугубляется тем, что, к сожалению, не существует какой-либо общей методики выбора нелинейных корректирующих звеньев и практически при синтезе приходится прибегать к методу проб и последовательных приближений, используя опыт и известные рекомендации по применению отдельных частных приемов и схем нелинейной коррекции.
