Раздел 1. Матрицы, определители, системы линейных уравнений.

Лекция 1.1. Числовые матрицы и действия над ними.

Краткое содержание: Место линейной алгебры и аналитической геометрии в естествознании. Роль отечественных ученых в развитии этих наук. Понятие матрицы. Операции над матрицами и их свойства.

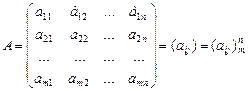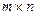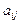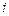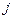Таблица чисел вида называется прямоугольной матрицей размерности . Матрицы обозначаются заглавными латинскими буквами A, B, C,…Числа, из которых состоит таблица, называют элементами матрицы. Каждый элемент имеет два индекса и , обозначающие соответственно номер строки ( 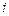) и номер столбца( 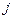), в которых расположен данный элемент. Используются следующие обозначения матрицы .

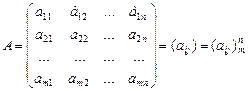Две матрицы называются равными, если они имеют одинаковую размерность (т.е. одинаковое число строк и столбцов) и если числа, стоящие на соответствующих местах этих матриц, равны.

Если число строк матрицы равно числу ее столбцов, матрицу называют квадратной. В квадратной матрице число строк (или столбцов) называют порядком матрицы. В частности квадратная матрица первого порядка – это просто действительное число. Соответственно говорят, что вектор строка 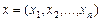есть матрица размерности 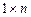, а вектор-столбец 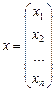имеет размерность .

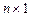Элементы, стоящие на главной диагонали квадратной матрицы (идущей из левого верхнего в правый нижний угол), называются диагональными.

Квадратная матрица все элементы которой не лежащие на главной диагонали равны 0 называется диагональной.

Диагональная матрица, все диагональные элементы которой равны 1, а все внедиагональные – 0, называется единичной и обозначается 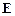или 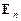, где n- ее порядок.

Основные операции над матрицами – сложение матриц и умножение матрицы на число.

Произведением матрицы А на число 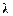называется матрица той же размерности, что и матрица А, каждый элемент которой умножен на это число .

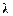Например: ; .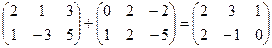

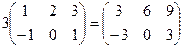Свойства операции умножения матрицы на число:

1. l(mА)=(lm)А (ассоциативность)

2. l(А+В)= lА+lВ (дистрибутивность относительно сложения матриц)

3. (l+m)А=)=lА+mА (дистрибутивность относительно сложения чисел)

Линейной комбинацией матриц А и В одинакового размера называется выражение вида: aА+bВ, где a,b - произвольные числа

Суммой матрицА и В ( это действие применимо только к матрицам одинаковой размерности) называется матрица С такой же размерности, элементы которой равны суммам соответствующих элементов матриц А и В.

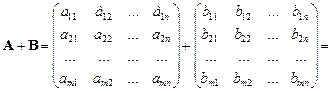
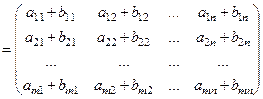
Свойства сложения матриц:

1)А+В=В+А(коммутативность)

2)(А+В)+С=А+(В+С)=А+В+С(ассоциативность)

Разностью матрицА и В ( это действие применимо только к матрицам одинаковой размерности) называется матрица С такой же размерности, элементы которой равны разности соответствующих элементов матриц А и В.

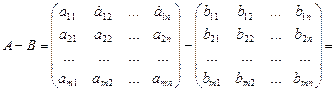
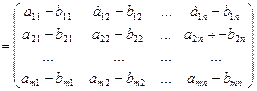
Транспонирование. Если элементы каждой строки матрица 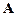размерности 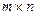записать в том же порядке в столбцы новой матрицы, причем номер столбца будет равен номеру строки, то новую матрицу называют транспонированной по отношению к 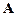и обозначают 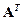. Размерность 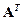равна 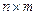Переход от 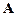к 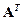называется транспонированием. Ясно так же, что . ,

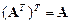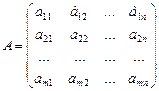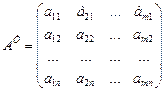
Умножение матриц. Операция умножения матриц возможна лишь в том случае, если число столбцов первого множителя равны числу строк второго. В результате умножения получим матрицу, число строк которой совпадает с числом строк первого множителя, а число столбцов с числом столбцов второго: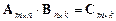

Правило умножения матриц: чтобы получить элемент, стоящий в 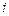–й строке и 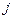–м столбце произведения двух матриц, нужно элементы 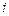–й строки первой матрицы умножить на элементы 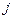–го столбца второй матрицы и полученные произведения сложить. На математическом жаргоне иногда говорят: нужно 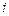–ую строку матрицы 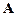умножить на 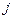–й столбец матрицы 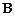. Ясно, что строка первой и столбец второй матрицы должны содержать одинаковое количество элементов.

В отличие от этих операций операция умножения матрицы на матрицу определяется более сложно. Пусть заданы две матрицы А и В, причем число столбцов первой из них равно числу строк второй: например, матрица А имеет размерность 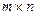, а матрица В – размерность 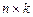. Если

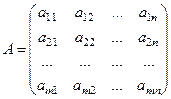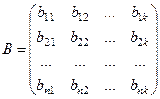, , то матрица размерности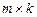

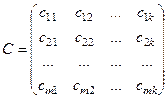, где 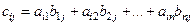(i=1,…,m;j=1,…,k)

называется произведением матрицы А на матрицу В и обозначается АВ.

ПР.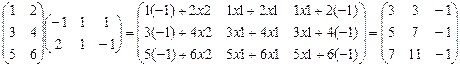

Свойства операции умножения матриц:

1. (АВ)С=А(ВС)=АВС(ассоциативность)

2. (А+В)С=АС+ВС (дистрибутивность)

3. А(В+С)=АВ+А(дистрибутивность)

4. Умножение матриц некоммутативно: АВ не равно ВА., если равно, то эти матрицы называются перестановочными.

Элементарные преобразования над матрицами:

1. Перемена местами двух строк (столбцов)

2. Умножение строки (столбца) на число, отличное от нуля

3. Прибавление к элементам одной строки (столбца) элементов другой строки (столбца), умноженных на какое либо число

Лекция 1.2. Определители с действительными коэффициентами. Нахождение обратной матрицы.

Краткое содержание: Определители и их свойства. Методы вычисления определителей с действительными коэффициентами. Нахождение обратной матрицы дляматриц третьего порядка.

Понятие определителя вводится только для квадратной матрицы. Определитель – это число, которое находится по вполне определенным правилам и обозначается 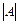или det A.

Определитель матрицы второго порядка находится так: 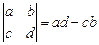или

Определителем третьего порядка называется число:

.

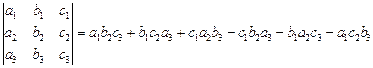Для запоминания этой громоздкой формулы существует «правило треугольников»:

Определитель третьего порядка можно посчитать и другим методом ‑ методом разложения по строке или по столбцу. Введем некоторые определения:

Минором 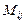квадратной матрицы А называется определитель матрицы А, который получается вычеркиванием 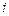–й строки и 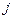–го столбца: например для 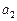минор - .

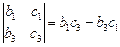Алгебраическим дополнением 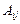элемента определителя называется его минор, взятый со своим знаком, если сумма номеров строки и столбца, в которых расположен элемент, четна, и с обратным знаком, если сумма номеров нечетна: .

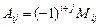Тогда: Определитель третьего порядка равен сумме произведений элементов какого-нибудь столбца (строки) на их алгебраические дополнения.

ПР: Вычислим определитель: 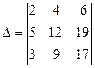, разложив его по элементам первой строки.

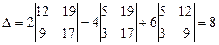
Свойства определителей:

1.Определитель равен 0, если содержит две одинаковые строки (столбца) или нулевую строку (столбец).

2.Определитель меняет свой знак при перестановке двух строк (столбцов).

3.Общий множитель в строке (в столбце) можно выносить за знак определителя.

4.Определитель не меняется, если к строке (столбцу) прибавить любую другую строку (другой столбец), умноженную на произвольное число.

5.Определитель не меняется при транспонировании матрицы .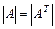

6.Определитель еденичной матрицы равен 1: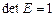

7.Определитель произведения матриц равен произведению определителей

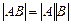
Обратная матрица.

Квадратная матрица называется невырожденной, если ее определитель отличен от нуля.

Если при умножении квадратных матриц А и В в любом порядке получается единичная матрица (АВ=ВА=Е), то матрица В называется обратной матрицей для матрицы А и обозначается 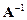, т.е. .

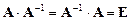Теорема.Всякая невырожденная матрица имеет обратную.

Алгоритм нахождения обратной матрицы: