Понятие продуктивной функции

Распределение n разных предметов по k урнам

Количество размещений по k урнам n разных предметов при условии, что в первую урну попало 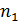предметов, во вторую – 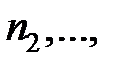в последнюю – 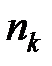предметов, равно , .

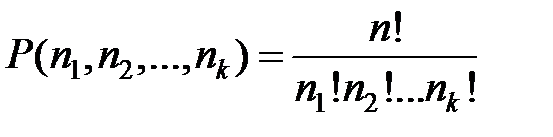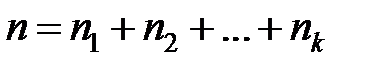Распределение n одинаковых предметов по k урнам

Установим, что n одинаковых предметов между k урнами можно разделить 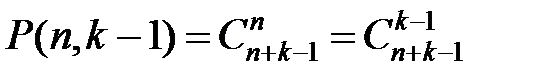способами.

Количество искомых распределений n одинаковых предметов между 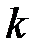урнами равняется количеству перестановок из 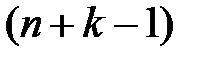предметов с повторениями 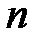предметов первого типа и 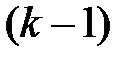предметов второго типа, т.е. равно .

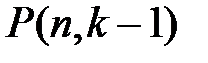Если делить справедливо, с уровнем справедливости 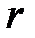, то каждый участок распределения должен получать минимум 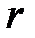предметов. Тогда сначала раздадим каждому по 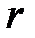предметов. После чего остается 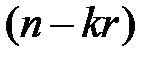предметов, которые и распределим по усмотрению. Это можно сделать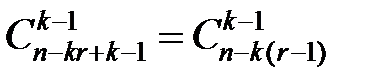

способами.

Распределение разных предметов без учета порядка предметов по урнам

Нужно разделить n разных предметов по 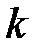урнам, емкость которых не ограничена. Первый предмет можно положить в любую из 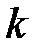урн, второй(независимо от первого), тоже в 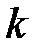урн и т.д. По правилу произведения предметы можно разделить 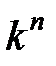способами.

Распределение разных предметов с учетом их порядка в урнах

Если не ограничивать количество предметов в урнах и если предметы не разнятся между собой, то количество таких распределений равно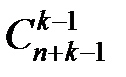

Каждому способу разделения одинаковых предметов между урнами соответствует 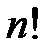способов распределения разных предметов с учетом их порядка, которые получаются с помощью перестановок предметов между собой без изменения количества предметов в урнах. По правилу умножения получаем искомое количество распределений .

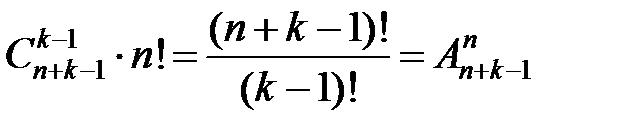Распределение разных предметов между одинаковыми урнами при условии, что урны не пусты

Обозначим 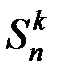количество способов разделения n разных предметов между 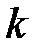одинаковыми урнами так, чтобы каждая урна была не пустой. Из каждого такого распределения можно получить 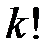аналоговых распределений по разным урнам. Таким образом, количество 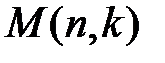распределений 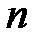разных предметов между 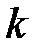разными урнами с использованием каждой урны в каждом распределении (не пустых урн) равно 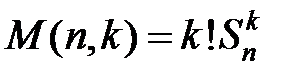(5.15).

Числа Моргана

Число 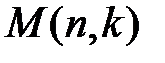носят название чисел Моргана.

Формула 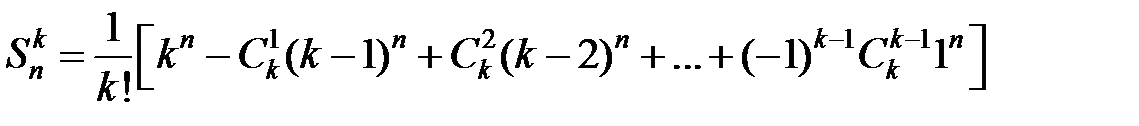выплывает из формулы включений и исключений.

41. Композиції і розбиття.

Определение. Композицией числа 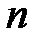называется всякое представление 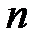в виде упорядоченной суммы целых положительных чисел.

Определение. Разбиением числа 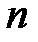называется всякое представление 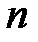в виде неупорядоченной суммы целых положительных чисел.

42. Підходи до вивчення комбінаторних об’єктів і чисел. Поняття про продуктивні функції. Поняття про рекурентні співвідношення.

Понятие продуктивной функции

Пусть задана некоторая последовательность чисел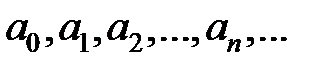

Определение. Если степенной ряд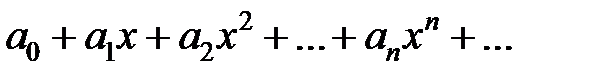

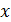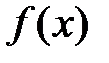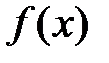совпадает при некоторых с функцией , то называется продуктивной функциейдля последовательности .

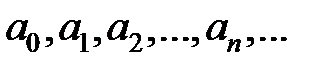Рекуррентное соотношение -это соотношение(равенство, система равентсв) позволяющее свести решение комбинационной задачи для некоторого числа предметов к аналогичной задаче с меньшей размерностью. Решение комбинационных задач с помощью рекуррентных соотношений - это метод рекуррентных соотношений.

43. Метод продуктивних функцій. Продуктивні функції сполучень. Продуктивні функції розміщень та перестановок. Продуктивні функції для розбиття чисел.

Пусть дана некая последовательность чисел а₀, а₁, а₂…., a_n… Если степенной ряд а₀₊а₁х+а₂х²+….a_n хⁿ+… совпадает при некоторых х с функцией f(x), то f(x) называют продуктивной функцией для последовательности а₀, а₁, а₂…., a_n…

44. Метод рекурентних співвідношень. Числа Фібоначчі. См вопр. 42

Числа Фиббоначчи – элементы последовательности, в которой каждое последующее числоравно сумме двух предыдущих чисел.

45. Основи теорії кодування. Алфавітне кодування. Кодування з мінімальною надлишковістю. Алгоритм Фано. Алгоритм Хаффмена. Завадостійке кодування. Стиснення даних. Криптографія.

46. Зародження теорії графів як математичної дисципліни. Типові задачі теорії графів. Походження графів.

– ­­­­­Леонардо Ейлер(1735р, Ейлеров цикл(містить всі ребра графа)), загадка про кенігсберзькі мости.

– Кіргоф(1843р) – граф ланцюга, розробив алгоритм знаходження дерев.

– Келі(1857р) – задача перелічення всіх дерев зі степенями вершин 1 і 4.

– Гамільтон(1859р) – частковий випадок задачі про комівояжера(граф додекаедра; простий цикл, що містить всі вершини графа – гамільтонів цикл).

– Хівуд(1890р) – проблема 4 фарб, довів що достатньо 5.

– Л.С. Понтрягін(1927р) – виявив топологічний критерій планарнсті. – К.Курятовський(1930р).

– с 30х рр. ХІХ ст.. популярність графів зростає.

Задачі:загадка про кенігсберзькі мости, задача перелічення всіх дерев зі степенями вершин 1 і 4, задача комівояжера(посетить все пункти только 1 раз, найкоротший путь, повертається в початок), проблема 4 фарб(розфарбування країн у різні фарбі з сусідніми).

47. Визначення графів. Різновиди графів. Неорієнтовані та орієнтовані графи. Основні терміни для неорієнтованих та орієнтованих графів.

Граф – упорядоченная пара множества вершин и множества ребер(пар вершин).

Графы делятся на ориентированные и неориетированные, а также:
– Пустой – множества ребер пустое.;

– Простой – нет петель и паралельных ребер;

– Полный – простой и каждая пара вершин смежная.

– Регулярным/однородным – степени всех вершин одинаковы.

– Дерево – нет циклов и граф связный.

– Мультиграф – есть паралельные ребра.

– Псевдограф – есть петли и кратные(паралельные) ребра.

Термины:Смежные вершины, смежные ребра, инцидентные ребра и вершины, параллельные(кратные) ребра, маршрут, длина маршрута(кол-во ребер), замкнений маршрут, цепь(все ребра разные), простая цепь(все вершины, кроме конца/начала разные), цикл,подграф, компонента связности(макс. связный подграф), точка сочленения графа, диаметр,грань(коморка), граница грани, эксцентриситет(самое большое растояние от вершины а), радиус(самый маленький эксцентриситет), центр графа(вершины с наймешим эксц-м).

48. Способи задання графів. Геометрична реалізація графів. Матриця суміжності. Матриця інциденцій. Число вершин і ребер графа.

Способы: вербльный, аналитический, матричный, графический.

Матрица смежности – смежность вершин, колво ребер.

Матрица инцидентности – инцидентность вершин/ребер.

Сумма степенем неорграфа равна удвоеному кол-ву его ребер.

49. Операції над графами. Операції вилучення ребер та вершин. Операція введення ребра, операція введення вершини у ребро. Операція об’єднання графів. Операції додавання і множення графів.

Удаление ребра, удаление вершины(и инцидентных ей ребер), введение ребра и введение вершины, обьединение графов(ассоциативность, комутативность), дизъюнкитвное объединение(разные вершины), пересечение, соединение(сильное произведение), композиція, декартовое произведение,

50. Ізоморфізм графів. Підграфи. Алгебраїчний критерій ізоморфізму графів. Зв'язок з відношеннями. Ізоморфізм як відношення еквівалентності.

Изоморфизм графов – отношение эквивалентности.

51. Плоскі та планарні графи. Гомеоморфні графи. Теорема Понтрягіна-Куратовського. Теорема Жордана. Жорданова крива. Побудова плоского зображення графа.

Плоский граф – граф нарисованный без пересечений(только в вершинах есть).

Граф планарен, если его можно нарисовать без пересечений(изоморфен плоскому графу).

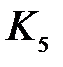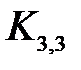Теорема Понтрягина – Куратовского гласит: граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных и , где 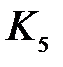– полный 5-вершинный граф, а 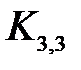– полный двудольный граф, каждая доля которого состоит из 3 вершин.

Теорема Жордана: Если 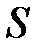замкнутая жорданова кривая, то всякая жорданова кривая, соединяющая точки 1 и 2, лежащие на 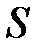, либо полностью лежит внутри 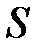, либо вне 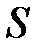, либо пересекает 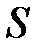в одной единственной точке отличной от 1 и 2.

Жордановой кривойна плоскости называется непрерывная кривая линия без самопересечений. Замкнутая жорданова кривая – это жорданова кривая, начало и конец которой совпадают.

Для плоской укладки графа и попутной проверки, планарный ли он, удобно пользоваться гамма-алгоритмом.

На вход подаются графы, обладающие следующими свойствами:

1. Граф связный.

2. Граф имеет хотя бы один цикл.

3. Граф не имеет мостов, т. е. ребер, после удаления которых граф распадается на две компоненты связности.

Гамма-алгоритм (в общем виде)

1. (Инициализация). Выберем любой простой цикл исходного графа ; изобразим его на плоскости в виде грани, которую примем за уже уложенную часть ; сформируем сегменты ; если множество сегментов пусто, то перейти к п. 3.

2. (Общий шаг). Пока множество сегментов непустое:

a. Для каждого сегмента найти множество . Если существует сегмент , для которого , то граф не планарный, конец.

b. Выбираем один из сегментов с минимальным числом, вмещающих его граней.

c. Выбираем одну из подходящих граней для выбранного сегмента.

d. В данном сегменте выбираем цепь между двумя контактными вершинами и укладываем ее в выбранной грани. Учтем изменения в структуре сегментов и перейдем к п. a).

3. (Завершение). Построена плоская укладка исходного графа , конец.

52. Зв'язність графів. Ейлерові та гамільтонові графи. Поняття зв'язності графів, компонента зв'язності, n-зв'язний граф. Властивості зв'язних графів. Метричні характеристики зв'язних графів.

Две вершины 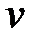и 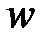в графе связны, если существует соединяющая их (простая) цепь. Если же в графе нет ни одной цепи, соединяющей вершины 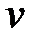и 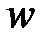, то вершины 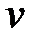и 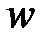являются несвязными.

Граф называется связным, если любая пара его вершин связана. Если же в графе имеется хотя бы одна пара вершин, не соединенных цепью, то граф называется несвязным.

Эйлеров цикл (эйлерова линия, замкнутая эйлерова цепь, эйлерова цепь) – это цикл, содержащий все ребра графа. – Эйлеров граф(уникурсальный)

Гамильтонов граф – это граф, содержащий гамильтонов цикл(все вершины проходяться только 1 раз, задача комивояжера).

Классы эквивалентности(множество связных вершин), из которых состоит несвязный граф, называются его компонентами. Между разными компонентами связности ребер нет.

Любой связный граф состоит из одной компоненты связности – всего графа.

Граф называется n-связным, если между любыми его двумя вершинами найдется 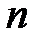цепей, попарно не имеющих общих неконцевых вершин.

Свойства связных графов

1. Связный граф остается связным после удаления ребра тогда и только тогда, когда это ребро содержится в цикле.

2. Связный граф, имеющий 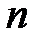вершин, содержит по крайней мере 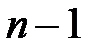ребро.

3. В связном графе любые две простые цепи максимальной длины имеют по крайней мере одну общую вершину.

4. Пусть у графа 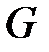есть 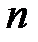вершин. Пусть 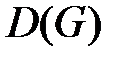– минимальная из степеней вершин этого графа. Тогда .

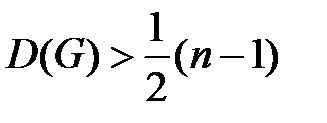Метрические хар-ки:расстояние, диаметр, эксцентриситет, грань, граница грани.

53. Ейлерові графи. Теорема Ейлера. Алгоритм знаходження ейлерова цикла (теорема Флері).

Теорема (формула Эйлера). Количество граней в любой плоской укладке планарного графа, имеющего 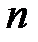вершин, 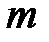ребер и 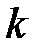компонент связности, равно .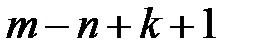